Вопросы по математике:

1)Матрицы и действия над ними

Определения.

Матрицей называется прямоугольная  таблица чисел  или буквенных выражений, содержащая m строк и n столбцов:

,

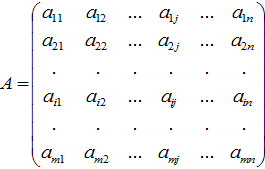  называют  элементами  матрицы.

Матрица, у которой число строк равно числу столбцов, т.е. m=n, называется квадратной матрицей, а число n называется порядком матрицы:

A =  

 Элементы   образуют главную диагональ квадратной матрицы. Если все элементы квадратной матрицы, расположенные вне главной диагонали, равны нулю, то матрицу называют диагональной. Если в диагональной матрице все элементы главной диагонали равны между собой, то ее называют скалярной.

Если в скалярной матрице все элементы главной диагонали равны единице, то матрицу называют единичной и обозначают буквой E .

Если все элементы матрицы  равны  0, то матрица называется нулевой и ее обозначают буквой O.

Две матрицы считаются равными, если они одинакового размера, и элементы, стоящие на пересечении строк и столбцов с одинаковыми номерами, равны, т.е. если

 

Сложение матриц.

Суммой матриц одной и той же размерности называется матрица размерности , каждый элемент которой представляет собой сумму соответствующих элементов матриц A и B:

Матрицы разных размерностей складывать нельзя.

Пример1. .

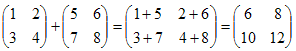Свойства сложения матриц. 1. Коммутативность. A+B=B+A 2. Ассоциативность. (A+B)+C=A+(B+C)

Умножение матриц, транспонирование матриц.

Матрица C, элементы которой с_ij равны элементам матрицы A, умноженным на число α, называют произведением матрицы A на α:

Пример 2. .

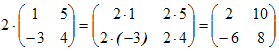Произведением матрицы размерности на матрицу размерности называется матрица размерности , где:

Произведение матриц существует только тогда, когда число столбцов первой матрицы равно числу строк второй матрицы.

Пример 3.

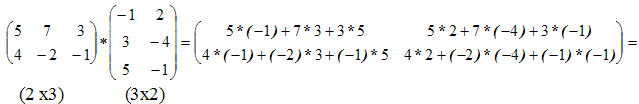
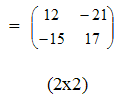
Пример 4.

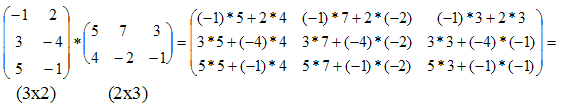
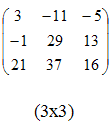
Результатом транспонирования матрицы размерности является матрица размерности , где

Пример 5.  

Свойства транспонированных матриц.

1). Если E-единичная матрица, то E=E^T.

2). Двукратное транспонирование не изменяет матрицу (A^T)^T=A.

3). Транспонирование суммы матриц равносильно сложению транспонированных матриц: (A+B)^T=A^T+B^T

4).Транспонирование произведения матриц равносильно умножению транспонированных матриц: .

5). Транспонирование обратной матрицы равносильно вычислению обратной к транспонированной матрице: (A^-1)^T=(A^T)^-1 .

6). Если транспонированная матрица A^T совпадает с данной матрицей A, то матрица A называется симметрической.

2)Определитель матрицы

Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца. Определение через разложение по первой строке

Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:

Для матрицы детерминант определяется как

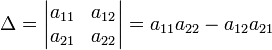
Для матрицы определитель задаётся рекурсивно:

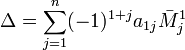,    где  — дополнительный минор к элементу a_1j. Эта формула называется разложением по строке.

В частности, формула вычисления определителя матрицы такова:

= a₁₁a₂₂a₃₃ − a₁₁a₂₃a₃₂ − a₁₂a₂₁a₃₃ + a₁₂a₂₃a₃₁ + a₁₃a₂₁a₃₂ − a₁₃a₂₂a₃₁

Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке):

Также справедливо и аналогичное разложение по любой строке (столбцу):

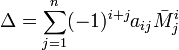
Обобщением вышеуказанных формул является разложение детерминанта по Лапласу (Теорема Лапласа), дающее возможность вычислять определитель по любым k строкам (столбцам):

Определение через перестановки

Для матрицы справедлива формула:

,

где α₁,α₂,...,α_n — перестановка чисел от 1 до n, N(α₁,α₂,...,α_n) — число инверсий в перестановке, суммирование идёт по всем возможным перестановкам порядка n. Таким образом, в определитель войдёт n! слагаемых, которые также называют «членами определителя». Важно заметить, что во многих курсах линейной алгебры это определение даётся как основное.

3)Обратные матрицы Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

Свойства обратной матрицы

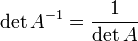• , где 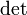обозначает определитель.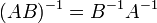

• для любых двух обратимых матриц A и B.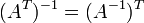

• где * ^T обозначает транспонированную матрицу.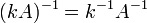

• для любого коэффициента .

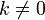• Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если A ^{− 1} существует, то x = A ^{− 1}b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.

Способы нахождения обратной матрицы

Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:

Точные (прямые) методы Метод Гаусса—Жордана

Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A⁻¹.

При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц Λ_i (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):

.

.

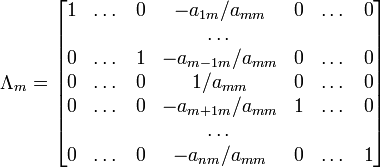Вторая матрица после применения всех операций станет равна Λ, то есть будет искомой. Сложность алгоритма — O(n³).

С помощью матрицы алгебраических дополнений

C^T — транспонированная матрица алгебраических дополнений;

Полученная матрица A⁻¹ и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя O_det и равна O(n²)·O_det.

Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополнений элементов исходной матрицы.

[.] Использование lu/lup-разложения

Матричное уравнение AX = I_n для обратной матрицы X можно рассматривать как совокупность n систем вида Ax = b. Обозначим i-ый столбец матрицы X через X_i; тогда AX_i = e_i, ,поскольку i-м столбцом матрицы I_n является единичный вектор e_i. другими словами, нахождение обратной матрицы сводится к решению n уравнений с одной матрицей и разными правыми частями. После выполнения LUP-разложения (время O(n³)) на решение каждого из n уравнений нужно время O(n²), так что и эта часть работы требует времени O(n³)^[1].

Если матрица A невырождена, то для неё можно рассчитать LUP-разложение PA = LU. Пусть PA = B, B ^{− 1} = D. Тогда из свойств обратной матрицы можно записать: D = U ^{− 1}L ^{− 1}. Если умножить это равенство на U и L то можно получить два равенства вида UD = L ^{− 1} и DL = U ^{− 1}. Первое из этих равенств представляет собой систему из n² линейных уравнений для из которых известны правые части (из свойств треугольных матриц). Второе представляет также систему из n² линейных уравнений для из которых известны правые части (также из свойств треугольных матриц). Вместе они представляют собой систему из n² равенств. С помощью этих равенств можно реккурентно определить все n² элементов матрицы D. Тогда из равенства (PA)⁻¹ = A⁻¹P⁻¹ = B⁻¹ = D. получаем равенство A ^{− 1} = DP.

В случае использования LU-разложения не требуется перестановки столбцов матрицы D но решение может разойтись даже если матрица A невырождена.

Сложность алгоритма — O(n³).

Итерационные методы

Методы Шульца

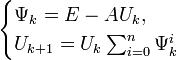
Оценка погрешности

Выбор начального приближения

Проблема выбора начального приближения в рассматриваемых здесь процессах итерационного обращения матриц не позволяет относиться к ним как к самостоятельным универсальным методам, конкурирующими с прямыми методами обращения, основанными, например, на LU-разложении матриц. Имеются некоторые рекомендации по выбору , обеспечивающие выполнение условия (спектральный радиус матрицы меньше единицы), являющегося необходимым и достаточным для сходимости процесса. Однако при этом, во-первых, требуется знать сверху оценку спектра обращаемой матрицы A либо матрицы (а именно, если A — симметричная положительно определённая матрица и , то можно взять , где 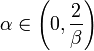; если же A — произвольная невырожденная матрица и , то полагают , где также ; можно конечно упростить ситуацию и, воспользовавшись тем, что , положить ). Во-вторых, при таком задании начальной матрицы нет гарантии, что будет малой (возможно, даже окажется ), и высокий порядок скорости сходимости обнаружится далеко не сразу. Примеры

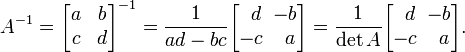
Обращение матрицы 2х2 возможно только при условии, что .