
- •Теория механизмов и машин
- •Предисловие
- •Введение
- •Узкое определение машины. Машина есть устройство, действующее на основе законов механики и предназначенное для преобразования энергии, материалов и информации и перемещения изделий.
- •Раздел 1. Структура, кинематика
- •1. Структура механизмов
- •1.1. Классификация кинематических пар
- •1.2. Кинематические цепи и их классификация
- •1.3. Расчет степени подвижности механизма
- •1.4. Структурная классификация плоских механизмов
- •1.5. Замена высших пар в плоских механизмах
- •1.6. Избыточные (повторяющиеся) связи и местные подвижности в механизмах
- •1.7. Структурный синтез механизмов
- •Вопросы для самопроверки
- •2. Кинематика и синтез зубчатых механизмов
- •2.1. Разновидности зубчатых передач
- •2.2. Понятие о передаточном отношении
- •2.3. Передаточное отношение простых зубчатых передач
- •2.4. Кинематика и синтез зубчатых механизмов с неподвижными осями колес
- •2.5. Кинематика механизмов планетарного типа
- •2.6. Синтез механизмов планетарного типа
- •Вопросы для самопроверки
- •3.2. Кинематические и передаточные функции механизмов
- •3.3. Аналитический метод
- •3.4. Метод планов положений, скоростей и ускорений
- •3.5. Метод кинематических диаграмм (метод графического дифференцирования)
- •3.6. Синтез рычажных механизмов
- •Вопросы для самопроверки
- •Раздел 2. Кинетостатика
- •4. Кинетостатика механизмов
- •4.1. Характеристика сил, действующих в машинах
- •4.2. Задачи кинетостатики
- •4.3. Расчёт сил инерции
- •4.4. Общие положения силового расчёта
- •4.5. Метод планов сил
- •4.6. Метод разложения сил
- •4.7. Аналитический метод
- •4.8. Определение уравновешивающей силы
- •Вопросы для самопроверки
- •5. Трение в кинематических парах и кпд
- •5.1. Виды трения. Законы трения скольжения
- •5.2. Понятие о коэффициенте полезного действия
- •5.3. Трение в поступательной кинематической паре
- •5.4. Трение в винтовой кинематической паре
- •5.5. Трение во вращательной кинематической паре
- •5.6. Трение качения
- •Вопросы для самопроверки
- •6. Динамика машин
- •6.1. Вспомогательные задачи динамики машин
- •6.2. Характеристики режимов движения машин
- •I . Неустановившийся режим
- •II. Установившийся режим
- •6.3. Формы уравнений движения машин
- •6.4. Исследование пуска машины при силах – функциях перемещений
- •6.5. Исследование установившегося неравновесного движения машины с маховиком при силах – функциях перемещений
- •6.6. Определение момента инерции маховика при внешних силах – функциях перемещений
- •6.7. Назначение маховика в машине
- •6.8. Исследование пуска машины при силах – функциях скоростей
- •6.9. Исследование устойчивости установившегося равновесного движения
- •Вопросы для самопроверки
- •7. Проблемы уравновешивания и балансировки звеньев и механизмов
- •7.1. Значение проблемы уравновешивания и балансировки в машинах
- •7.2. Виды неуравновешенности вращающихся звеньев и их устранение
- •7.3. Начальные сведения об уравновешивании механизмов
- •7.4. Виброгашение и виброизоляция
- •Вопросы для самопроверки
- •Раздел 3. Синтез элементов высших
- •8. Теория и геометрия зубчатых зацеплений
- •8.1. Элементы относительного движения звеньев высшей пары
- •8.2. Элементы зубчатых зацеплений, обусловленные их кинематикой
- •8.3. Основные качественные характеристики зацеплений
- •8.4. Эвольвента зуба колеса, её свойства и уравнение
- •8.5. Элементы зубчатого колеса
- •8.6. Элементы и свойства эвольвентного зацепления
- •8.7. Методы изготовления зубчатых колёс
- •8.8. Геометрия реечного производящего исходного контура
- •8.9. Подрез зуба колеса и его предотвращение
- •8.10. Качественные характеристики эвольвентного зацепления
- •8.11. Назначение коэффициентов смещения для нарезания зубчатых колёс
- •8.12. Типы эвольвентных колёс и передач
- •8.13. Расчёт геометрических размеров зубчатых колёс
- •8.14. Особенности зацепления эвольвентных косозубых колёс
- •8.15. Особенности зацепления конических колёс
- •8.16. Особенности зацепления в гиперболоидных передачах
- •Вопросы для самопроверки
- •9. Синтез профилей кулачков и элементов плоских кулачковых механизмов
- •9.1. Элементы кулачкового механизма и геометрические элементы кулачка
- •9.2. Разновидности плоских кулачковых механизмов
- •9.3. Кинематический анализ кулачковых механизмов
- •9.4. Понятие об ударах в кулачковых механизмах
- •9.5. Угол давления и его влияние на работоспособность кулачкового механизма
- •9.6. Связь между углом давления и геометро-кинематическими характеристиками механизма
- •9.7. Графическое определение угла давления
- •9.8. Определение радиуса основной окружности теоретического профиля кулачка
- •9.9. Определение радиуса основной окружности в механизме с плоским толкателем
- •9.10. Построение профилей вращающихся кулачков
- •Вопросы для самопроверки
- •Библиографический список
- •Оглавление
- •Раздел 1. Структура, кинематика и элементы синтеза механизмов
- •3. Кинематика и синтез механизмов с низшими кинематическими
- •Раздел 2. Кинетостатика механизмов и динамика машин
- •Раздел 3. Синтез элементов высших кинематических пар
- •9. Синтез профилей кулачков и элементов плоских кулачковых
8.5. Элементы зубчатого колеса
Здесь рассматриваются те элементы колеса, которые относятся к его ободу, где располагаются зубья (рис. 8.12).
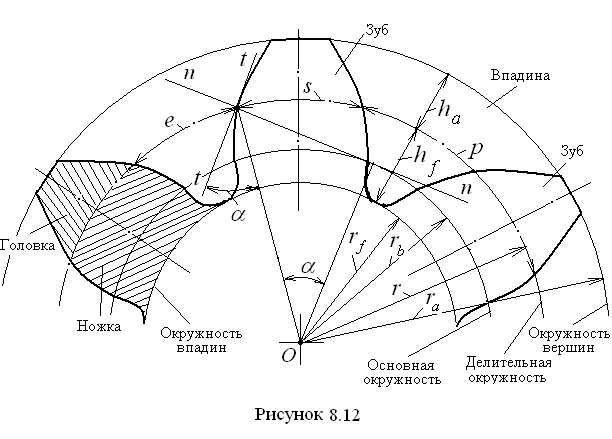 –
–
Шаг
колеса
– это
расстояние по делительной окружности
между одноимёнными профилями двух
соседних зубьев,
![]() .
Шаг включает два параметра – толщину
зуба
.
Шаг включает два параметра – толщину
зуба
![]() и
ширину впадины
и
ширину впадины
![]() .
Если
.
Если
![]() ,
то имеем колесо с равноделённым шагом,
в противном случае имеем колесо с
неравноделённым шагом.
,
то имеем колесо с равноделённым шагом,
в противном случае имеем колесо с
неравноделённым шагом.
Делительная окружность (её радиус ; в зацеплении двух колёс имеет индекс номера колеса):
– делит зуб на головку и ножку;
– модуль m на этой окружности имеет стандартное значение;
– радиус
окружности имеет величину
![]() ;
;
– в
точке на делительной окружности
профильный угол эвольвенты
![]() и обозначается буквой
без
индекса.
и обозначается буквой
без
индекса.
Основная
окружность
является базовой для образования
эвольвенты (от неё начинается эвольвентная
часть зуба). Радиус этой окружности
получается из рассмотрения прямоугольного
треугольника с углом при вершине O,
равным
,
и одним из катетов, равным
b,
и гипотенузой, равной
:
![]() .
.
Окружность вершин является габаритной окружностью колеса, её радиус определяется формулой
![]() ,
,
где
![]() –
высота головки зуба, причём
–
высота головки зуба, причём
![]() .
Множитель перед модулем называется
коэффициентом
высоты головки зуба
и равен по величине 1, то есть
.
Множитель перед модулем называется
коэффициентом
высоты головки зуба
и равен по величине 1, то есть
![]() .
.
Диаметр окружности вершин является диаметром заготовки для изготовления зубчатого колеса.
Окружность
впадин
ограничивает
зуб у основания. Её радиус определяется
разностью
![]() ,
где
,
где
![]() – высота ножки зуба, определяемая
равенством
– высота ножки зуба, определяемая
равенством
![]() ,
число
,
число
![]() в скобках называется коэффициентом
радиального зазора
и имеет величину
в скобках называется коэффициентом
радиального зазора
и имеет величину
![]() .
.
Полная
высота зуба, включающая головку и ножку,
составляет
![]() .
.
Контур зуба от основной окружности до окружности вершин очерчен эвольвентой, которая сопрягается с окружностью впадин переходной кривой (для сведения: эквидистантой удлинённой эвольвенты).
8.6. Элементы и свойства эвольвентного зацепления
Э л е м е н т ы з а ц е п л е н и я п а р ы к о л ё с. Отметим прежде всего, что здесь рассматриваются те элементы, которые имеются именно в зацеплении колёс, а у отдельного колеса их нет (рис. 8.13). К этим элементам относятся следующие.
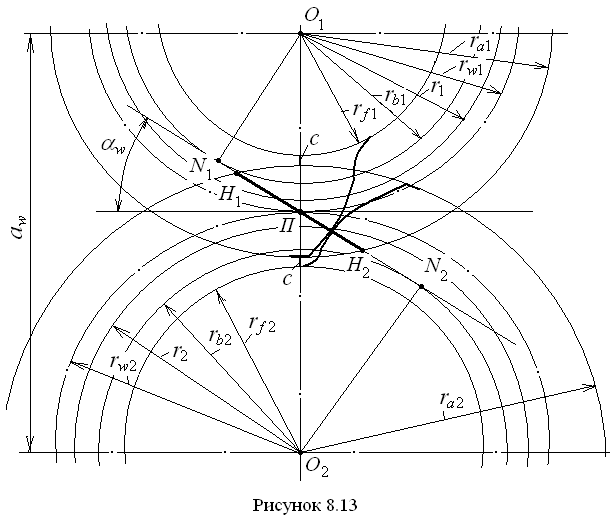
Межосевое
расстояние
– это расстояние между центрами колёс
O1
и O2.
Полюс
зацепления
П
–
это точка касания центроидных окружностей
колёс с радиусами
![]() и
и
![]() ,
которые в эвольвентном зацеплении
называются начальными
окружностями.
Теоретическая
линия зацепления
N1N2
– это
геометрическое место точек
мгновенного
касания профилей зубьев, отмеченное на
неподвижной плоскости.
Процесс передачи движения происходит
таким образом, что профили одной пары
зубьев на протяжении некоторого времени
касаются друг друга, то есть имеют общую
нормаль.
На основании первого свойства эвольвенты
нормаль к ней является касательной к
основной окружности, а для двух касающихся
друг друга профилей является касательной
к обеим основным окружностям. Поэтому
для данных профилей контактная нормаль
является единственной и лежит на общей
касательной к основным окружностям,
образуя, таким образом, прямолинейную
линию зацепления.
С учётом геометрических размеров
конкретных колёс линия зацепления
используется для передачи движения
только в пределах зоны, заключённой
между точками её пересечения с
окружностями вершин (рис. 8.13). Эта зона
называется активной
линией зацепления.
Её границы на рисунке отмечены точками
H1
и H2,
и она проведена жирной линией.
,
которые в эвольвентном зацеплении
называются начальными
окружностями.
Теоретическая
линия зацепления
N1N2
– это
геометрическое место точек
мгновенного
касания профилей зубьев, отмеченное на
неподвижной плоскости.
Процесс передачи движения происходит
таким образом, что профили одной пары
зубьев на протяжении некоторого времени
касаются друг друга, то есть имеют общую
нормаль.
На основании первого свойства эвольвенты
нормаль к ней является касательной к
основной окружности, а для двух касающихся
друг друга профилей является касательной
к обеим основным окружностям. Поэтому
для данных профилей контактная нормаль
является единственной и лежит на общей
касательной к основным окружностям,
образуя, таким образом, прямолинейную
линию зацепления.
С учётом геометрических размеров
конкретных колёс линия зацепления
используется для передачи движения
только в пределах зоны, заключённой
между точками её пересечения с
окружностями вершин (рис. 8.13). Эта зона
называется активной
линией зацепления.
Её границы на рисунке отмечены точками
H1
и H2,
и она проведена жирной линией.
Угол
зацепления
![]() – это угол
между линией зацепления и общей
касательной к начальным окружностям,
проведённой через полюс зацепления П.
– это угол
между линией зацепления и общей
касательной к начальным окружностям,
проведённой через полюс зацепления П.
Сопряжённые (или парные) точки – это точки профилей зубьев, которыми они касаются друг друга на линии зацепления.
Радиальный
зазор
– это расстояние c
на межосевой линии между точками
пересечения её с окружностью вершин
одного колеса и впадин другого колеса.
Величина радиального зазора равна
![]() ,
где
– это коэффициент радиального зазора,
в соответствии со стандартом равный
0,25.
,
где
– это коэффициент радиального зазора,
в соответствии со стандартом равный
0,25.
С в о й с т в а э в о л ь в е н т н о г о з а ц е п л е н и я.
1.
Передаточное
отношение
постоянно
в любой фазе зацепления, так как
оно
может
быть выражено
через
радиусы основных окружностей.
Для доказательства используем подобные
прямоугольные треугольники (рис. 8.13)
![]() и
и
![]() и запишем цепочку равенств:
и запишем цепочку равенств:
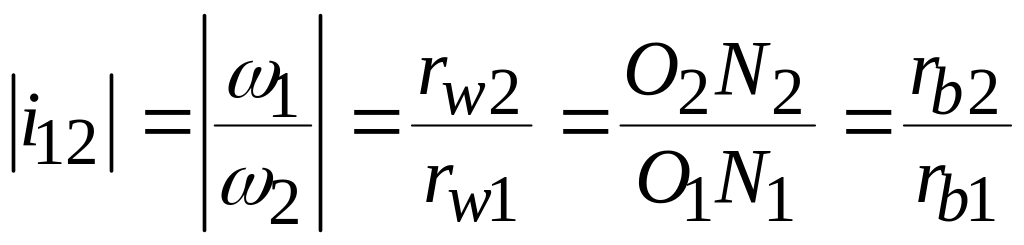 .
.
2. Передаточное отношение не зависит от изменения межосевого расстояния по той же причине, что и в предыдущем случае. Для компенсации погрешностей углового положения осей колёс применяют бочкообразные зубья.
3. Правильное зацепление эвольвентных профилей происходит только в пределах линии зацепления N1N2, так как только в этих пределах контактирующие эвольвентные профили имеют общую нормаль.
4. Эвольвентные колёса одного модуля имеют полную взаимозаменяемость, то есть могут составить правильное зацепление.
