5.4. Трение в винтовой кинематической паре

Р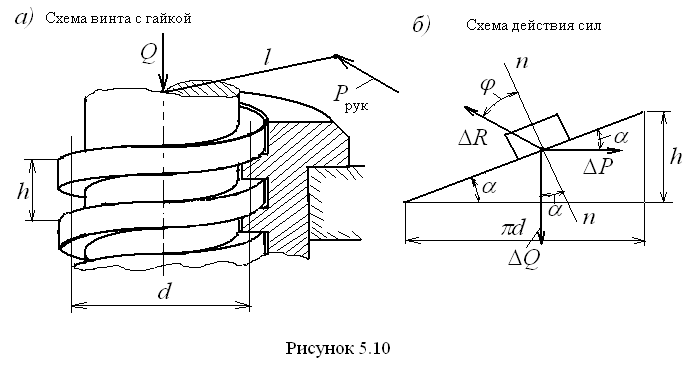 ассмотрим винтовую кинематическую пару с прямоугольной или трапецоидальной резьбой (рис. 5.10, а). Вдоль оси винта действует сила Q вертикально вниз, прижимая витки винта к виткам гайки. Средний диаметр винта обозначен d, шаг – h. Шагом винта называется расстояние между одноимёнными точками двух соседних выступов, измеренное в осевом направлении, нельзя путать шаг с ходом винта, который представляет собой осевое перемещение винта за один его оборот. Если имеется так называемый однозаходный винт, то шаг и ход совпадают, при n-заходном винте ход равен (n = 1, 2, 3, …) Далее рассматривается однозаходный винт.

Развернём среднюю винтовую линию на плоскость (рис. 5.10, б), в результате чего получим прямоугольный треугольник, горизонтальный катет которого равен , а вертикальный – шагу h. При этом винтовая линия превратится в наклонную плоскость, рассмотренную ранее. Возьмём небольшой участок витка винта на этой наклонной плоскости и покажем действующие на него силы. Так как рассматривается не весь виток, а только его небольшая часть, то силы, приходящиеся на него, составляют только части полных сил, то есть , и . При этом движущей силой является , действующая горизонтально. Сила действует вертикально вниз, а отклонена от нормали n-n к наклонной плоскости на угол .

По существу, на схеме рис. 5.10, б имеем частный случай 2 из рассмотренного выше движения ползуна по наклонной плоскости. Для этого случая сила определяется формулой . Суммируя по всей длине витка на протяжении одного оборота, получаем полную силу на окружности диаметра d: . Момент этой силы относительно оси винта равен произведению её на средний радиус, то есть . И, наконец, усилие на рукоятке для вращения винта составляет величину, равную отношению момента M к длине рукоятки l: .

Самотормозящийся винт получается, если, как и в случае наклонной плоскости, угол подъёма винтовой линии меньше угла трения . Самотормозящийся винт не будет вращаться при любой осевой силе Q. Легко себе представить, что с увеличением количества заходов угол увеличивается, и можно получить несамотормозящийся винт, который станет вращаться под действием осевой нагрузки.

Для вычисления КПД винтовой пары необходимо найти работу полезной силы Q по подъёму винта за один его оборот, то есть на величину h, и работу движущего момента M за один оборот, то есть на угол . Первая из них равна , вторая – , поэтому

.

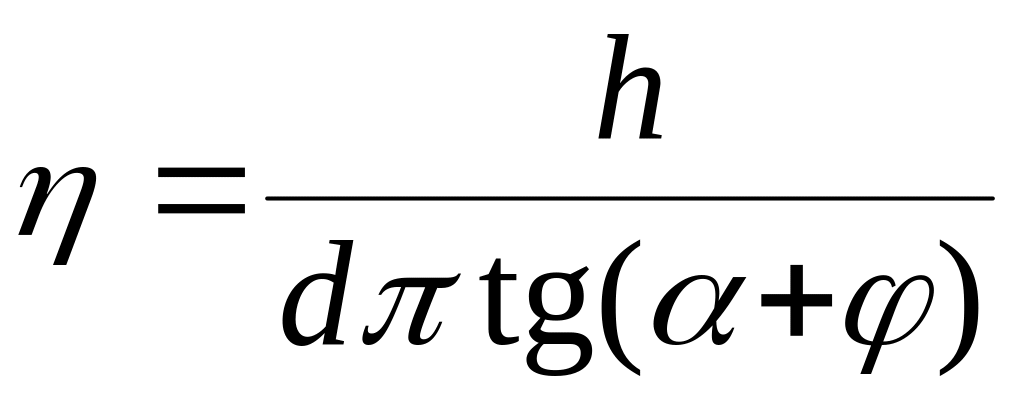Из рис. 5.10, б видно, что отношение , поэтому окончательно имеем

.

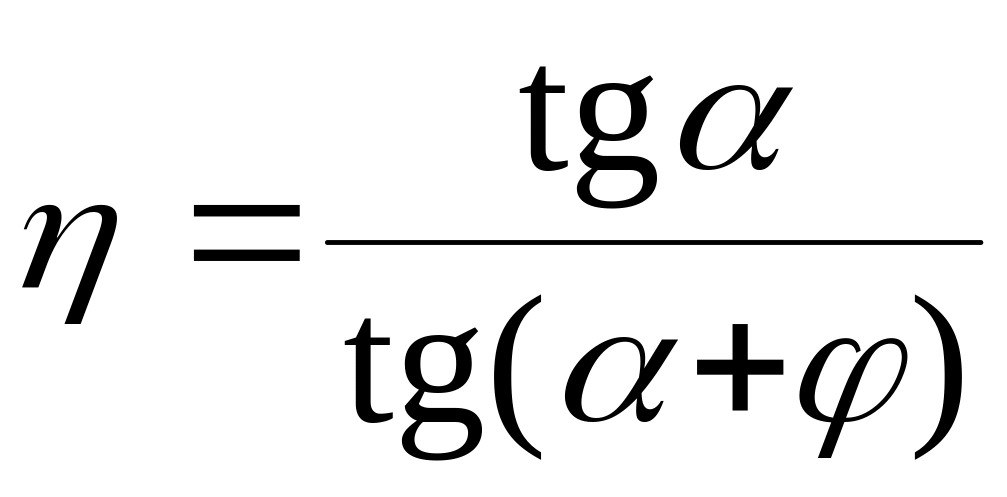5.5. Трение во вращательной кинематической паре

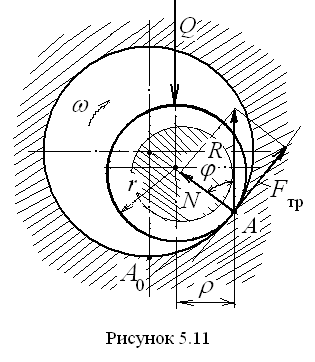
Рассмотрим вращательную кинематическую пару в наиболее часто встречающемся случае, когда сопряжение вала с отверстием осуществляется с зазором (рис. 5.11). На указанном рисунке зазор между валом и отверстием весьма преувеличен для того, чтобы лучше видеть элементы сопряжения. Вал нагружен поперечной силой , которая является известной величиной. При отсутствии вращения окружность вала касается окружности отверстия в точке на его вертикальном диаметре. Когда вал вращается в направлении , то, в результате действия силы трения , он «взбирается» на стенку вала и в равновесном состоянии устанавливается, касаясь окружности отверстия в точке . При этом реакция стенки отверстия равна и противоположна силе . Нормальная реакция направлена вдоль нормали в точке касания окружностей, то есть вдоль линии, проходящей через точку касания и их центры. Сила трения направлена по касательной к окружностям, проходящей также через точку касания , навстречу окружной скорости вала. Радиус цапфы вала обозначен r (цапфой называется участок вала, который находится внутри отверстия опоры).

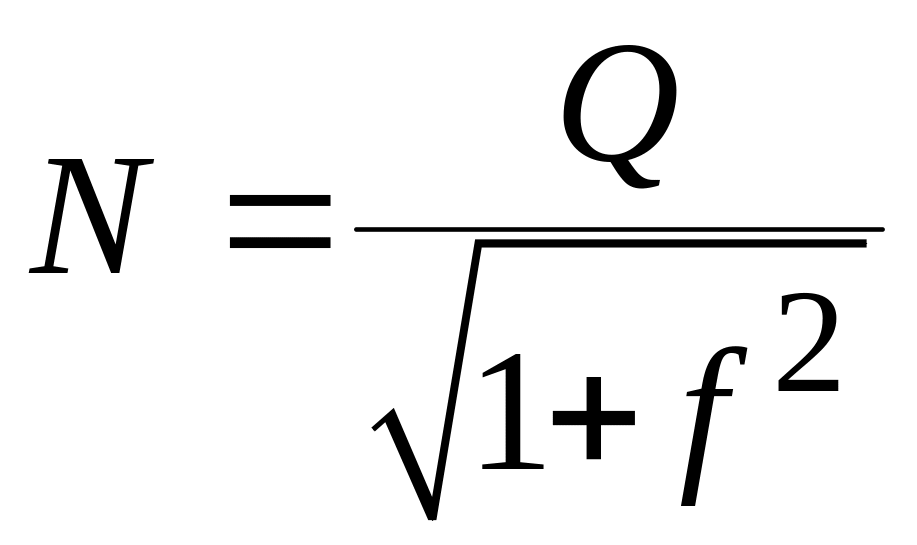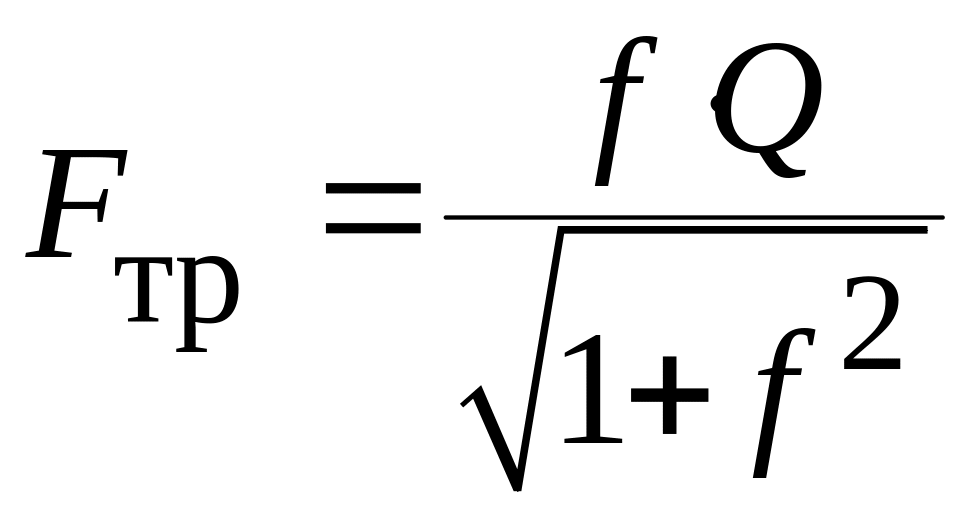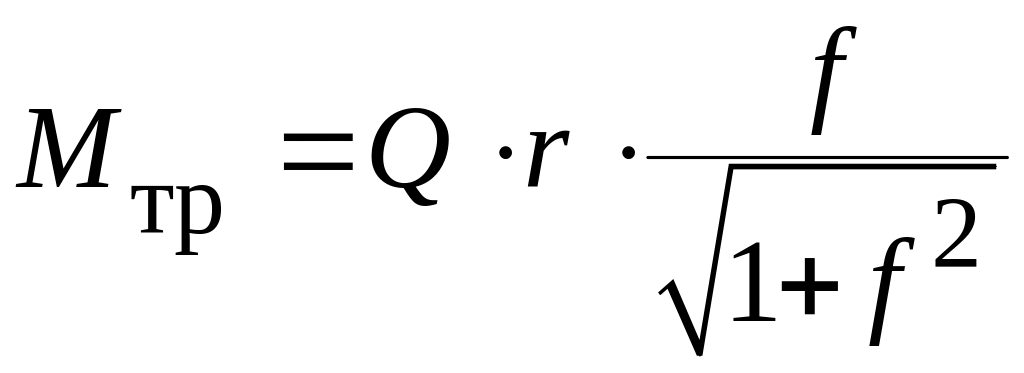Сопротивление вращению вала создаётся моментом трения , равным произведению силы трения на радиус цапфы, то есть . Сила трения, как известно, определяется формулой . Из силового треугольника по теореме Пифагора имеем , или , откуда . Поэтому сила трения , а момент трения . Так как коэффициент трения , то , тогда (например, , , а ). Поэтому можно принять, что . Произведение радиуса цапфы на коэффициент трения является для данных условий постоянной величиной, определяемой только геометрией вала и условиями трения. Эта величина измеряется в линейных единицах, обозначается и называется кругом трения, который описывается этим радиусом при вращении вала (круг трения на рис. 5.11 заштрихован). Так что радиус круга трения . Таким образом, при известном момент трения вычисляется по формуле .

Значение круга трения заключается в том, что полная реакция во вращательной паре проходит по касательной к нему, никогда не пересекая его. При этом её направление таково, что момент реакции относительно центра вала направлен против скорости вращения вала.

Р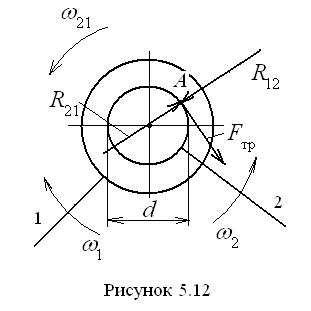 а с ч ё т п о т е р ь м о щ н о с т и н а т р е н и е в о в р а щ а т е л ь -н о й п а р е. Реакции в кинематических парах, вычисляемые с помощью методов планов сил и других методов, являются, по существу, нормальными реакциями, так как они определялись в предположении отсутствия трения. Это значит, что коэффициент трения предполагался равным нулю, и, соответственно угол трения также принимался равным нулю. Поэтому для определения мощности трения необходимо знать момент силы трения и относительную угловую скорость одного звена пары по отношению к другому, то есть . Представим на рис. 5.12 вращательную пару, образованную звеньями 1 и 2, с увеличенным изображением её элементов. Предположим, что касание элементов пары происходит в точке A. В этой точке действуют реакции со стороны первого звена на второе и со стороны второго звена на первое. В этой же точке приложена сила трения , препятствующая движению второго звена относительно первого. Сила трения определяется формулой (здесь и далее имеется в виду, что рассматривается движение второго звена относительно первого, а не наоборот). Из рисунка видно, что момент трения может быть определён как , где d – диаметр цапфы вала. Относительная угловая скорость определяется с помощью метода обращения движения: если обоим звеньям пары сообщить движение с угловой скоростью, равной и противоположно направленной угловой скорости звена 1, то это звено остановится, а второе будет вокруг него вращаться с угловой скоростью , которая и будет относительной скоростью звена 2 относительно звена 1. Таким образом, мощность трения, равная , окончательно выразится формулой

.