3.3. Аналитический метод

Метод заключается в определении математических выражений, описы-вающих функциональную связь между входными и выходными параметрами механизма. Для этого служат различные приёмы и методы, такие как метод векторных контуров, который образуется заменой кинематических размеров звеньев векторами, с последующим проецированием этого контура на оси системы координат и получением на этой основе соответствующих уравнений, описывающих кинематику данного механизма. Этой же цели служит метод разбиения схемы механизма на прямо- или косоугольные треугольники, решая которые, получают необходимые математические выражения. Для составления некоторого первоначального представления о методе рассмотрим кинематику двух несложных механизмов.

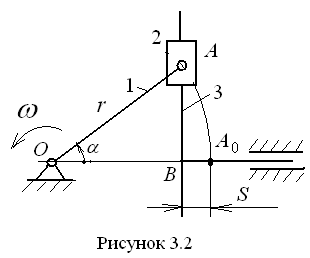
С и н у с н ы й м е х а н и з м (рис. 3.2) состоит из кривошипа, вращающегося вокруг неподвижной точки О, конец А которого образует вращательную кинематическую пару с ползуном 2. Ползун движется по вертикальному элементу ведомого звена 3, которое движется вдоль неподвижных горизонтальных направляющих. На первом этапе определяется зависимость перемещения S ведомого звена от угла α поворота ведущего кривошипа 1. Из рис. 3.2 видно, что

.

Дифференцируя по в первый раз, получаем аналог скорости ведомого звена

,

дифференцируя во второй раз, получаем аналог ускорения ведомого звена

.

Для расчёта скорости и ускорения ведомого звена необходимо воспользоваться выражениями

К р и в о ш и п н о-п о л з у н н ы й м е х а н и з м (рис. 3.3) широко известен тем, что применяется во многих областях техники, например в качестве основного механизма двигателей внутреннего сгорания, поршневых насосов, компрессоров, в полиграфической технике – в станках для обработки стереотипов и др.

Схему механизма возьмём в наиболее общем виде, когда направляющая точки B не проходит через центр вращения кривошипа O₁, а располагается от неё на расстоянии e, называемом эксцентриситетом. В данной схеме эксцентриситет принимается отрицательным, так как отложен вниз от точки O₁. Если он отложен вверх, то считается положительным. В связи с наличием e механизм называется эксцентричным или нецентральным. Он состоит из кривошипа 1, вращающегося относительно стойки 0 вокруг точки O₁ с угловой скоростью ω₁, так что точка A описывает окружность радиусом r. От кривошипа движение передаётся с помощью шатуна 2 длиной l на ползун 3, который движется возвратно-поступательно вдоль горизонтальных направляющих. В крайнем правом положении точка B ползуна занимает положение B₀. При этом кривошип 1 и шатун 2 выстраиваются в одну прямую O₁B₀, образующую угол ν (ню) с горизонталью, синус которого определяется формулой , и точка A занимает положение A₀ на линии O₁B₀. В текущем положении кривошип 1 повернут относительно его крайнего положения на угол α в сторону вращения. При этом точка B переместилась от её крайнего положения на величину S.

З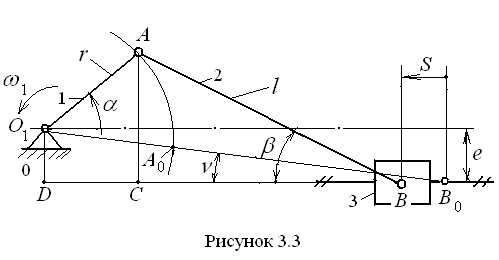 адача исследования кинематики механизма состоит в определении функции положения и её первой и второй производных, то есть аналогов скоростей и ускорений.

Как видно из рис. 3.3, перемещение точки B от крайнего положения B₀ можно выразить как S=DB₀ – DB, причём, DB₀ , согласно теореме Пифагора, определяется как , а .

Для определения угла выразим длину вертикального отрезка двумя путями, получая двойное равенство: имеем , от-куда , или , где , является одной из геометрических характеристик механизма и находится обычно в пределах , а . Имея в виду соотношение между синусом и косинусом, получаем . Подставляя в S все най-

денные выражения, получаем

.

Или

.

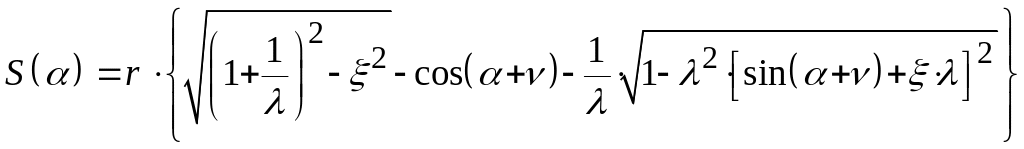Для перехода к аналогам скорости и ускорения необходимо это выражение продифференцировать дважды по , то есть получить выражения вида

и .

С привлечением для вычислительного процесса такого математического пакета, как MathCAD, нет необходимости выводить расчётные зависимости и , так как сама программа по соответствующей команде выведет необходимые выражения и выполнит по ним расчёт.

Пример. Рассмотрим составление программы и решение по ней задачи исследования кинематики кривошипно-ползунного механизма в математическом пакете MathCAD 2001i Professional (Листинг 3.1)

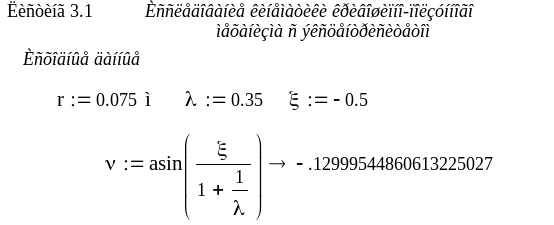
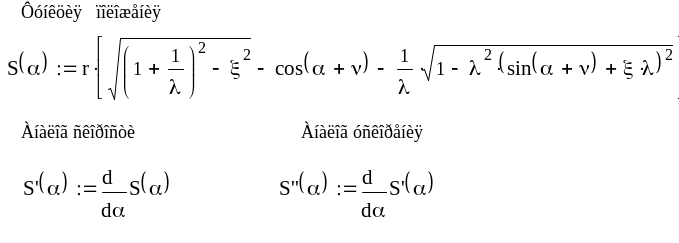
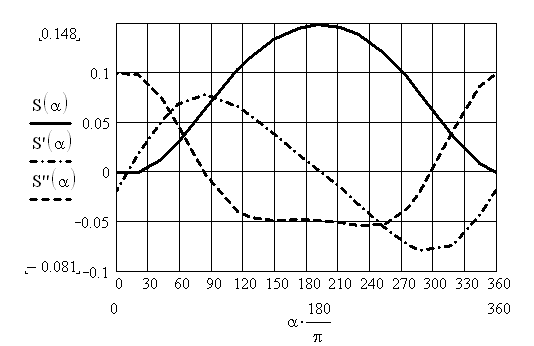
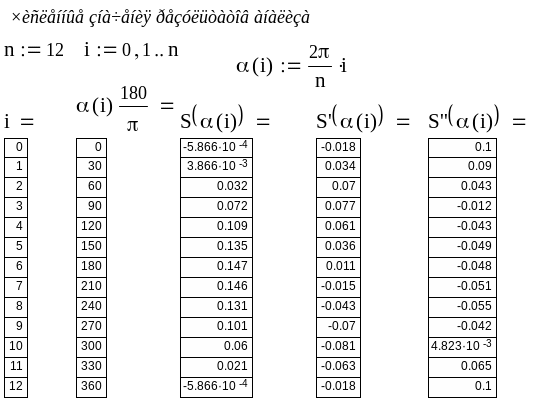
Так как угол удобнее брать в градусах, а программа MathCAD требует применения угла в радианной мере, то на графиках ось абсцисс обозначена формулой перевода угла α из радианной меры в градусную.

Для получения численных результатов анализа необходимо ввести ранжированную переменную , которой нужно задать пределы изменения от 0 до и шаг. Необходимо также ввести эту переменную как аргумент для изменения , то есть представить как функцию в виде .

Для расчёта скоростей и ускорений точки B ползуна достаточно воспользоваться следующими формулами перехода

и .

При этом те же графики, но с другими масштабами по осям ординат будут графиками изменения указанных кинематических функций. Численные значения кинематических функций можно получить также с помощью введения ранжированной переменной.