47. Статистические игры. Критерии для принятия решений
зависят не от сознательных действий другого игрока, а от объективной действительности, которую принято называть «природой». Такие игры называются играми с природой.
В некоторых задачах для состояний природы может быть задано распределение вероятностей, в других — оно неизвестно. Условия игры задаются матрицей
А=(aij)=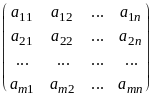
.
Элемент aij равен выигрышу игрока А, если он использует стратегию Аi, а состояние природы — Pj. В ряде случаев рассматривают матрицу риска R. Элементы матрицы риска rij представляют собой разность между выигрышем, который получил бы игрок А, если бы знал состояние Pj, и выигрышем, который он получит в тех же условиях, применяя стратегию Аi, т. е.
rij=j- aij, где j= .
Критерий Байеса.
Если вероятности
состояния природы Pj
равны qj
(j=1...n),
=1,
то выбор i-стратегии
обеспечивает математическое ожидание
выигрыша, равное
. Принимается решение об использовании
стратегии, для которой имеет место
.
Максиминный критерий Вальда. Этот критерий совпадает с критерием выбора стратегии, позволяющим получить нижнюю цену игры для двух лиц с нулевой суммой. Согласно этому критерию выбирается стратегия, гарантирующая при любых условиях выигрыши, не меньше, чем
.
Критерий минимального риска Сэвиджа. Этот критерий рекомендует выбирать в качестве оптимальной ту стратегию, при которой величина риска минимизируется в наихудших условиях, т. е. обеспечивается
.
Критерии Вальда и Сэвиджа основаны на самой пессимистической оценке обстановки.
Критерий Гурвица является критерием пессимизма-оптимизма. За оптимальную принимается та стратегия, для которой выполняется соотношение
,
где
.
При =0 имеем критерий крайнего оптимизма, а при =1 — критерий пессимизма Вальда. При желании подстраховаться в данной ситуации принимают близким к единице.
48.Общая постановка задачи нелинейного программирования
Если в задаче математического программирования целевая функция z ( x ) и (или) хотя бы одна из функций системы ограничений i ( x ) нелинейна, то такой раздел называется нелинейным программированием (НЛП).
В общем виде задача нелинейного программирования (ЗНЛП) состоит в определении максимального (минимального) значения функции
z=f (x1, x2, ... xn) (3.1)
при условии, что ее переменные удовлетворяют соотношениям
gi (x1, x2, ..., xn)=bi, i=1, 2, ..., k, (3.2)
gi (x1, x2, ..., xn)<=bi, i=k+1, k+2, ..., m.
Если f и g — линейные функции, то задача (3.1), (3.2) является задачей линейного программирования.
Соотношения (3.2) образуют систему ограничений и включают в себя условия не отрицательности переменных, если такие условия имеются. Условия не отрицательности могут быть заданы и непосредственно.
49. Геометрическая интерпретация задачи нелинейного программирования
50. Геометрический способ решения задачи нелинейного программирования
В евклидовом пространстве Еn система ограничений gi (x1, x2, ..., xn)=bi, i=1, 2, ..., k, определяет область допустимых решений задачи (ОДР). В отличие от ЗЛП она не всегда является выпуклой.
Если определена ОДР, то нахождение решения задачи сводится к определению такой точки этой области, через которую проходит гиперповерхность наивысшего (наинизшего) уровня: f (x1, x2, ..., xn)=h. Указанная точка может находиться как на границе ОДР, так и внутри нее.
Если в ЗЛП точки экстремума являются вершинами многогранников решений, то в задачах с нелинейной целевой функцией они могут лежать внутри области, на ребре (грани) или в вершине многогранника. Таким образом, с помощью методов линейного программирования, позволяющих осуществить переход из одной вершины многогранника в другую, можно получить оптимальное решение нелинейных задач при условии, что целевая функция удовлетворяет добавочным ограничениям.
Рассмотрение ЗНЛП начинают с классической задачи оптимизации. Задачи такого рода имеют место, если система (3.2) содержит только уравнения, отсутствуют условия не отрицательности и цело численности переменных, а функции gi (x1, x2, ..., xn) и f (x1, x2, ..., xn) непрерывны и имеют частные производные не ниже второго порядка. Классические методы оптимизации при этом являются теоретическим аппаратом, позволяющим в ряде случаев обосновать разработку соответствующего вычислительного метода.