
- •Постройте схему сети обратной связи, где каждый слой имеет по 3 нейрона
- •Matlab. Алгоритм реализации задачи аппроксимации
- •Matlab. Основные функции для работы с нейронными сетями
- •Matlab. Реализация задачи кластеризации, способы представления начальных данных.
- •Matlab. Функции для операций с матрицами Создание матриц с заданными свойствами Создание единичной матрицы
- •Cоздание матрицы с единичными элементами
- •Создание матрицы с нулевыми элементами
- •Конкатенация матриц
- •Элементов матриц
- •Вычисление произведений
- •Суммирование элементов
- •Функции формирования матриц
- •Поворот матриц
- •Выделение треугольных частей матриц
- •Матричные функции
- •Matlab. Многомерные массивы
- •Применение оператора «:» в многомерных массивах
- •Доступ к отдельному элементу многомерного массива
- •Работа с размерностями Вычисление числа размерностей массива
- •Вычисление размера размерности массива
- •Matlab. Функции для работы с графикой Построение графиков отрезками прямых
- •Графики в логарифмическом масштабе
- •Графики в полулогарифмическом масштабе
- •Столбцовые диаграммы
- •Вывод пояснений
- •Управление свойствами осей графиков
- •Включение и выключение сетки
- •Наложение графиков друг на друга
- •Разбиение графического окна
- •Изменение масштаба графика
- •Установка палитры цветов
- •Окраска плоских многоугольников
- •Вывод шкалы цветов
- •Цветные плоские круговые диаграммы
- •Matlab. Операции с файлами. Управляющие структуры
Нейрон получает входной сигнал от четырех других нейронов, уровни возбуждения которых равны
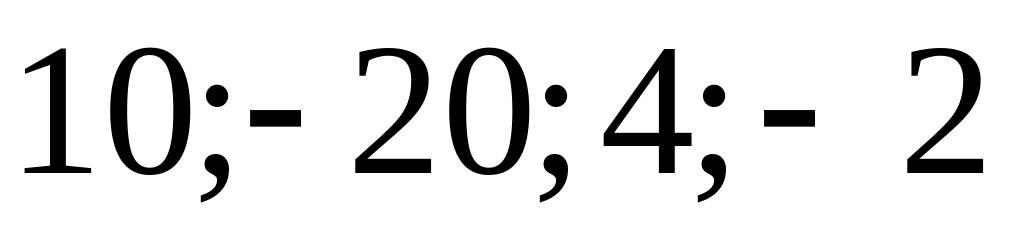 .
Соответствующие синаптические веса
равны
.
Соответствующие синаптические веса
равны
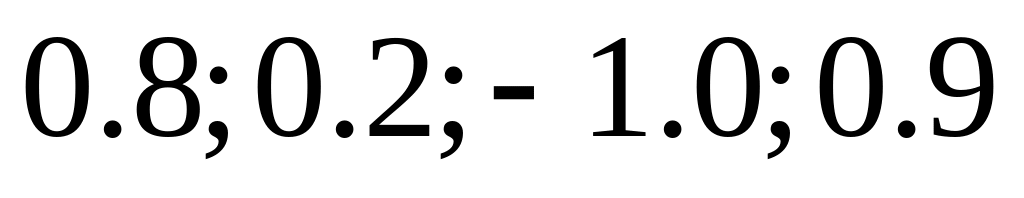 .
Вычислите выходной сигнал такого
нейрона, если нейрон представлен моделью
МакКаллока-Питтса.
.
Вычислите выходной сигнал такого
нейрона, если нейрон представлен моделью
МакКаллока-Питтса.
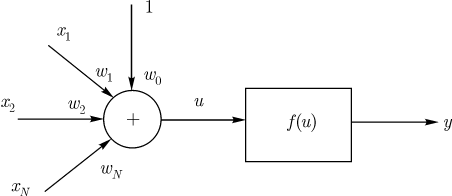
x1=10 x2=-20 x3=4 x5=-2
w1=0.8 w2=0.2 w3=-1 w4=0.9
net= u = x1w1 + x2w2 + x3w3 + x4w4 = 8 – 4 – 4 - 1.8 = -1.8
if net<0 then out=y=0
else out=y=1
=> out=0.
Нейрон получает входной сигнал от четырех других нейронов, уровни возбуждения которых равны . Соответствующие синаптические веса равны . Вычислите выходной сигнал такого нейрона, если нейрон имеет сигмоидальную функцию активации
x1=10 x2=-20 x3=4 x5=-2
w1=0.8 w2=0.2 w3=-1 w4=0.9
u=x1w1+x2w2+x3w3+x4w4=8-4-4-1.8=-1.8
y=out=1/(1-exp(-u))=1/(1-exp(1.8))
Постройте схему полносвязной сети прямого распространения, в которой входной и скрытый слои содержат по 3 нейрона, а выходной слой содержит 2 нейрона
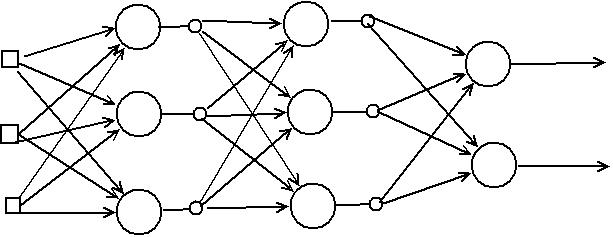
Постройте схему рекуррентной сети, состоящей из трех нейронов, не имеющих обратных связей с самими собой.
Нейрон получает входной сигнал от четырех других нейронов, уровни возбуждения которых равны . Соответствующие синаптические веса равны . Вычислите выходной сигнал такого нейрона, если нейрон имеет функцией активации гиперболический тангенс.
x1=10 x2=-20 x3=4 x5=-2
w1=0.8 w2=0.2 w3=-1 w4=0.9
u=x1w1+x2w2+x3w3+x4w4=8-4-4-1.8=-1.8
y=out= (1+exp(-u))/(1-exp(-u))= (1 + exp(1.8)/(1-exp(1.8))
Нейрон получает входной сигнал от четырех других нейронов, уровни возбуждения которых равны . Соответствующие синаптические веса равны . Вычислите выходной сигнал такого нейрона, если нейрон имеет функцией активации функцию Гаусса.
x1=10 x2=-20 x3=4 x5=-2
w1=0.8 w2=0.2 w3=-1 w4=0.9
u=x1w1+x2w2+x3w3+x4w4=8-4-4-1.8=-1.8
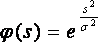
![]() ,
,
Постройте схему однослойной полносвязной сети прямого распространения, состоящей из 3 нейронов
Однослойный персептрон (персептрон Розенблатта) - однослойная нейронная сеть, все нейроны которой имеют жесткую пороговую функцию активации.
Однослойный персептрон имеет простой алгоритм обучения и способен решать лишь самые простые задачи. Эта модель вызвала к себе большой интерес в начале 1960-х годов и стала толчком к развитию искусственных нейронных сетей.
Классический пример такой нейронной сети - однослойный трехнейронный персептрон - представлен на рис. 11.3.
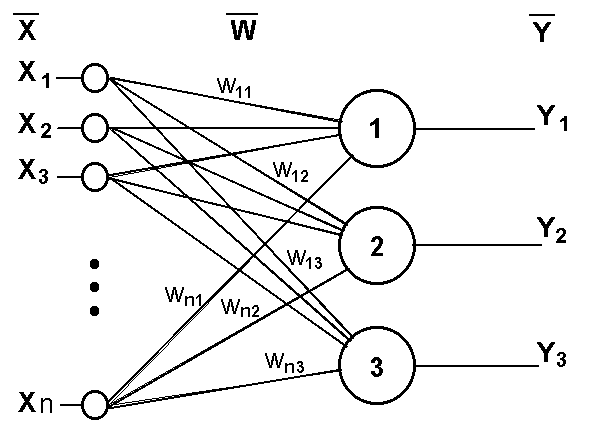
Рис. 11.3. Однослойный трехнейронный персептрон
Сеть, изображенная на рисунке, имеет n входов, на которые поступают сигналы, идущие по синапсам на 3 нейрона. Эти три нейрона образуют единственный слой данной сети и выдают три выходных сигнала.
Постройте схему сети обратной связи, где каждый слой имеет по 3 нейрона
Многослойные рекуррентные сети представляют собой развитие однонаправленных сетей персептронного типа за счет добавления в них соответствующих обратных связей. Обратная связь может исходить либо из выходного, либо из скрытого слоя нейронов. В каждом контуре такой связи присутствует элемент единичной задержки, благодаря которому поток сигналов может считаться однонаправленным (выходной сигнал предыдущего временного цикла рассматривается как априори заданный, который просто увеличивает размерность входного вектора сети). Представленная подобным образом рекуррентная сеть, с учетом способа формирования выходного сигнала, функционирует как однонаправленная персептронная сеть. Тем не менее, алгоритм обучения такой сети, адаптирующий значения синаптических весов, является более сложным из-за зависимости сигналов в момент времени от их значений в предыдущие моменты и соответственно из-за более громоздкой формулы для расчета вектора градиента.
При обсуждении рекуррентных сетей, в которых в качестве выходного элемента используется многослойный персептрон, рассмотрим наиболее известные структуры сетей RMLP, RTRN, Эльмана.
Персептронная сеть с обратной связью
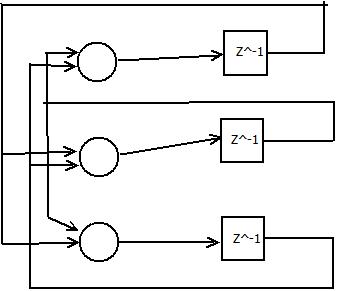
Один из простейших способов построения рекуррентной сети на базе однонаправленной HC состоит во введении в персептронную сеть обратной связи. В дальнейшем мы будем сокращенно называть такую сеть RMLP (англ.: Recurrent MultiLayer Perceptron - рекуррентный многослойный персептрон). Ее обобщенная структура представлена на рис. 1 ( - единичные элементы запаздывания).

Схема обучения нейронной сети, где каждый нейрона описан стохастической моделью.
Рассмотренная ранее модель нейрона является детерминированной. Это значит, что преобразование входного сигнала в выходной задается некоторой однозначной функцией, определенной на всем множестве входных сигналов. Однако, в некоторых приложениях применяется стохастическая модель нейрона, в которой функция активации носит вероятностный характер.
В таких моделях выходной сигнал нейрона может быть +1 и -1 и определяется с учетом вероятности каждого из исходов. Таким образом, функция активации для стохастического нейрона будет иметь вид:
![]() ,
(7.10)
,
(7.10)
где
![]() - это вероятность активации нейрона, а
- это вероятность активации нейрона, а
![]() это
индуцированное локальное поле нейрона
(сигнал, который формируется на выходе
сумматора).
это
индуцированное локальное поле нейрона
(сигнал, который формируется на выходе
сумматора).
Вероятность активации нейрона может быть описана сигмоидальной функцией следующего вида:
![]() ,
(7.11)
,
(7.11)
где
![]() - это аналог температуры, используемый
для управления степенью неопределенности
переключения. Следует отметить, что
величина
не описывает физическую температуру
нейронной сети.
- это аналог температуры, используемый
для управления степенью неопределенности
переключения. Следует отметить, что
величина
не описывает физическую температуру
нейронной сети.
Очевидно,
что при
![]() стохастический нейрон принимает
детерминированную форму нейрона со
ступенчатой функцией активации вида:
стохастический нейрон принимает
детерминированную форму нейрона со
ступенчатой функцией активации вида:
![]() (7.12)
(7.12)
Стохастические методы полезны как для обучения искусственных нейронных сетей, так и для получения выхода от уже обученной сети. Стохастические методы обучения приносят большую пользу, позволяя исключать локальные минимумы в процессе обучения. Но с ними также связан ряд проблем.
Использование обучения
Искусственная нейронная сеть обучается с помощью некоторого процесса, модифицирующего ее веса. Если обучение успешно, то предъявление сети множества входных сигналов приводит к появлению желаемого множества выходных сигналов. Имеется два класса обучающих методов: детерминистский и стохастический.
Детерминистский метод обучения шаг за шагом осуществляет процедуру коррекции весов сети, основанную на использовании их текущих значений, а также величин входов, фактических выходов и желаемых выходов. Обучение персептрона является примером подобного детерминистского метода.
Стохастические методы обучения выполняют псевдослучайные изменения величин весов, сохраняя те изменения, которые ведут к улучшениям. Чтобы показать это наглядно, рассмотрим рис. 7.1, на котором изображена типичная сеть, где нейроны соединены с помощью весов. Выход нейрона является здесь взвешенной суммой его входов, которая преобразована с помощью нелинейной функции. Для обучения сети могут быть использованы следующие процедуры:
Выбрать вес случайным образом и подкорректировать его на небольшое случайное число. Предъявить множество входов и вычислить получающиеся выходы.
Сравнить эти выходы с желаемыми выходами и вычислить величину разности между ними. Общепринятый метод состоит в нахождении разности между фактическим и желаемым выходами для каждого элемента обучаемой пары, возведение разностей в квадрат и нахождение суммы этих квадратов. Целью обучения является минимизация этой разности, часто называемой целевой функцией.
Выбрать вес случайным образом и подкорректировать его на небольшое случайное значение. Если коррекция помогает (уменьшает целевую функцию), то сохранить ее, в противном случае вернуться к первоначальному значению веса.
Повторять шаги с 1 по 3 до тех пор, пока сеть не будет обучена в достаточной степени.
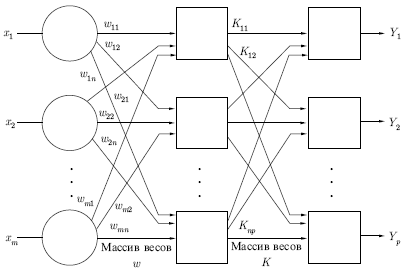
Рис. 7.1.
Этот процесс стремится минимизировать целевую функцию, но может попасть, как в ловушку, в неудачное решение. На рис. 7.2 показано, как это может происходить в системе с единственным весом. Допустим, что первоначально вес взят равным значению в точке А. Если случайные шаги по весу малы, то любые отклонения от точки А увеличивают целевую функцию и будут отвергнуты. Лучшее значение веса, принимаемое в точке В, никогда не будет найдено, и система будет поймана в ловушку локальным минимумом вместо глобального минимума в точке В. Если же случайные коррекции веса очень велики, то как точка А, так и точка В будут часто посещаться, но то же самое будет верно и для каждой другой точки. Вес будет меняться так резко, что он никогда не установится в желаемом минимуме.
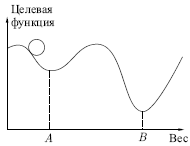
Рис. 7.2.
