
- •[Править]Замечание
- •Первая формулировка
- •[Править]Расширенный вариант первой формулировки
- •[Править]Вторая формулировка
- •Функциональные последовательности
- •Определения
- •Предел функции по Гейне
- •[Править]Предел функции по Коши
- •Определения Править
- •Бесконечно малые функции
- •Бесконечно большая функция
- •Определения
- •[Править]Односторонний предел по Гейне
- •[Править]Односторонний предел по Коши
- •[Править]Односторонний предел как предел вдоль фильтра
- •Свойства непрерывных функций. Непрерывность сложной функции
- •Точки разрыва функции
- •Формулировка
- •18.1. Сравнение бесконечно малых функций
Бесконечно большая функция
Расстановка ударений: БЕСКОНЕ`ЧНО БОЛЬША`Я ФУ`НКЦИЯ
БЕСКОНЕЧНО БОЛЬШАЯ ФУНКЦИЯ - функция переменного х, к-рая в данном процессе изменения х становится и остается по абсолютной величине больше любого наперед заданного числа. Точнее, функция f(x), определенная в окрестности точки х0, наз. бесконечно большой функцией при х, стремящемся к x0, если для любого числа М > 0 найдется такое число δ = δ (М) > 0, что для всех х ≠ х0 и таких, что |х - х0 | < δ, выполняется неравенство |f(x)| > M. Этот факт записывается так:
![]()
Аналогичным образом определяются
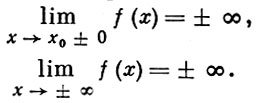
Напр.,
![]()
означает, что для любого М > 0 найдется такое δ = δ (M) > 0, что для всех z < - δ выполняется неравенство f(x) > M. Изучение Б. б. ф. может быть сведено к изучению бесконечно малых функций, т. к. если f(x) есть Б. б. ф., то функция ψ (х) = 1/f(x) является бесконечно малой.
Определения
Пусть
на некотором числовом множестве ![]() задана числовая
функция
задана числовая
функция ![]() и
число
и
число ![]() — предельная
точка области
определения
— предельная
точка области
определения ![]() .
Существуют различные определения для
односторонних пределов функции
в
точке
,
но все они эквивалентны.
.
Существуют различные определения для
односторонних пределов функции
в
точке
,
но все они эквивалентны.
[Править]Односторонний предел по Гейне
Число называется правосторонним пределом (правым пределом, пределом справа) функции в точке , если для всякой последовательности , состоящей из точек, больших числа , которая сама сходится к числу , соответствующая последовательность значений функции сходится к числу .
![]()
Число называется левосторонним пределом (левым пределом, пределом слева) функции в точке , если для всякой последовательности , состоящей из точек, меньших числа , которая сама сходится к числу , соответствующая последовательность значений функции сходится к числу .[1]
![]()
[Править]Односторонний предел по Коши
Число называется правосторонним пределом (правым пределом, пределом справа) функции в точке , если для всякого положительного числа
 отыщется
отвечающее ему положительное
число
отыщется
отвечающее ему положительное
число 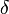 такое,
что для всех
точек
изинтервала
такое,
что для всех
точек
изинтервала 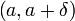 справедливо неравенство
.
справедливо неравенство
.
![]()
Число называется левосторонним пределом (левым пределом, пределом слева) функции в точке , если для всякого положительного числа отыщется отвечающее ему положительное число такое, что для всех точек из интервала
 справедливо
неравенство
.[1]
справедливо
неравенство
.[1]
![]()
[Править]Односторонний предел как предел вдоль фильтра
Односторонний
предел является частным случаем общего
понятия предела
функции вдоль фильтра.
Пусть ![]() и
и ![]() Тогда
системы множеств
Тогда
системы множеств
![]()
и
![]()
являются фильтрами. Пределы вдоль этих фильтров совпадают с соответствующими односторонними пределами:
![]()
![]()
Связь предела с односторонними пределами
f(x) определена на (a,b) за исключением, быть может, точки x0(a,b) .
Теорема.
Для того, чтобы существовал предел ![]() ,
(A – число) н. и д. существование
односторонних пределов и их равенство
числу A.
,
(A – число) н. и д. существование
односторонних пределов и их равенство
числу A.
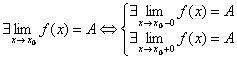
Доказательство: Следует непосредственно из определения.
Замечание Теорема верна и для A=+ ,-, но формально не верна для A=.
Пример:
f(x)=1/x, x0=0, ![]()
Определение. Функция ![]() ,
определенная на множестве
,
определенная на множестве ![]() называется
непрерывной в точке
называется
непрерывной в точке ![]() ,
если
,
если ![]() .
.
Фу́нкция
Дирихле́ — функция ![]() ,
принимающая значение 0, если аргумент
есть рациональное
число,
и значение 1, если аргумент есть иррациональное
число,
,
принимающая значение 0, если аргумент
есть рациональное
число,
и значение 1, если аргумент есть иррациональное
число,
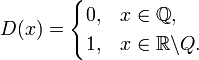
Так как функция разрывна в каждой точке (между любыми двумя рациональными числами есть хотя бы одно иррациональное), то её график нарисовать невозможно, но мысленно можно представить.
Так как в любой окрестности любой точки вещественной прямой содержатся как рациональные, так и иррациональные числа (а значит, как нули, так и единицы функции), ни в одной точке у D(x) нет предела, а значит, она разрывна на всей числовой прямой, причём все точки разрыва — второго рода.
Функция Дирихле применяется в теории вероятностей и математической статистике.
Названа в честь немецкого математика Дирихле.
Первый замечательный предел:
![]()
Теорема. Если две функции![]() и
и![]() определены в одном и том же
промежутке
определены в одном и том же
промежутке
![]() и обе непрерывны в точке
и обе непрерывны в точке![]() то
в той же точке будут непрерывны и функции
то
в той же точке будут непрерывны и функции
![]()
(последняя — при условии, что![]()
Сложная функция – функция от функции. Если z – функция от у, т.е. z(y), а у, в свою очередь, – функция от х, т.е. у(х), то функция f(x) = z(y(x)) называется сложной функцией (или композицией, или суперпозицией функций) от х.
В такой функции х – независимая, а у – промежуточная переменная. При этом сложная функция определена для тех значений независимой переменной, для которых значения промежуточной функции у входят в область определения функции z(y).
Производная дифференцируемой сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточной функции по независимому аргументу:
![]() .
.
Эта формула легко распространяется на случай, когда у сложной функции имеется два, три и более промежуточных аргументов («цепное правило»): если z = f1(y1),y1 = f2(y2), …, yn-1 = fn(x), то
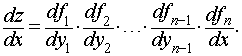

![]()
![]()
![]()
![]()
![]()
