10.5 Проверка значимости корреляционной связи с помощью дисперсионного анализа

Для определения тесноты связи между факторным и результативным признаком используются:

1) индекс корреляции R, вычисляемый по формуле

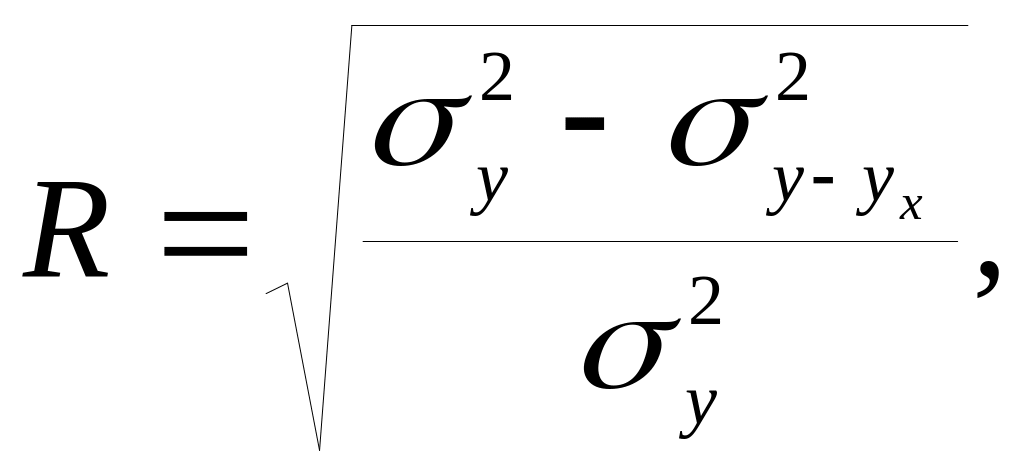
где − общая дисперсия,

− дисперсия, измеряющая отклонение y от y_x .

Значение R меняется от 0 до 1. Чем ближе к 1, тем связь теснее. Применяется для любого вида связи (не показывает направления).

2) теоретическое корреляционное отношение η:

Частным случаем теоретического корреляционного отношения является линейный коэффициент корреляции ( ), который применяется только в случае линейной связи. Он меняется от −1 до 1, показывает не только тесноту, но и направление связи. Вычисляется по следующей формуле:

.

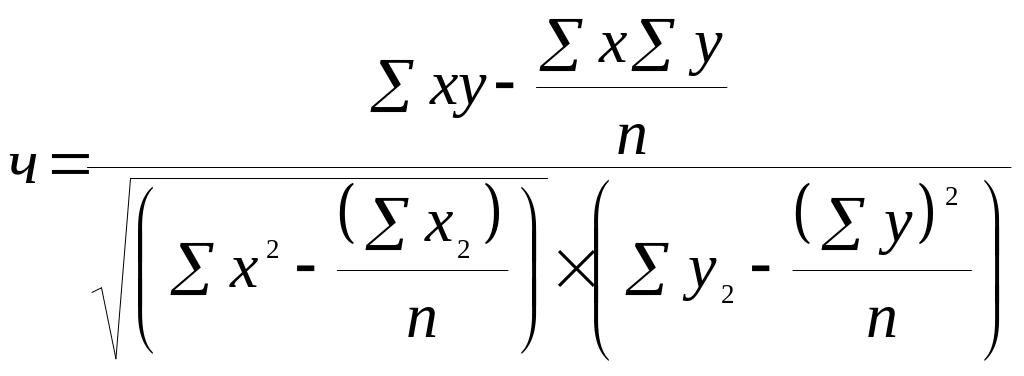10.6 Понятие о многофакторном корреляционно-регрессионном анализе

Для многофакторного корреляционного анализа математически задача формулируется следующим образом: требуется найти аналитическое выражение, наилучшим образом отражающее связь между факторными признаками и результативными:

у=f(x₁, x₂ ,. . . x_n).

Наиболее сложным представляется выбор формы связи, т. к. графический метод здесь неприемлем. Можно опираться на теоретические знания, на опыт предыдущих исследований, а при отсутствии таких сведений можно определить вид связи опытным путем, т. е. путем перебора функций разных видов. Однако это сопряжено с большим количеством лишних расчетов.

Поскольку любую функцию многих переменных можно свести к линейному виду, то уравнение множественной регрессии можно искать в линейной форме:

.

Каждый коэффициент этого уравнения, кроме а₀, показывает степень влияния соответствующего фактора на анализируемый показатель (при фиксированном положении на среднем уровне остальных факторов), и все эти коэффициенты называются коэффициентами регрессии и показывают, как меняется результативный признак при изменении соответствующего факторного на 1. Чтобы определить, какие из факторов оказывают наибольшее влияние, вычисляют коэффициенты эластичности:

Они показывают, на сколько процентов изменится величина результативного признака при изменении соответствующего факторного признака на 1 %.

Литература

1. Теория статистики: учеб. / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 1998. – 576 с.

2. Экономическая статистика: учебник / Под ред. Ю.Н.Иванова. – М.: ИНФРА-М, 1998. – 480 с.

3. Статистика: курс лекций / Харченко Л.П., Долженкова В.П., Ионин В.Г. и др.; под ред. к.э.н. В.Г. Ионина. – Новосибирск: Издательство НГАЭ и У. – М.: ИНФРА-М, 1999. – 310 с.

4. Практикум по теории статистики: учеб. пособие / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 1999. – 416 с.

5. Практикум по статистике: учеб. пособие для вузов / Под ред. В.М. Симчеры / ВЗФЭИ – М.: ЗАО «Финстатинформ», 1999. – 259 с.

6. Сиденко А.В., Попов Г.Ю., Матвеев В.М. Статистика: учебник. – М.: Издательство «Дело и сервис», 2000. – 464 с.