8.3 Темпы роста, их вычисление

Темпы роста − это отношение уровней ряда одного периода к другому.

Темпы роста могут быть вычислены как базисные, когда все уровни ряда относятся к уровню одного и того же периода базисного, и как цепные, если в знаменателе отношения стоит уровень предыдущего периода.

Обозначение:

Т_р= y_i/y₀ − базисный,

Т_р= y_i/y_i-1 − цепной.

Темпы роста могут быть выражены в виде коэффициента или процента.

Базисные темпы роста характеризуют непрерывную линию развития, а цепные − интенсивность развития в каждом отдельном периоде, причём произведение цепных темпов равна темпу базисному. А частное от деления базисных темпов равно промежуточному цепному.

8.4 Прирост и темп прироста

Различают понятие абсолютного и относительного прироста. Абсолютный прирост вычисляют как разность уровней ряда и выражают в единицах измерения показателей ряда.

Если из последующего уровня вычитается предыдущий, то мы имеем цепной абсолютный прирост.

Если из каждого уровня вычитается один и тот же уровень − базисный, то это базисный абсолютный прирост.

Средний абсолютный прирост вычисляется двумя способами:

1) Как средняя арифметическая простая годовых (цепных) приростов, т.е.

.

2) Как частное от деления базисного прироста к числу периодов:

.

Относительную оценку значения абсолютного прироста по сравнению с первоначальным уровнем дают показатели темпа прироста (Т_∆ⁱ). Его определяют двумя способами:

1. Как отношение абсолютного прироста (цепного) к предыдущему уровню:

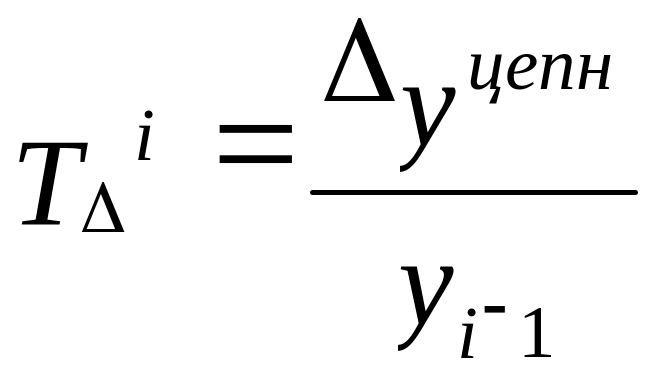
Это цепной темп прироста.

Как отношение базисного абсолютного прироста к базисному уровню:

Это базисный темп прироста.

2) Как разница между темпом роста и единицей, если темп роста выражен в виде коэффициента:

Т_∆ = Т_р-1, или

Т_∆ = Т_р- 100, если темп роста выражен в процентах.

Темп прироста показывает, на сколько процентов увеличились размеры явления за изучаемый период. Если темп прироста имеет знак минус, то говорят о темпах снижения.

Абсолютное значение 1-го процента прироста равно отношению абсолютного прироста (цепного) к цепному темпу прироста, выраженному в процентах:

.

Этот показатель можно также вычислить как одну сотую часть предыдущего уровня:

А_i = 0,01хУ_i;

Расчет среднего абсолютного значения 1% прироста за несколько лет производится по формуле простой средней арифметической:

8.5 Вычисление средних темпов роста и прироста

При вычислении среднегодового темпа роста нельзя применять простую среднюю арифметическую, т. к. сумма годовых темпов не будет иметь смысла. В этом случае применяют среднюю геометрическую, т. е.:

где Тр_i − годовые цепные темпы роста,

n − число темпов.

Поскольку произведение цепных темпов равно темпу базисному, то средний темп роста может быть рассчитан следующим образом:

Error: Reference source not found

При расчёте по этой формуле не следует знать годовые темпы роста. Величина среднего темпа будет зависеть от соотношения начального и конечного уровня ряда.

8.6 Приемы анализа рядов динамики

Для исследования закономерностей динамики социально-экономических процессов изучают общую линию развития, или так называемый тренд.

Изменение уровня ряда динамики обусловлено влиянием различных факторов. Постоянно влияющие факторы оказывают на изучаемое явление определяющее воздействие и формируют тренд.

Другие факторы действуют периодически, что вызывает колебание уровней ряда динамики, и основная тенденция развития сразу не видна. Для выявления тренда применяют ряд методов.

Методы, традиционно применяемые для выявления временных тенденций в изменении экономических показателей, можно разделить на две большие группы. Это методы «механического сглаживания» и «аналитического выравнивания». К первой группе относят простые приемы укрупнения временных интервалов и расчета скользящей средней, во вторую входят более сложные методы, основанные на геометрическом представлении динамических данных и использовании надежных теоретических моделей тренда.

Отличительными чертами методов механического сглаживания являются простота расчетов, наглядность аналитических результатов, однако неизбежным при использовании этого метода является потеря некоторого числа уровней динамического ряда, отсутствие сколько-нибудь надежного критерия выбора промежутка сглаживания, невозможность формально описать, а значит, прогнозировать тренд.

Пример 1. Применение метода укрупнения интервалов. Известны данные о размерах прибыли коммерческой фирмы за 15 последних месяцев (табл. 8.1). Необходимо выяснить, какова общая тенденция финансовых результатов деятельности фирмы.

Первоначально представленные в таблице фактические данные о размерах прибыли за каждый месяц не позволяли выявить какую-либо тенденцию. Выбран укрупненный трехмесячный интервал. После суммирования значений анализируемого показателя по периодам продолжительностью в три месяца и последующего вычисления средних за квартал значений установлено, что размер прибыли имеет общую тенденцию к снижению.

Таблица 8.1 − Размеры прибыли коммерческой фирмы за 15 месяцев

Месяц	Прибыль балансовая, тыс.руб.	Сумма прибыли за три месяца, тыс.руб.	Средний размер прибыли за месяц, тыс.руб. (гр.3/3)
1	2	3	4
01	66	-	-
02	68	214	71,3
03	80	-	-
04	74	-	-
05	66	211	70,
06	71	-	-
07	78	-	-
08	63	210	70
09	69	-	-
10	65	-	-
11	67	204	68
12	72	-	-
01	68	-	-
02	64	203	67,7
03	71	-	-
Итого:	1042	1042	69,5

Как видно в ходе расчетов, из пятнадцати уровней динамического ряда осталось всего пять, десять уровней потеряно.

Предложенную задачу можно решить вторым способом: с применением скользящей средней. Для анализа берутся трехмесячные периоды сглаживания.

Расчеты и результаты представлены в табл. 8.2.

Таблица 8.2 − Прибыль коммерческой фирмы за 15 месяцев

Месяц		Прибыль балансовая, тыс. р.		Сумма прибыли по месяцам, тыс. р.		Средний месячный размер прибыли, тыс.руб.
1		2		3		4
01		66		-		-
02		68		214		71,3
03		80		222		74,0
04		74		220		73,3
05		66		211		70,3
06		71		215		71,7
0,7		78		212		70,7
0,8	63		210		70,0
0,9	69		197		65,7
10	65		201		67,0
11	67		204		68,0
12	72		207		69,0
01	68		204		68,0
02	64		203		67,7
03	71		-		-
Итого	1042		-		69,5

При расчете скользящей средней первая трехмесячная сумма рассчитывается из первых трех элементов динамического ряда, вторая и все последующие суммы – сдвигаясь только на одно число по динамическому ряду вниз. Утрачиваются только два элемента ряда − одно верхнее и одно нижнее значения. В данном случае общее число утраченных уровней ряда будет зависеть от периода сглаживания.

Как видно из таблицы, значения скользящей средней подтверждают ранее сделанный вывод о снижении среднего за месяц размера прибыли.

В наших примерах при расчете скользящей средней период сглаживания включал нечетное число месяцев (3, 5, 7). Однако использоваться может и четное число месяцев (лет) (2, 4, 6 ...). Тогда за период сглаживания вначале рассчитывают промежуточные суммы значений уровней и, например, если сглаживание происходит за 2 месяца (года), первая промежуточная сумма будет расположена между первым и вторым уровнями ряда, вторая сумма − между вторым и третьим уровнями и т.д. Затем эти суммы центрируются и вычисляется скользящая средняя. Центрирование означает расчет средней из двух промежуточных сумм, и для нашего примера первая центрированная сумма будет расположена напротив второго уровня ряда, вторая центрированная сумма − напротив третьего уровня ряда и т.д.