4.3 Основные принципы построения относительных величин
Основными принципами построения относительных величин являются:
Сравниваемые абсолютные показатели должны быть чем-то связаны в реальной жизни объективно, независимо от нашего желания.
При построении относительной величины сравниваемые показатели должны отличаться только одним признаком или одним атрибутом.
Необходимо знать возможные границы существования относительного показателя. Если исходные показатели в текущем периоде и базисном периоде имеют равные знаки, то построение относительных показателей для них невозможно.
4.4 Построение системы статистических показателей
Поскольку отдельные свойства объекта или явления не изолированы, а связаны между собой, то и статистические показатели, отражающие эти свойства объекта, необходимо связывать в систему.
Виды таких систем довольно разнообразны и зависят от решаемых задач и от сложности изучаемых явлений. Они могут включать показатели как функционально несвязанные, так и функционально связанные.
Основные требования к системам – чтобы они обязательно включали абсолютные и относительные показатели.
5 Средние величины
5.1 Понятие средней величины. Виды средних величин
Средние величины – наиболее распространенные обобщающие величины в статистике.
Средней величиной называется обобщающая характеристика совокупности однотипных явлений по какому-либо количественно-варьирующему признаку в расчете на единицу совокупности в конкретных условиях места и времени.
Такие средние величины, которые обобщают качественно однородные совокупности, называют типическими средними величинами.
На практике часто приходится рассматривать качественно неоднородные совокупности и рассчитывать их обобщающую среднюю величину.
Пример: средняя величина национального дохода на душу населения, среднее потребление продуктов и т.д. Такого типа средние называются системными средними.
Для того, чтобы средняя характеристика была достоверной величиной, необходимо, чтобы ее построение было основано на массовом обобщении фактов.
Основная масса средних величин, которые рассматриваются в статистике, относится к классу так называемых степенных средних.
Общая их формула имеет вид:
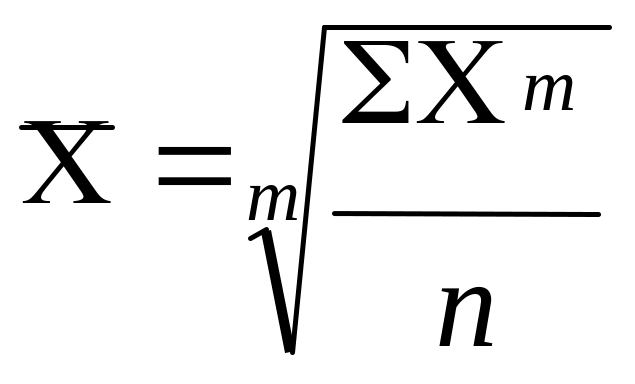
где n – число единиц совокупности,
m – показатель степени.
В зависимости от этого показателя рассматриваются различные виды средних:
1)
m=1,
–
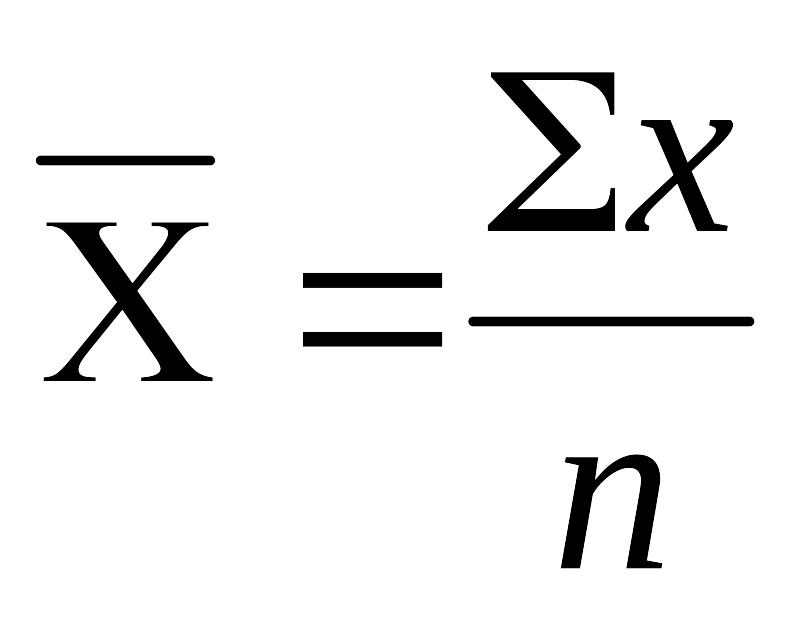средняя арифметическая;
2)
m=2,
–
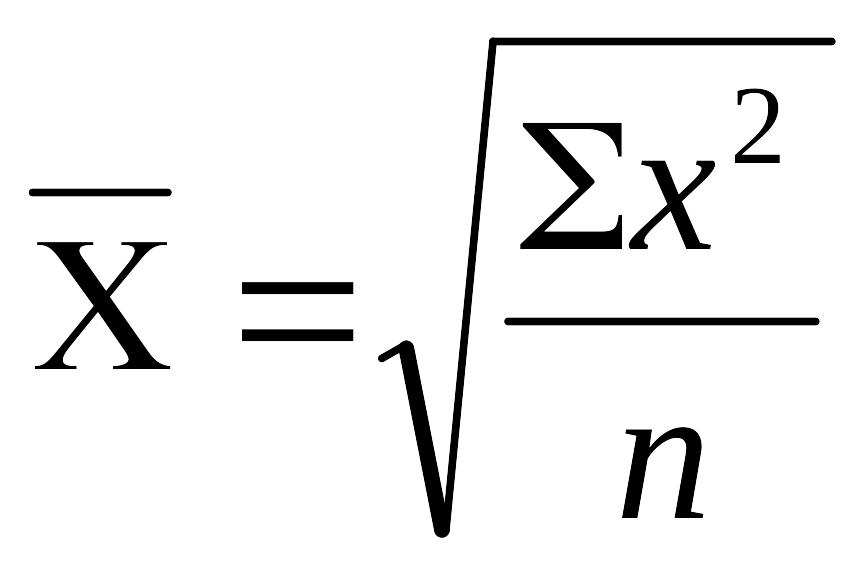средняя квадратическая;
3)
m=3,
–
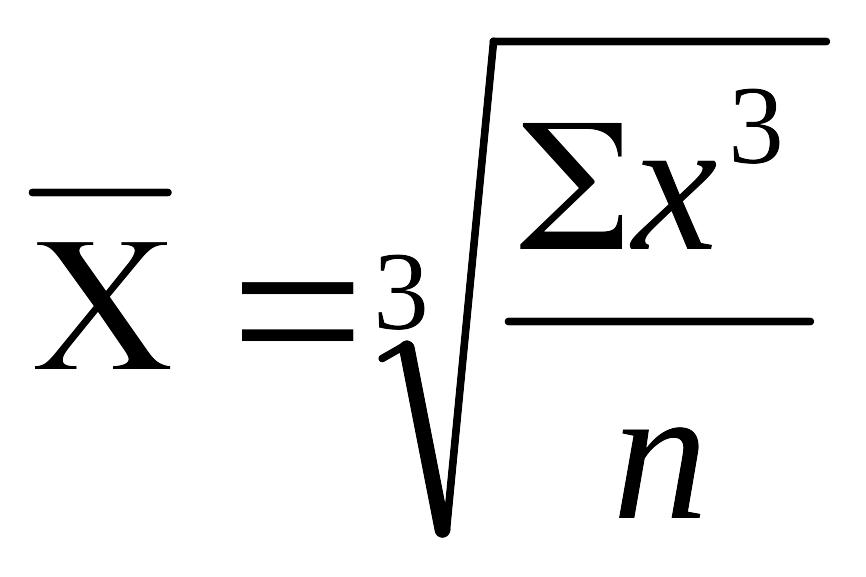средняя кубическая;
4)
m=
-1,
–
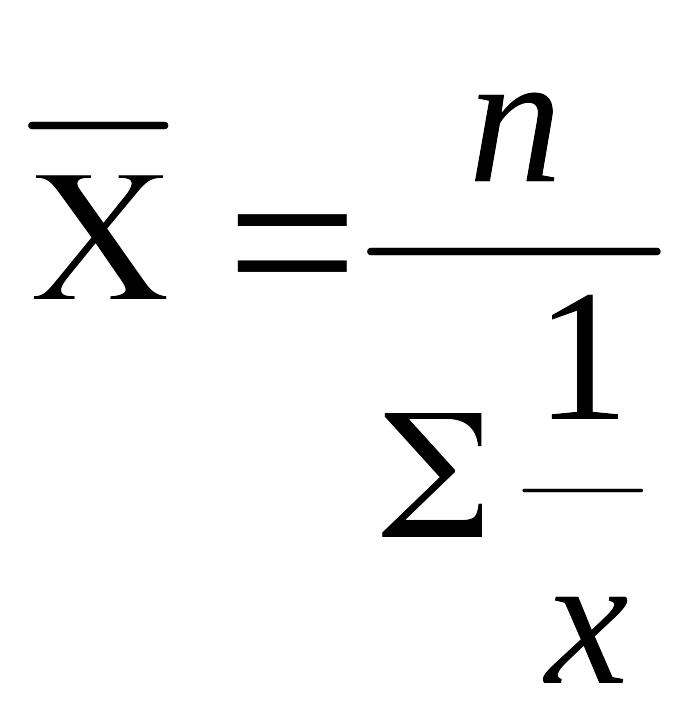средняя гармоническая;
5)
m=0,
–
средняя геометрическая.
Чем выше показатель степени, тем выше значение средней. Такое свойство называют свойством мажорантности средних.
5.2 Средняя арифметическая, ее свойства и вычисление
Средняя арифметическая используется в двух формах:
а) в форме простой:
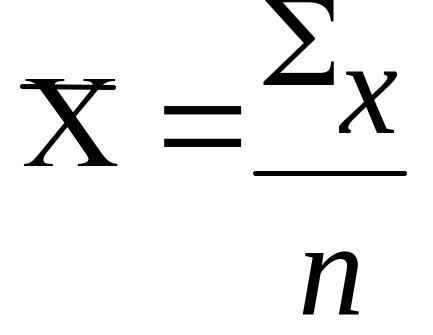
(5.1)
б) в форме средней арифметической взвешенной:
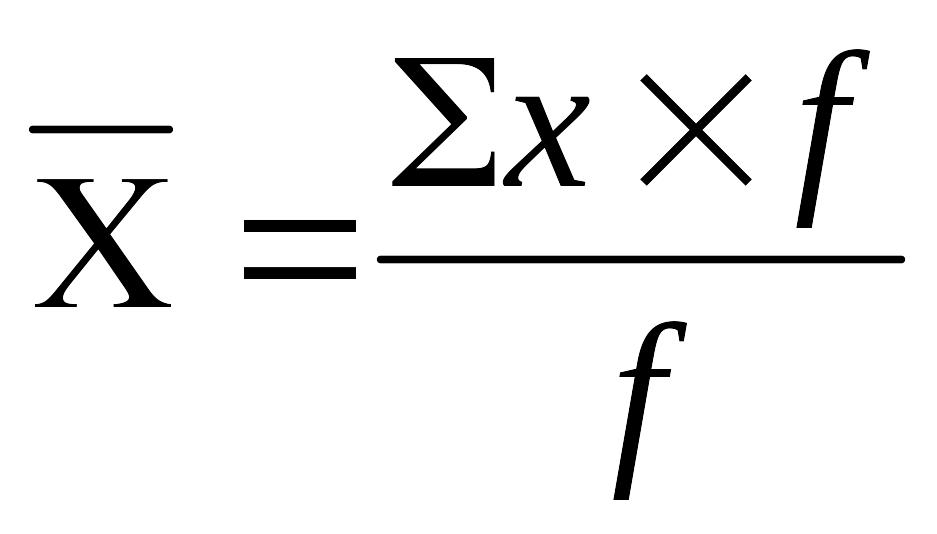
(5.2)
Формула (5.1) применяется тогда, когда все частоты равны 1 или равны между собой. Во всех остальных случаях применяется формула (5.2).
Свойства средней арифметической:
Произведение средней арифметической на сумму частот равно сумме произведения вариант на частоты:
.
2. Если к каждой варианте прибавить (или отнять) какое-либо постоянное число, то средняя увеличится (или уменьшится) на такое же число:
3. Если каждую варианту разделить (умножить) на какое-либо число А≠0, то средняя уменьшится (увеличится) во столько же раз:
4. Если частоты разделить или умножить на какое-либо не равное 0 число, то средняя не изменится.
Учитывая свойства средней арифметической, в формулы (5.1) и (5.2) для вычисления средней можно подставить вместо частот частости.
5. Сумма отклонений вариант от их средних арифметических равна 0:
Пример: Вычисление средней в дискретном ряду
Стаж, лет Х |
Число рабочих, чел. f |
X·f |
1 |
2 |
2 |
2 |
3 |
6 |
3 |
2 |
6 |
4 |
5 |
20 |
5 |
1 |
5 |
ИТОГО |
13 |
39 |
Пример 2. Вычисление средней в интервальном ряду:
Группы рабочих по размеру месячной оплаты труда, тыс.руб. |
Число рабочих, чел. f |
X |
X·f |
1 |
2 |
3 |
4 |
До 120 |
10 |
115 |
1150 |
120-130 |
30 |
125 |
3750 |
130-140 |
50 |
135 |
6750 |
140-150 |
60 |
145 |
8700 |
150-160 |
145 |
155 |
22475 |
160-170 |
110 |
165 |
18150 |
1 |
2 |
3 |
4 |
170-180 |
80 |
175 |
14000 |
свыше 180 |
15 |
185 |
2775 |
Итого: |
500 |
|
77750 |
Найти среднюю заработную плату.
Чтобы вычислить среднюю в интервальном вариационном ряду, нужно перейти от интервального к дискретному, взяв в качестве вариант середины интервала. Так как первый интервал открытый, то считаем, что он такой же по величине, как последующий, а последний − такой же, как предыдущий.
1-й интервал: (110+1020)/2=115 и т.д.
Для исчисления средней воспользуемся формулой (5.2):
