
- •Глава 2. Дифференциальная геометрия 15
- •1.1. Интеграл Римана на n-мерном промежутке
- •Кратный интеграл.
- •Теорема 1. Необходимое условие интегрируемости по Риману
- •Мера Лебега
- •Критерий Дарбу интегрируемости функции по Риману. Верхние и нижние суммы Дарбу.
- •Лекция 2
- •1.2. Интеграл по множеству. Допустимые множества
- •Общие свойства интеграла
- •Линейность
- •2. Аддитивность
- •3. Оценка интеграла
- •Лекция 3 Сведение кратного интеграла к повторному. Теорема Фубини
- •Замена переменных в кратном интеграле. Формула Грина.
- •Лекция 4 Геометрический смысл модуля якобиана отображения
- •1.3. Приложения кратных интегралов
- •Лекция 5
- •1.4. Несобственные кратные интегралы
- •Несобственные кратные интегралы от неотрицательных функций
- •Касательная к кривой
- •Длина кривой. Спрямляемая кривая. Натуральная параметризация
- •Основной трёхгранник кривой. Формулы Френе
- •Формулы Френе.
- •Геометрический смысл величин k и æ
- •Вид кривой вблизи произвольной точки
- •2.2. Поверхность в Евклидовом пространстве
- •Ориентация поверхности.
- •Край поверхности и его ориентация.
- •Согласование ориентации поверхности и её края
- •Касательное пространство к поверхности
- •Касательная к поверхности в
- •Площадь поверхности в Евклидовом пространстве
- •Алгебра кососимметрических форм
- •3.2. Дифференциальные формы
- •Координатная запись дифференциальной формы
- •3.3. Дифференциальные операторы векторного анализа. Их связь с дифференциальными формами
- •Перенос форм при отображениях
- •Координатная запись форм, возникающих при переносе.
- •Глава 4. Криволинейные и поверхностные интегралы.
- •4.1. Интегралы от формы работы, потока. Форма объёма
- •4.2. Интегралы I и II рода.
- •Общая формула Стокса
- •Глава 5. Элементы векторного анализа
- •5.1. Дифференциальные операции векторного анализа
- •5.2. Потенциальные поля
- •Замкнутые и точные формы
- •5.3. Соленоидальные поля
Алгебра кососимметрических форм
Опр.:
1. Форма
![]() называется кососимметрической, если:
называется кососимметрической, если:
![]()
2.
![]() - подпространство кососимметрических
форм размерности
- подпространство кососимметрических
форм размерности
Пример:
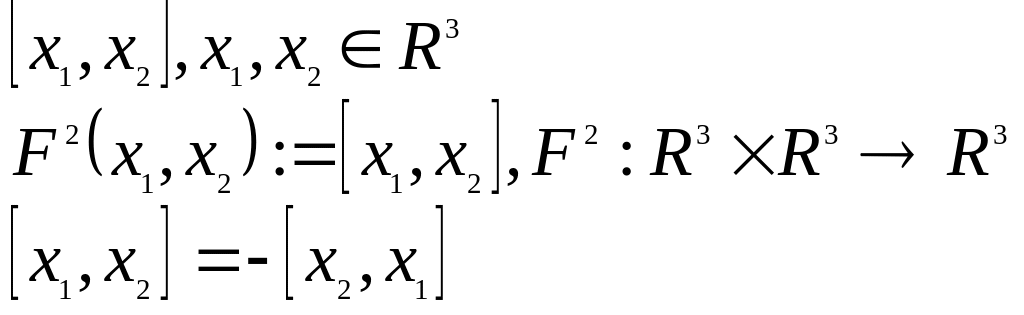
Альтернирование форм
Опр.:
- форма размерности
Оператор
![]() называется оператором альтернирования,
если:
называется оператором альтернирования,
если:
![]()
![]()
Утв.:
Если:
![]()
То:
![]() - Операция альтернирования переводит
кососимметрическую форму саму в себя.
- Операция альтернирования переводит
кососимметрическую форму саму в себя.
Свойства:
1.
![]()
2.
![]()
Пример:
1.
![]()
2. а)
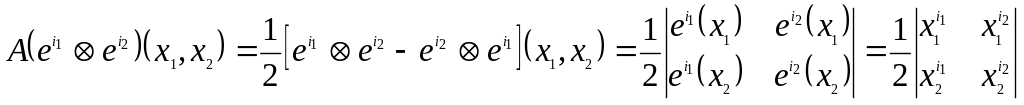
б)
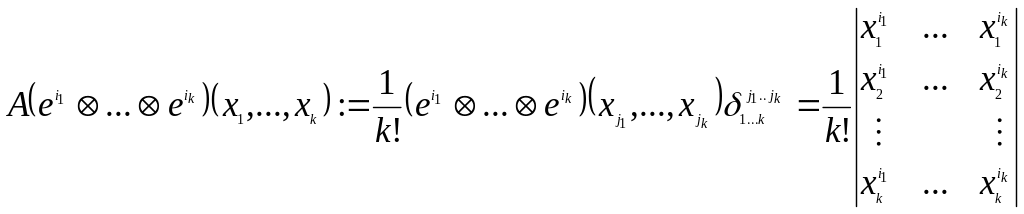
Опр.:

Операция
![]() - внешнее произведение.
- внешнее произведение.
Пример:
1.
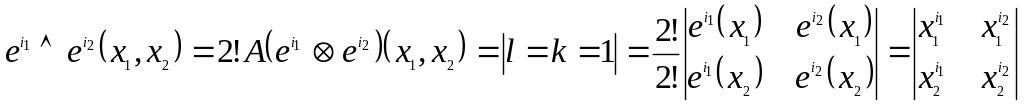
2.
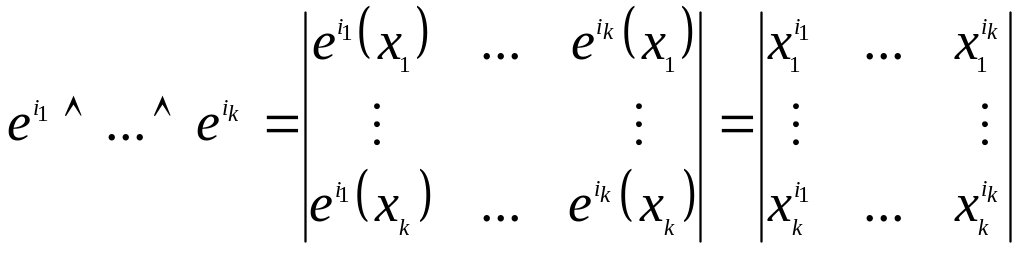
3.
![]() -
-
![]() 1-форма
1-форма
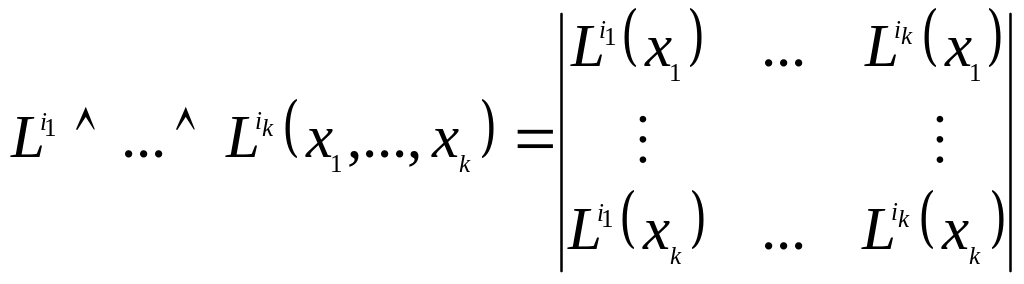
Свойства:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
Координатная запись кососимметрической формы.
Утв.:
Если:
![]() - кососимметрическая форма
- кососимметрическая форма
То:
![]()
Док-во:
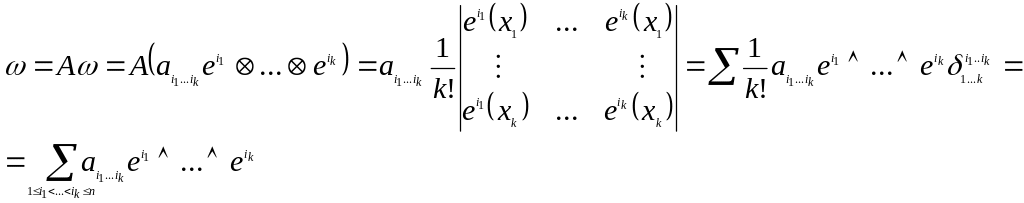
Следствие:
Т.к.
![]() ,
то
,
то
![]()
Замечание
Множество кососимметрических форм
![]() является градуированной алгеброй.
является градуированной алгеброй.
![]()
![]()
![]()
Замечание
1. В силу определения кососимметрической формы, она равна нулю, если в ней есть одинаковые элементы.
2.
![]()
Лекция 13
3.2. Дифференциальные формы
Опр.:
1. В области
![]() задана вещественнозначная дифференциальная
задана вещественнозначная дифференциальная
![]() -форма
,
если
-форма
,
если
![]() определена кососимметрическая форма
определена кососимметрическая форма
![]()
2. - порядок (степень) дифференциальной формы .
Пример:
1.
![]()
![]()
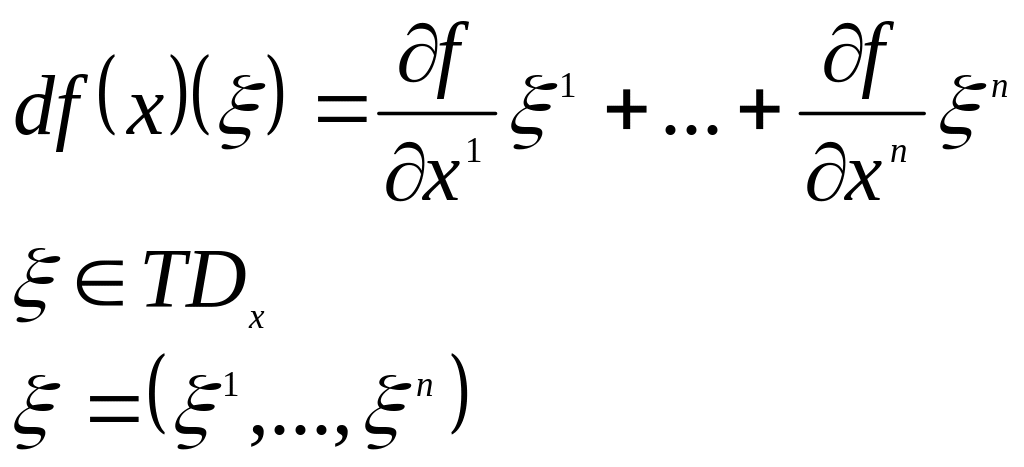
Т.о., дифференциал функции в точке – её 1-форма (линейная форма).
![]()
![]() -простейшая
дифференциальная форма
-простейшая
дифференциальная форма
2. а)
![]() - непрерывное векторное поле
- непрерывное векторное поле
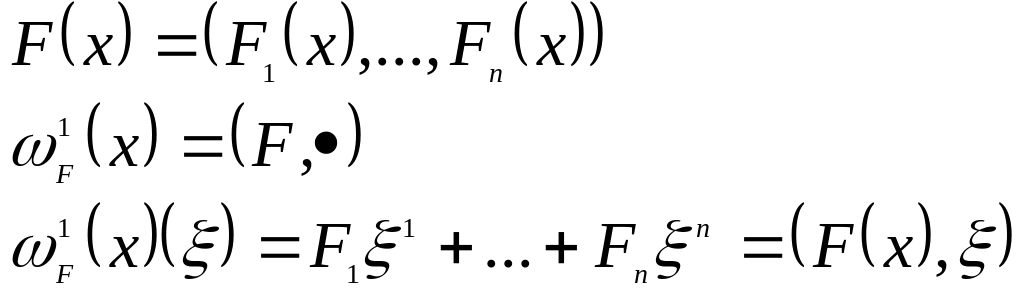
б)
![]()
- силовое поле,
![]()
![]()
Опр.:
![]() - форма работы.
- форма работы.
Координатная запись дифференциальной формы
Утв.:
Если:
![]() - простейшая дифференциальная форма
- простейшая дифференциальная форма
![]()
То:
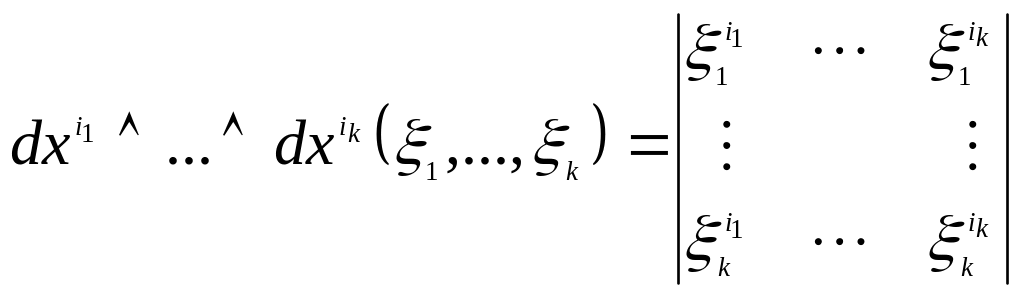
координатная запись простейшей - формы.
Координатная запись кососимметрической формы.
Утв.:
Если: - кососимметрическая форма,
То:
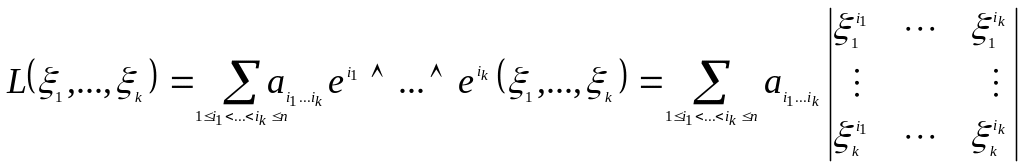
Координатная запись дифференциальной формы.
Утв.:
Если: -дифференциальная форма
То:
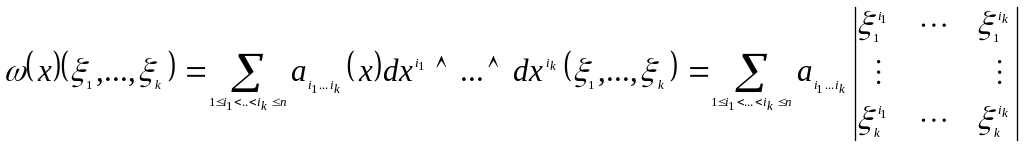
Т.о., произвольная дифференциальная -форма есть линейная комбинация простейших дифференциальных форм.
Пример:
![]()
Задача: посчитать значение
на векторах
![]() .
.
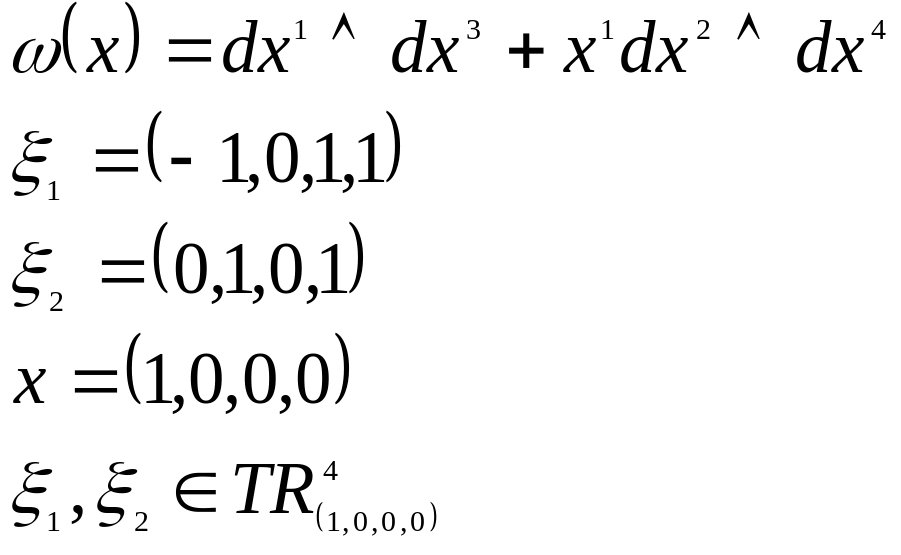
![]()
Пример:
![]() - векторное поле.
- векторное поле.
![]()
Строим параллелепипед на этих векторах. Ориентированный объём этого параллелепипеда – определитель из координат этих векторов. Разложив его по 1-й строке, получаем:
![]()
где
![]() обозначает отсутствие
обозначает отсутствие
![]() .
.
Форма потока:
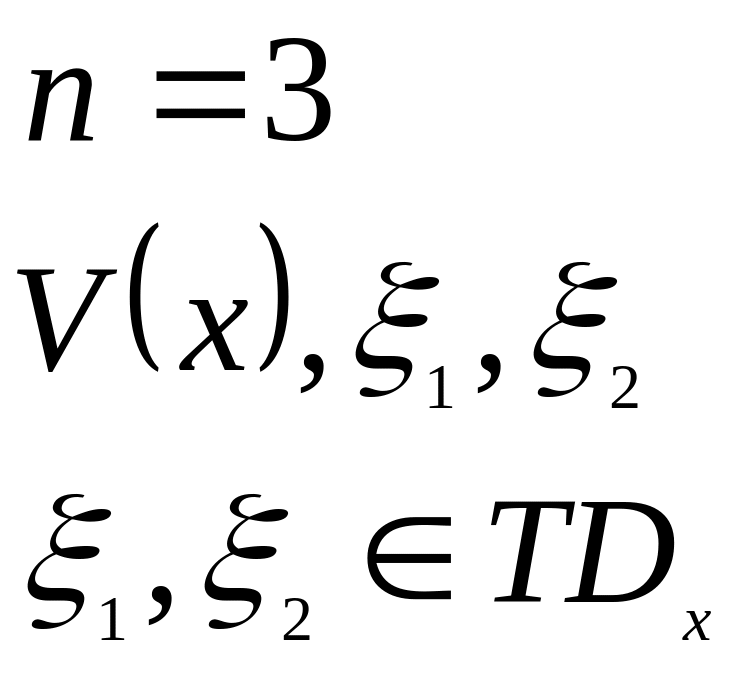
![]() -форма
потока.
-форма
потока.
Если - скорость течения жидкости, протекающей через площадку, натянутую на векторы за единицу времени.
![]()
Дифференциал формы.
Опр.:
![]() - пространство
-форм
гладкости
- пространство
-форм
гладкости
![]() - пространство
-форм
гладкости
- пространство
-форм
гладкости
![]() .
.
Опр.:
Внешним дифференциалом называется
линейный оператор
![]() ,
если:
,
если:
1) если
-функция
(![]() ,
функция – это 0-форма), то
,
функция – это 0-форма), то
![]() -обычный
дифференциал функции.
-обычный
дифференциал функции.
2)
![]()
3)
![]()
Координатное представление внешнего дифференциала.
Утв.:
Если:
![]()
То:
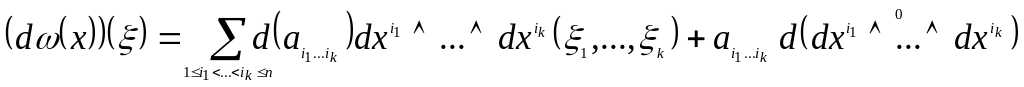
Т.о. при дифференцировании формы нужно продифференцировать её коэффициенты.
Пример 1:
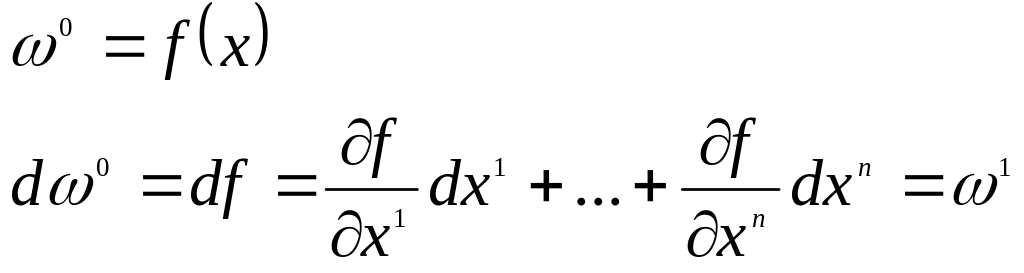
Пример 2:
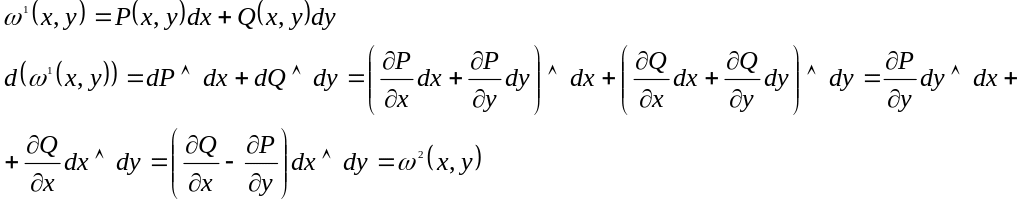
Лекция 14
3.3. Дифференциальные операторы векторного анализа. Их связь с дифференциальными формами
Определения 1:
![]()
Опр.: градиент
![]() - скалярная функция
- скалярная функция
![]()
Опр.: ротор
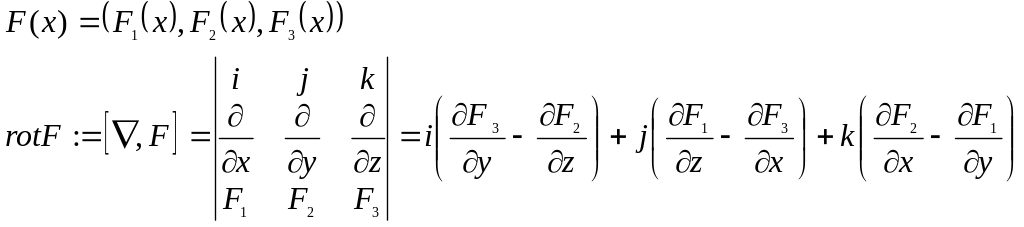
Опр.: дивергенция
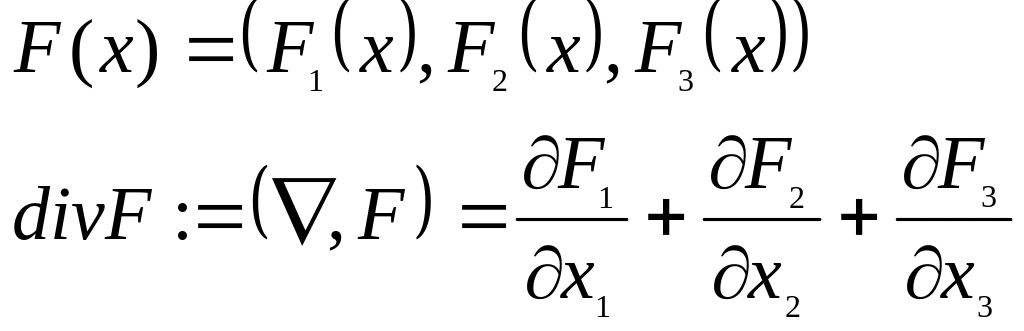
Опр.:
1.
![]()
![]()
2.
![]()
![]()
3.
![]() ,
-скалярная функция
,
-скалярная функция
![]()
Определения 2:
Градиент:
![]()
![]() - функция, соответствующая форме
- функция, соответствующая форме
![]()
Ротор:
![]()
![]() -функция,
соответствующая форме
-функция,
соответствующая форме
![]()
![]()
Дивергенция:
![]()
![]() - функция, соответствующая форме
- функция, соответствующая форме
![]()
![]()
Утв: Определения 1 и определения 2 эквивалентны.
Док-во:
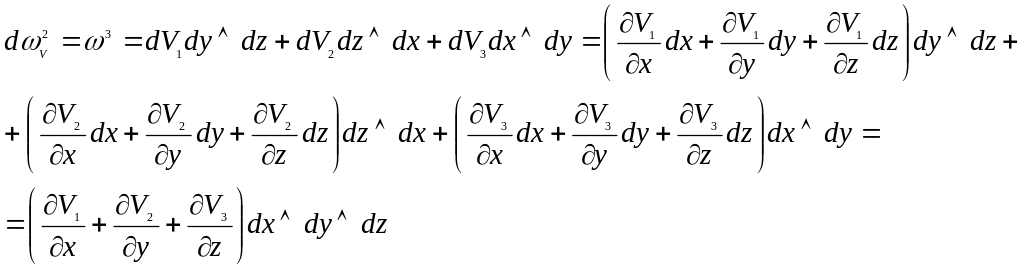
Лекция 15
