Лекция 3 Сведение кратного интеграла к повторному. Теорема Фубини
Теорема 2 (Фубини).
Если:
,
-
-мерный
интервал,
-
-мерный
интервал,
,
,
.
То:
.
Доказательство.
Строим разбиение интервалов
выбираем отмеченные точки
.
для почти всех
для почти всех
.
Если этой функции
не существует, то можно выбрать любое
значение из промежутка между верхней
и нижней суммой.
Следствие 7.
почти для всех
Следствие 8.
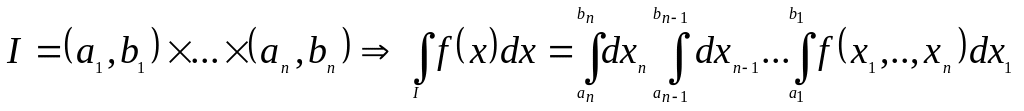
Следствие 9.
Если:
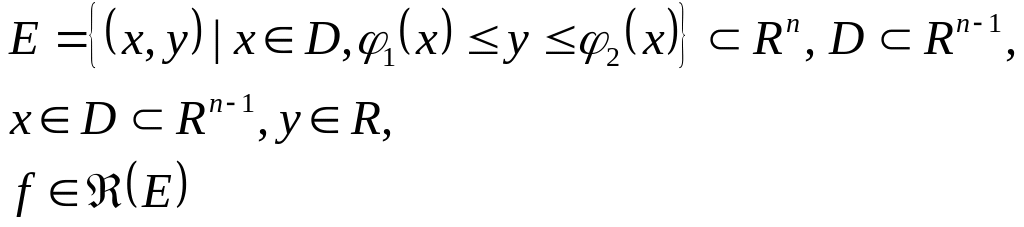
То:
.
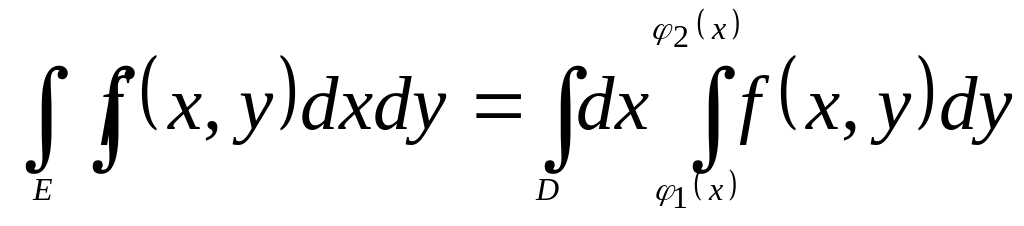Доказательство.
.
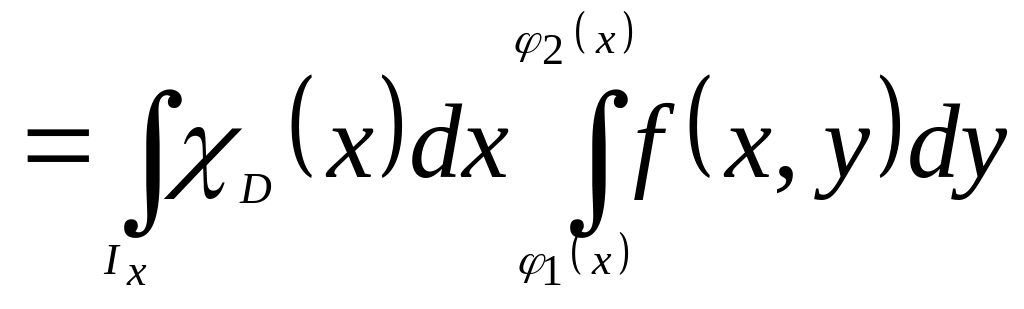Следствие 10.
Если: в условиях следствия 9 множество
измеримо по Жордану, а функции
непрерывны.
То: множество
имеет меру:
.
Замена переменных в кратном интеграле. Формула Грина.
Определение 7.
,
- гладкие функции,
- параметризованная кривая. Если
- замкнутая кривая (контур), то:
- прохождение контура против часовой
стрелки (положительная ориентация);
- прохождение контура по часовой стрелке
(отрицательная ориентация).
Определение 8.
.
Определение 9.
Область
называется элементарной, если:
.
Лемма 3. Формула Грина. Если: - элементарная область,
- кусочно-гладкая,
,
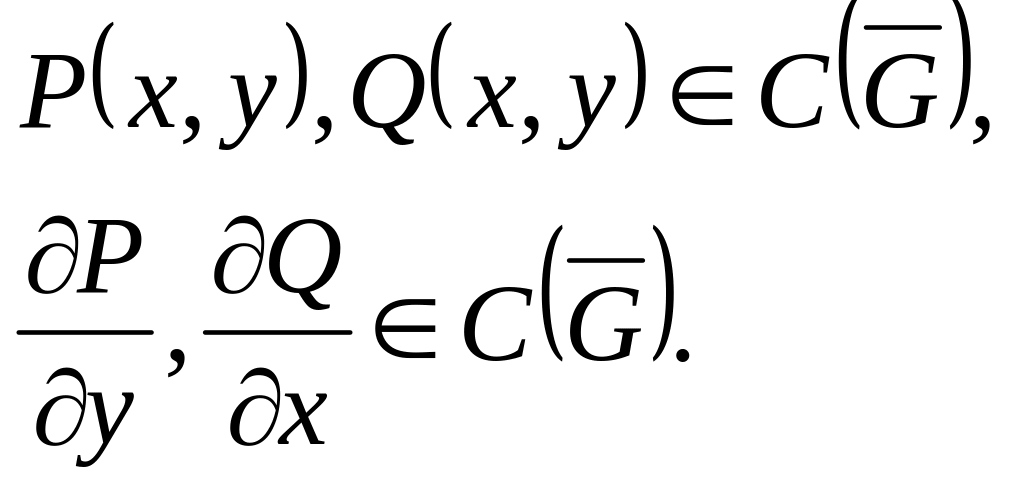
То:
,
.
Док-во:
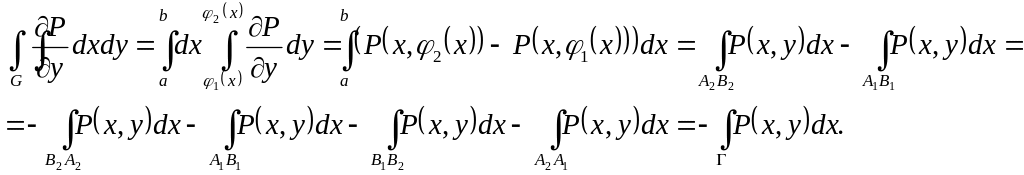
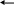
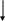
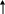
Замечание 5. В силу аддитивности формула Грина справедлива и для областей, которые можно разбить на конечное число элементарных.
Утверждение 11. Замена переменных (двумерный случай).
Если:
,
- диффеоморфизм,
,
,
,
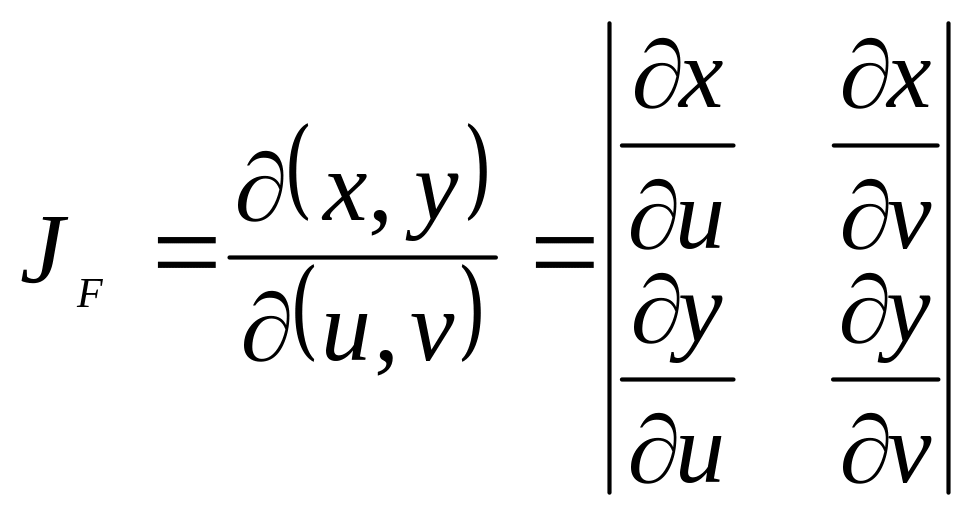- элементарная область:
- положительно ориентированная граница
,
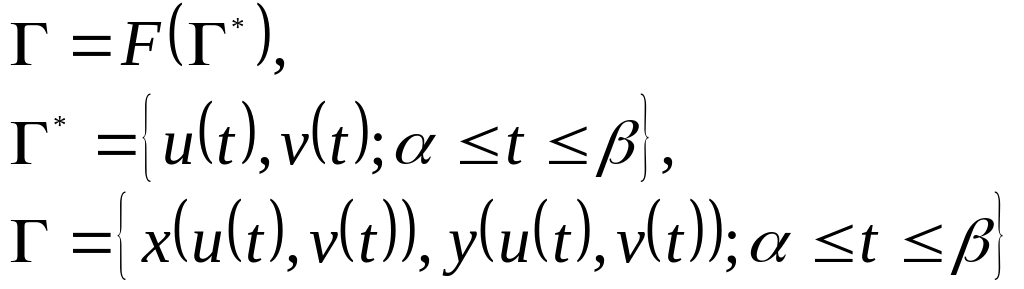
То:
.
Док-во: По нашим предположениям оба интеграла существуют как интегралы от непрерывных функций по измеримым множествам.
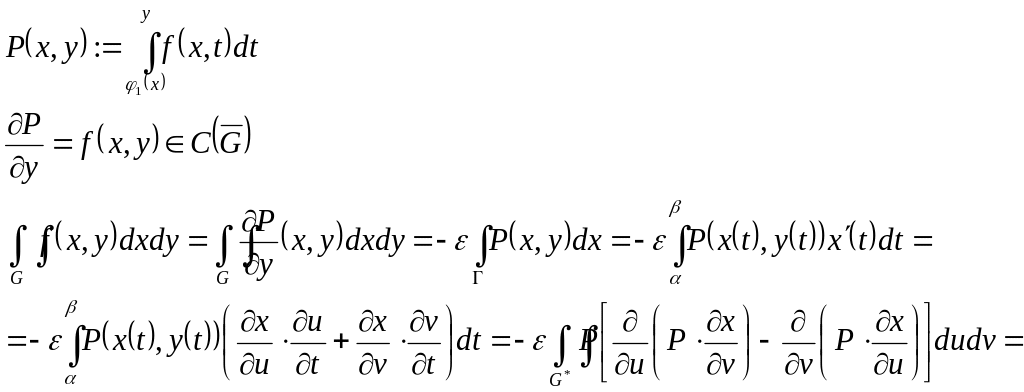
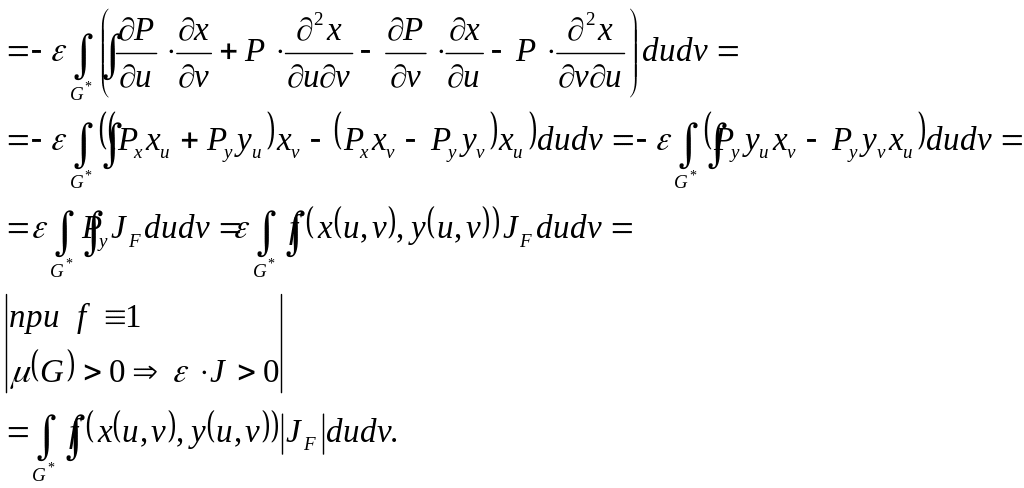
Следствие 11. Если якобиан положительный (отрицательный), то отображение сохраняет (меняет) ориентацию контура.
Лекция 4 Геометрический смысл модуля якобиана отображения
Утверждение 12.
Если:
,
То:
.
Док-во:
Т.о. модуль якобиана отображения – коэффициент изменения площади области.
Утверждение 13. Замена переменных
(
мерный
случай).
Если:
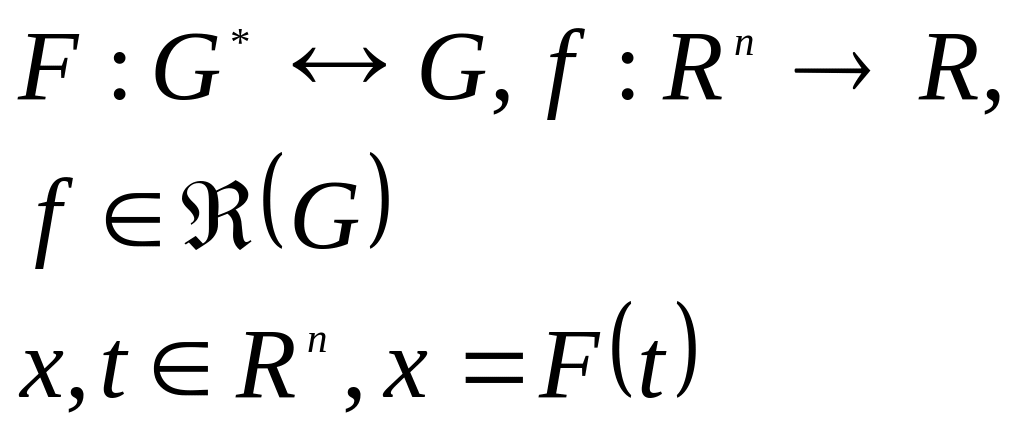
То:
,
.
Пример 1. Полярные координаты.
.
Пример 2. Цилиндрические координаты.
Пример 3. Сферические координаты.
1.3. Приложения кратных интегралов
Везде далее
-измеримо,
Площадь.
Масса.
- плотность
Статический момент.
- статический момент пластины
относительно оси
Центр масс.
Определение 1. Точка
называется центром масс, если материальная
точка, помещённая в
,
с массой, равной массе тела, имеет
одинаковый с телом статический момент.
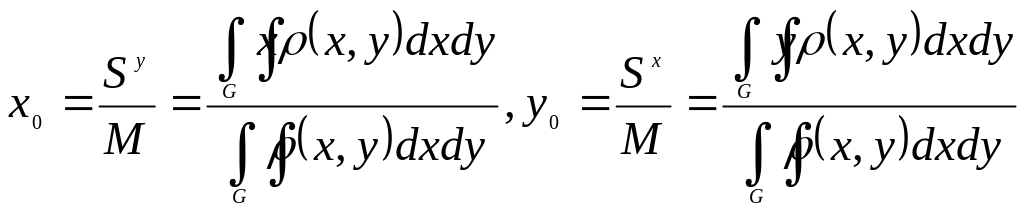
Момент инерции.
- момент инерции пластины
относительно оси
- момент инерции относительно начала
координат.
Лекция 5
1.4. Несобственные кратные интегралы
Определение 1. Будем называть
последовательность множеств
последовательностью, монотонно
исчерпывающей множество
,
если:
,
- открытые в
,
1)
2)
.
Определение 2. Будем называть
несобственным кратным интегралом по
множеству
от функции
если
- последовательность, монотонно
исчерпывающая
,
- измеримы
этот предел существует и конечен.
Замечание 1. Когда мы говорим о
несобственном кратном интеграле по
множеству
,
мы подразумеваем, что
существует собственный интеграл
.
Замечание 2. Данное выше определение более строгое, чем определение несобственного интеграла в одномерном случае.
Теорема 1.
Свойства.
1. Линейность
2. Если:
,
То:
.
3. Аддитивность по множеству.
4. Замена переменных.
Пункты 3,4 расписываются так же, как в обычных интегралах.