
- •Теория множеств, действия над множествами. Конечные, счетные и несчетные множества. Счетность множества рациональных чисел q.
- •Понятие поля, упорядоченного поля. Точная верхняя и нижняя грани ограниченного множества. Необходимое и достаточное условие существования точней верхней грани множества. Примеры.
- •Замечание
- •Доказательство
- •Монотонные последовательности, существование предела у ограниченной монотонно последовательности. Неравенство Бернулли, второй замечательный предел.
- •Часть 1. Пусть ограниченны сверху, т.Е. Такое, что . Тогда, согласно теореме о существовании супремума мы можем утверждать, что .
- •Часть 2. Пусть теперь неограниченна сверху. Это значит, что .
- •Непрерывные функции. Непрерывность простейших элементарных функций. Класс элементарных функций, непрерывность его элементов.
- •12) Предел функции в бесконечности и предел функции, равный бесконечности. Предел функции в бесконечности
- •13) Бесконечно малые и бесконечно большие функции, из связь. Свойства бесконечно малых(конечная сумма, произведение б.М. На ограниченную функцию). Сравнение бм и ббфунций.
- •Производная. Геометрический и механический смысл производной
- •16) Производная сложной функции. Примеры. Производная обратной функции. Вывод производной для арксин, арктг.
- •19)Диффернцирование функции одной переменной. Инвариантность первого дифференциала.
- •20) Старшие производные. Формула Лейбница. Примеры.
- •21) Свойства функций, дифференцируемых на отрезке. Теорема Ферма. Теорема Ролля и ее геометрический смысл. Теорема Лагранжа и ее геометрический смысл. Теорема Коши.
- •22) Правило Лопиталя. Раскрытие неопределенностей.
- •23) Многочлен Тейлора. Формула Тейлора с остаточным членом в форме Лагранжа, Пеано.
- •24) Разложение основных элментарных функций в ряд Маклорена.
- •25) Локальный Экстремум функции одной переменной, необходимые и достаточные условия.
Теория множеств, действия над множествами. Конечные, счетные и несчетные множества. Счетность множества рациональных чисел q.
Множество A – совокупность элементов, объединённых каким-нибудь общим свойством.
Операции над множествами:
- объединение множеств A и B = { x : xили xB}
- пересечение множеств A и B: = { x : xиxB}
- разность множеств A и B: \ B = { x : xи xB }
- симметрическая разность множеств A и B: B = (A \ B)(B \ A)
-
дополнение
множества A
относительно U,
AU:
![]() =
U
\ A
=
U
\ A
Счётное
мно́жество есть бесконечное
множество,
элементы которого возможно
пронумеровать натуральными
числами.
Более формально: множество X является
счётным, если существует биекция ![]() ,
где
,
где ![]() обозначает
множество всех натуральных чисел.
Другими словами, счётное множество —
это множество, равномощное множеству
натуральных чисел.
обозначает
множество всех натуральных чисел.
Другими словами, счётное множество —
это множество, равномощное множеству
натуральных чисел.
Несчётное множество — такое бесконечное множество, которое не является счётным.
Конечное
множество — множество,
количество элементов которого конечно,
то есть, существует неотрицательное целое
число k,
равное количеству элементов этого
множества. В противном случае множество
называется бесконечным.(
Множество ![]() называется конечным,
если оно эквивалентно множеству
называется конечным,
если оно эквивалентно множеству ![]() при
некотором неотрицательном целом
при
некотором неотрицательном целом ![]() .
При этом число
называется
количеством элементов множества
,
что записывается как
.
При этом число
называется
количеством элементов множества
,
что записывается как ![]() .)
.)
Множество Q рациональных чисел счётно. Множество рациональных чисел (чисел вида p/q, где p, q – целые числа, q ≠ 0) можно представить как объединение счётного числа следующих счётных множеств: множества Q1 всех целых чисел n=0, 1, 2, 3,….; множество Q2 всех дробей вида n/2, множество Q3 всех дробей вида n/3,……………., множество Qк всех дробей вида n/к, n=0, 1, 2, 3,…..; следовательно, оно счётно.
Понятие поля, упорядоченного поля. Точная верхняя и нижняя грани ограниченного множества. Необходимое и достаточное условие существования точней верхней грани множества. Примеры.
По́лем называется множество F с
двумя бинарными
операциями + (аддитивная
операция,
или сложение)
и ![]() (мультипликативная
операция,
или умножение),
если оно (вместе с этими операциями)
образует коммутативное ассоциативное кольцо c
единицей
(мультипликативная
операция,
или умножение),
если оно (вместе с этими операциями)
образует коммутативное ассоциативное кольцо c
единицей ![]() ,
все ненулевые элементы которого обратимы.
,
все ненулевые элементы которого обратимы.
Иными
словами, множество F с
двумя бинарными операциями + (сложение)
и
(умножение)
называется полем,
если оно образует коммутативную
группу(Абелева или коммутативная
группа есть группа,
в которой групповая
операция является коммутативной;
то есть группа (G,
* ) абелева
если a * b = b * a для
любых двух элементов ![]() ). По
сложению, все его ненулевые элементы
образуют коммутативную группу по
умножению, и выполняется
свойство дистрибутивности.(
). По
сложению, все его ненулевые элементы
образуют коммутативную группу по
умножению, и выполняется
свойство дистрибутивности.(![]() )
)
Примеры множеств, являющихся полями
 — рациональные
числа,
— рациональные
числа, — вещественные
числа,
— вещественные
числа, — комплексные
числа,
— комплексные
числа,
Свойства поля
1.Характеристика поля всегда 0 или простое число.(Просто́е число́ — это натуральное число, имеющее ровно два различных натуральных делителя: единицу и самого себя.)
2.Поле характеристики 0 содержит подполе, изоморфное полю рациональных чисел .
3.Поле простой характеристики p содержит подполе, изоморфное(Пусть даны два множества с определённой структурой (группы, кольца, линейные пространства и т. п.). Биекция между ними называется изоморфизмом, если она сохраняет эту структуру. Если между такими множествами существует изоморфизм, то они называются изоморфными. Изоморфизм всегда задаёт отношение эквивалентности на классе таких множеств со структурой.Объекты, между которыми существует изоморфизм, являются в определённом смысле «одинаково устроенными», они называются изоморфными.) полю вычетов .
4.Количество элементов в конечном поле всегда равно pn — степени простого числа.
5.При этом для любого числа вида pn существует единственное (с точностью до изоморфизма) поле из pn элементов, обычно обозначаемое .
6.Любой ненулевой гомоморфизм( Это отображение алгебраической системы А, сохраняющее основные операции и основные соотношения.
Например,
рассмотрим группы ![]() ,
, ![]() .
Отображение
.
Отображение ![]() называется
гомоморфизмом групп
называется
гомоморфизмом групп ![]() и
и ![]() ,
если оно одну групповую операцию
переводит в другую:
,
если оно одну групповую операцию
переводит в другую: ![]() .)
.)
полей является вложением(Вложение в математике — это специального вида отображение одного экземпляра некоторой математической структуры во второй экземпляр такого же типа.)
7.В поле нет делителей нуля.
Упорядоченное
поле — алгебраическое
поле,
для всех элементов которого
определён линейный
порядок(Линейно
упорядоченное множество или цепь ― частично
упорядоченное множество,
в котором для любых двух элементов a и b имеет
место ![]() или
или ![]() ),согласованный с операциями поля.
Наиболее практически важными примерами
являются поля рациональных и вещественных
чисел.
),согласованный с операциями поля.
Наиболее практически важными примерами
являются поля рациональных и вещественных
чисел.
Пусть F — алгебраическое
поле и
для его элементов определён линейный
порядок,
то есть задано отношение ![]() (меньше
или равно) со следующими свойствами:
(меньше
или равно) со следующими свойствами:
Рефлексивность:
 .
.Транзитивность: если
 и
и 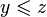 ,
то
,
то  .
.Антисимметричность: если и
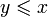 ,
то
,
то 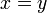 .
.Линейность: все элементы F сравнимы между собой, то есть либо
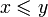 ,
либо
.
,
либо
.Согласованность со сложением: если , то для любого z:
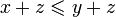 .
.Согласованность с умножением: если
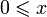 и
и 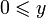 ,
то
,
то 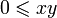 .
.
Некоторые свойства
Всякий элемент упорядоченного поля относится к одной и только одной из трёх категорий: положительные числа, отрицательные числа, нуль. Если x положителен, то − x отрицателен, и наоборот.
В любом упорядоченном поле 1 > 0 и квадрат любого ненулевого элемента положителен.
Однотипные неравенства можно складывать:
Если
и ![]() ,
то
,
то ![]() .
.
Неравенства можно умножать на положительные элементы:
Если
и ![]() ,
то
,
то ![]() .
.
Примеры
Рациональные числа
Вещественные числа
Вещественные алгебраические числа
Поле вещественных рациональных функций:
 ,
где
,
где 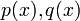 — многочлены,
— многочлены,  .
Упорядочим его следующим образом.
.
Упорядочим его следующим образом.Вещественные константы (как многочлены нулевого порядка) упорядочены традиционным образом.
Точная верняя и нижняя грани огр. Мн-ва
Точной (наименьшей) верхней гранью (границей), или супре́мумом (лат. supremum — самый высокий) подмножества X упорядоченного множества (или класса) M, называется наименьший элемент M, который равен или больше всех элементов множества X. Другими словами, супремум — это наименьшая из всех верхних граней. Обозначается sup X.
Более формально:
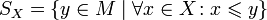 —
множество верхних
граней X,
то есть элементов M,
равных или больших всех элементов X
—
множество верхних
граней X,
то есть элементов M,
равных или больших всех элементов X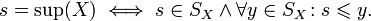
Точной (наибольшей) нижней гранью (границей), или и́нфимумом (лат. infimum — самый низкий) подмножества X упорядоченного множества (или класса) M, называется наибольший элемент M, который равен или меньше всех элементов множества X. Другими словами, инфимум — это наибольшая из всех нижних граней. Обозначается inf X.
Замечание
Эти определения ничего не говорят о том, принадлежит ли sup X и inf X множеству X или нет. В случае
 ,
говорят, что s является максимумом X.
В случае
,
говорят, что s является максимумом X.
В случае 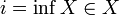 ,
говорят, что i является минимумом X.
,
говорят, что i является минимумом X.
Примеры
На множестве всех рациональных чисел, больших пяти, не существует минимума, однако существует инфимум. inf такого множества равен пяти. Инфимум не является минимумом, так как пять не принадлежит этому множеству. Если же определить множество всех натуральных чисел, больших пяти, то у такого множества есть минимум и он равен шести. Вообще говоря, у любого непустого подмножества множества натуральных чисел существует минимум[1].
Для множества
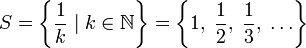
sup S = 1; inf S = 0.
Множество положительных рациональных чисел
 не
имеет точной верхней грани в
,
точная нижняя грань
не
имеет точной верхней грани в
,
точная нижняя грань 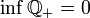 .
.Множество
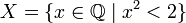 рациональных
чисел, квадрат которых меньше двух, не
имеет точных верхней и нижней граней
в
,
но если его рассматривать как подмножество
множества действительных
чисел,
то
рациональных
чисел, квадрат которых меньше двух, не
имеет точных верхней и нижней граней
в
,
но если его рассматривать как подмножество
множества действительных
чисел,
то
![]() и
и ![]() .
.
Теорема :Непустое множество, ограниченное сверху, имеет верхнюю грань, ограниченное снизу — нижнюю грань. То есть существуют a и b такие, что
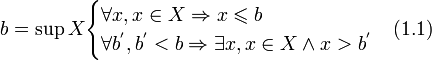
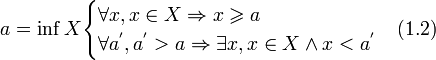
Доказательство
Для
множества ограниченного сверху. Пусть ![]() -
мажоранта множества
,
представленная в виде бесконечной
десятичной дроби.
Множество
непусто.
Запишем все числа
-
мажоранта множества
,
представленная в виде бесконечной
десятичной дроби.
Множество
непусто.
Запишем все числа ![]() из
в
виде нормальных десятичных дробей,
из
в
виде нормальных десятичных дробей,
![]() .
.
Множество ![]() непусто
и ограниченно сверху числом
непусто
и ограниченно сверху числом ![]() ,
поэтому существует
,
поэтому существует ![]() .
.
Множество ![]() десятичных
чисел вида
десятичных
чисел вида ![]() таких,
что среди элементов
есть
число, представление которого в виде
бесконечной десятичной дроби начинается
с выражения
,
непусто и состоит не более чем из десяти
элементов, поэтому существует
таких,
что среди элементов
есть
число, представление которого в виде
бесконечной десятичной дроби начинается
с выражения
,
непусто и состоит не более чем из десяти
элементов, поэтому существует ![]() .
.
Допустим,
что для некоторого номера ![]() построено
десятичное число
построено
десятичное число ![]() такое,
что
такое,
что
существует элемент
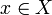 ,
представление которого в виде бесконечной
десятичной дроби начинается с выражения
,
представление которого в виде бесконечной
десятичной дроби начинается с выражения
если x - элемент с представлением
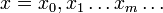 ,
то
,
то
![]() .
.
Обозначим ![]() множество
десятичных чисел вида
множество
десятичных чисел вида ![]() ,
которые служат начальными выражениями
для элементов множества
.
По определению числа
на
основании свойства 1 множество
непусто.
Оно конечно, поэтому существует число
,
которые служат начальными выражениями
для элементов множества
.
По определению числа
на
основании свойства 1 множество
непусто.
Оно конечно, поэтому существует число ![]() ,
обладающее свойствами 1-2 с
заменой
на
,
обладающее свойствами 1-2 с
заменой
на ![]() ,
причем появление
,
причем появление ![]() -ого
знака после запятой не влияет на величины
предшествующих знаков.
-ого
знака после запятой не влияет на величины
предшествующих знаков.
На
основании принципа индукции для
любого
оказывается
определенной цифра ![]() и
поэтому однозначно определяется
бесконечная десятичная дробь
и
поэтому однозначно определяется
бесконечная десятичная дробь
![]()
Возьмем
произвольное число ![]() .
По построению числа b для
любого номера n выполняется
.
По построению числа b для
любого номера n выполняется ![]() и
поэтому
и
поэтому ![]() .
Следовательно, выполнена верхняя строчка
в правой части соотношения 1.1 (смотри
формулировку). Следовательно, b =
sup X.
.
Следовательно, выполнена верхняя строчка
в правой части соотношения 1.1 (смотри
формулировку). Следовательно, b =
sup X.
Для множества , ограниченного снизу, рассуждения проводятся аналогично.
Свойства
По теореме о гранях для любого ограниченного сверху подмножества , существует sup .
По теореме о гранях для любого ограниченного снизу подмножества , существует inf .
Вещественное число s является sup X тогда и только тогда, когда
s есть верхняя грань X то есть для всех элементов ,
 .
.для любого ε > 0 найдётся , такой, что x + ε > s (то есть к s можно сколь угодно «близко подобраться» из множества X)
Аналогичное утверждение верно для точной нижней грани.
Существование точной верхней грани множества
????
Числовые последовательности, предел последовательности, сходящиеся и расходящиеся последовательности. Примеры. Свойства сходящихся последовательностей: единственность предела, ограниченность, сохранение знака. Теоремы о пределе суммы(разности), произведение частного двух последовательностей. Теорема о пределе промежуточной последовательности.
Пусть
множество X —
это либо множество вещественных чисел
,
либо множество комплексных чисел
.
Тогда последовательность ![]() элементов
множества X называется
числовой
последовательностью.
элементов
множества X называется
числовой
последовательностью.
Примеры
Функция
 является
бесконечной последовательностью целых
чисел.
Начальные отрезки этой последовательности
имеют вид
является
бесконечной последовательностью целых
чисел.
Начальные отрезки этой последовательности
имеют вид  .
.Функция
 является
бесконечной последовательностью рациональных
чисел.
Начальные отрезки этой последовательности
имеют вид
является
бесконечной последовательностью рациональных
чисел.
Начальные отрезки этой последовательности
имеют вид  .
.Функция, сопоставляющая каждому натуральному числу
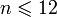 одно
из слов «январь», «февраль», «март»,
«апрель», «май», «июнь», «июль», «август»,
«сентябрь», «октябрь», «ноябрь»,
«декабрь» (в порядке их следования
здесь) представляет собой последовательность
вида
одно
из слов «январь», «февраль», «март»,
«апрель», «май», «июнь», «июль», «август»,
«сентябрь», «октябрь», «ноябрь»,
«декабрь» (в порядке их следования
здесь) представляет собой последовательность
вида  .
В частности, пятым членом x5 этой
последовательности является слово
«май».
.
В частности, пятым членом x5 этой
последовательности является слово
«май».
Число ![]() называется пределом
числовой последовательности
называется пределом
числовой последовательности ![]() ,
если последовательность
,
если последовательность ![]() является
бесконечно малой, т. е. все её элементы,
начиная с некоторого, по модулю меньше
любого заранее взятого положительного
числа.
является
бесконечно малой, т. е. все её элементы,
начиная с некоторого, по модулю меньше
любого заранее взятого положительного
числа.
![]()
В
случае, если у числовой последовательности
существует предел в виде вещественного
числа ![]() ,
её называют сходящейся к
этому числу. В противном случае,
последовательность называют расходящейся.
Если к тому же она неограниченна, то её
предел полагают равным бесконечности.
,
её называют сходящейся к
этому числу. В противном случае,
последовательность называют расходящейся.
Если к тому же она неограниченна, то её
предел полагают равным бесконечности.
![]()
Кроме того, если все элементы неограниченной последовательности, начиная с некоторого номера, имеют положительный знак, то говорят, что предел такой последовательности равен плюс бесконечности.
![]()
Если же элементы неограниченной последовательности, начиная с некоторого номера, имеют отрицательный знак, то говорят, что предел такой последовательности равен минус бесконечности.
![]()
Частичный предел последовательности — это предел одной изеё подпоследовательностей.
Верхний предел последовательности — это наибольшая из её предельных точек.
Нижний предел последовательности — это наименьшая из её предельных точек.
Арифметические свойства
Оператор взятия предела числовой последовательности является линейным, т. е. проявляет два свойства линейных отображений.
Аддитивность. Предел суммы числовых последовательностей есть сумма их пределов, если каждый из них существует.
![]()
Однородность. Константу можно выносить из-под знака предела.
![]()
Предел произведения числовых последовательностей факторизуется на произведение пределов, если каждый из них существует.
![]()
Предел отношения числовых последовательностей есть отношение их пределов, если эти пределы существуют и последовательность-делитель не является бесконечно малой.
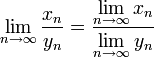
Свойства сохранения порядка
Если все элементы сходящейся последовательности, начиная с некоторого номера, не превышают некоторого числа, то и предел этой последовательности также не превышает этого числа.
![]()
Если некоторое число не превышает все элементы сходящейся последовательности, начиная с некоторого номера, то оно также не превышает и предела этой последовательности.
![]()
Если некоторое число строго превышает все элементы сходящейся последовательности, начиная с некоторого номера, то предел этой последовательности не превышает этого числа.
![]()
Если все элементы сходящейся последовательности, начиная с некоторого номера, строго превышают некоторое число, то это число не превышает предела этой последовательности.
![]()
Если, начиная с некоторого номера, все элементы одной сходящейся последовательности не превышают соответствующих элементов другой сходящейся последовательности, то и предел первой последовательности не превышает предела второй.
![]()
Для числовых последовательностей справедлива теорема о двух милиционерах (принцип двустороннего ограничения).
![]()
Другие свойства
Сходящаяся числовая последовательность имеет только один предел.
![]()
Замкнутость. Если все элементы сходящейся числовой последовательности лежат на некотором отрезке, то на этом же отрезке лежит и её предел.
![]()
Предел последовательности из одного и того же числа равен этому числу.
![]()
Замена или удаление конечного числа элементов в сходящейся числовой последовательности не влияет на её предел.
У возрастающей ограниченной сверху последовательности есть предел. То же верно для убывающей ограниченной снизу последовательности.
Имеет место теорема Штольца.
Если у последовательности xn существует предел, то последовательность средних арифметических
 имеет
тот же предел (следствие из теоремы
Штольца).
имеет
тот же предел (следствие из теоремы
Штольца).
Если у последовательности чисел существует предел , и если задана функция
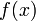 ,
определенная для каждого
,
определенная для каждого 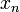 и
непрерывная в точке
,
то
и
непрерывная в точке
,
то
![]()
Сходящиеся и расходящиеся последовательности
Определение. Последовательность {xn} называется сходящейся, если существует такое вещественное число а, что последовательность {xn−a}является бесконечно малой. Если последовательность {xn→a} является сходящейся и имеет своим пределом число a, то символически это записывают так:limn→∞xn=a или xn→a при n→∞ Определение. Последовательность {xn} называется сходящейся, если существует такое вещественное число a, что для любого положительного вещественного числа ε найдется номер N(ε) такой, что при всехn>Nэлементы xn этой последовательности удовлетворяют неравенству ∣xn−a∣<ε При этом число a называется пределом последовательности.
Свойства
Теорема 1. Сходящаяся последовательность имеет только один предел. Доказательство. Предположим, что два вещественных числа а и b являются пределами сходящейся последовательности {xn}. xn=a+an и xn=b+bn, где {an} и {bn} - некоторые бесконечно малые последовательности. Получим an−bn=b−a. Последовательность {an−bn} является бесконечно малой, а в силу равенства an−bn=b−a все элементы этой бесконечно малой последовательности равны одному и тому же вещественному числуb−a. Число b−a равно нулю, т. е. b=a. Теорема доказана.
Теорема 2. Всякая сходящаяся последовательность является ограниченной.
Доказательство. Пусть {xn} - сходящаяся последовательность и a ее предел. Фиксируем некоторое положительное число ε и по нему номер N такой, что ∣xn−a∣<ε при n≥N или, a−ε<xn<a+εпри n≥N. Обозначим через A наибольшее из следующих (N+1) чисел: ∣a−ε∣,∣a+ε∣,∣ ∣ x1∣ ∣ ,∣ ∣ x2∣ ∣ ,...,∣ ∣ хN−1∣ ∣ . Тогда, очевидно, ∣xn∣≤A для всех номеров n, а это и доказывает ограниченность последовательности {xn}. Теорема доказана.
Следствие 1. Не всякая ограниченная последовательность является сходящейся. Так, например, посл. 0,1,0,1,...,0,1, ... является ограниченной, но не является сходящейся. В самом деле, обозначим n-й член этой последовательности символом xn и предположим, что эта последовательность сходится к некоторому пределу a. Но тогда каждая из последовательностей {xn+1−a} и {xn−a} являлась бы бесконечно малой. Стало быть, являлась бы бесконечно малой и разность этих последовательностей {xn+1−xn} а этого быть не может в силу того, что ∣ ∣ xn+1−xn∣ ∣ =1 для всех номеров n. Последовательность {an} называется бесконечно малой, если для любого положительного вещественного числа ε найдется номер N(ε) такой, что при всех n>Nэлемент an последовательности удовлетворяет неравенству ∣an∣<ε.
Теорема 3. Сумма сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен сумме пределов последовательностей {xn} и {yn}. Доказательство. Предположим, что последовательности {xn} и {yn} сходятся к пределам а и b соответственно. Тогда в силу того что xn=a+an будут справедливы соотношения xn=a+an,yn=b+bn, (6), в которых anи bn представляют собой элементы некоторых бесконечно малых последовательностей {an}и {bn}. Из (6) вытекает, что(xn+yn)−(a−b)=an+bn. (7) Т.к. сумма {an+bn} двух бесконечно малых последовательностей {an} и {bn} представляет собой бесконечно малую последовательность, то из соотношения (7) вытекает в силу определения, что последовательность {xn+yn} сходится и вещественное число a+b является ее пределом. Теорема доказана.
Теорема 4. Разность сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен разности пределов последовательностей {xn} и {yn} Доказательство этой теоремы аналогично доказательству Теоремы 3, только вместо соотношения (7) мы получим соотношение (xn−yn)−(a−b)=an−bn.
Теорема 5. Произведение сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен произведению пределов последовательностей {xn} и {yn}. Доказательство. Предположим, что последовательности {xn} и {yn}сходятся к пределам a и bсоответственно. Тогда для элементов этих последовательностей справедливы (6), перемножая которые, мы получим xn·yn=a·b+abn+ban+an·bn или, xnyn−a·b=abn+ban+an·bn (8)
Теорема о пределе промежуточной (зажатой) функции
Пусть функции f(x) и g(x) таковы, что существует lim (x->a) f(x) = lim(x->a) g(x) = A (A<>oo) и пусть существует проколотая дельта-окрестность а, в которой выполняется неравенство f(x)<=h(x)<=g(x), для любого х существует проколотая дельта-окрестность точки а. Тогда существует lim (x->a) h(x)=a
Система вложенных стягивающихся отрезков. Теорема Кантора. Несчетность R. Теорема Больцано-Вейерштрасса о выделении из ограниченной последовательности сходящейся подпоследовательности. Подпоследовательности, верхний и нижний пределы последовательности. Примеры. Фундаментальные последовательности, Критерий Коши. Примеры.
Формулировка
Для всякой системы вложенных отрезков
![]()
существует хотя бы одна точка c, принадлежащая всем отрезкам данной системы.
Если, кроме того, длина отрезков системы стремится к нулю:
![]()
то c — единственная общая точка всех отрезков данной системы.
