3 4. Сложные схемы параллельного колебательного контура
В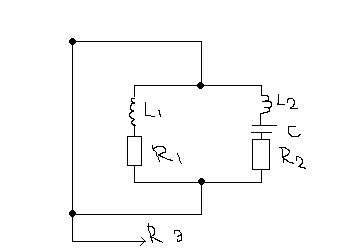
торой
вид
Т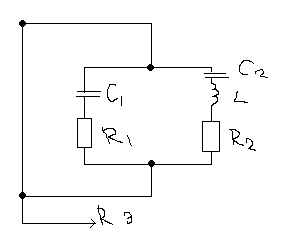
ретий
вид
Согласование сопротивления источника и нагрузки используют контур 2-го и 3-го вида.
35. Двухэлементные и трехэлементные реактивные двухполюсники.
Реактивными двухполюсниками называются колебательные контуры без потерь по отношению их к входным зажимам.
Частотные хар-ки
Zвх (jw) ; Xвх (w)
Д
вухэлементные
( послед. и параллельные)
X
вх
= wL
– 1/wC
Xвх = Ро^ /wL-(1/wC)
Т
рехэлементные
Zвх = jwLo*(Wo3^ - W^/Wo2^ - W^)
Любой двухполюсник без потерь может быть заменен эквивалентной схемой одного из классов двухполюсников, которые называются каноническими.
Эквив. Двухполюсник – когда частотные хар-ки на всех частотах при соответ. выборе параметров совпадает.
36. Канонич. Схемы реакт. Двухполюсников.
37. Связные колебательные контуры. Схемы с автотрансформаторной, трансформаторной и емкостной связью. Коэффициент связи.
Сист. связных колебательных контуров представляет собой цепи каждое звено которой является колебательным контуром .
Частотные характеристики сущ. отличаются от прямоугольных. В общем виде представляют в виде цепочечной схемы.
А
)
Б
)
Взаимные сопротивления называются сопротивлениями связи. В цепи “а” индуктивный характер, в “б” емкостный.
1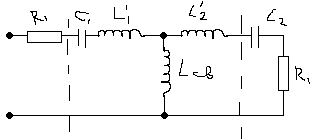
)Автотрансформаторная
2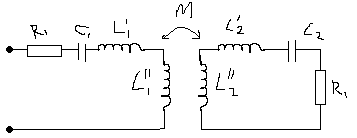
)Трансформаторная
3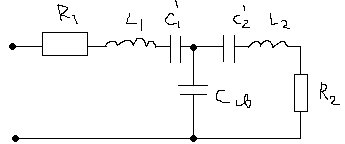
)Емкостной
Контур подключенный к источнику назыв. первичным, а связный с ним 2-ой контур – вторичным
К = K21 * K12 - Коэффициент связи
K21 – коэффициент передачи напряжения из первого во второй. K12 - наоборот.
Для 1) K = Xсв / (L1 * L2)
Для 2) K = (C1-C2)/Cсв
Для 3) K = M/ (L1+L2)
3 8. Входное сопротивление системы связных колебательных контуров.
И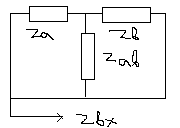
ли
в общем виде
Z1 = Za + Z св
Za = Z1 – Zсв Zвх = Za = ZвZсв / Zв+ Zсв =
= Z1 – Zсв^ / Z где Z = Zв +Zсв
-
Zсв
/ Z
= Zвн
– полное вносимое сопротивление
Zвх= Z1 + Zвн
39. Первичный и вторичные токи в системе связных колебательных контуров.
Первичный ток
. . . .
I = E / Z вх = E /Z1 + Zвн = E / (R1+Rвн) +j(X1 + Xвн)
Активное (Rвн) и реактивное (Xвн) составляющие существенно зависят от реактивной составляющей X2 которая определяется частотой индуктивности, емкостью.
X2= L2 – 1 / C2
Вторичный ток
. . .
I2*(Zв + Z св) – I1Zсв = 0 I2 = I1 *Zсв/ Z
Z = Zв + Zсв
. .
I2 = Zсв E / Z1 Zвых = I’1
40. Настройка системы связных колебательных контуров. Частный и основной резонанс.
Настройка – процесс получить максимум тока(вторичного) при неизменном значение входной Sin-ой ЭДС на заданной частоте.
Частный резонанс
I2= Xсв E / Z2(Z1+(Xсв^/Z^ *R) т.к. Zвх=R1+Rвн
I2 = Xсв E / Z1(R2+(Xсв^ / Z^) *R) т.к.
Zвых = R+Rвн’
Основной резонанс
Называется резонанс при котором оба контура, будучи уединенными настраиваются каждый в резонанс, а сопротивление связи имеет произвольное неизменное значение. При основном резонансе выполняется условие обоих частных резонансов. Значение тока при этом могут быть получены из любой формулы для I2.
X1 = X2 = 0
Xсв =const ; Z1=R1 ; Z2=R2 ; Zсв=jXсв
Iгр = jXсв E / R1R2 = Rсв ^
41. Сложный резонанс в системе связных колебательных контуров.
Резонанс системы, при котором выполнено одно из условий одного из частных резонансов и подобрана наиболее выгодная связь называется сложным резонансом.
42. Энергетические состояния в системе связных колебательных контуров.
Эффективность передачи энергии характеризуется КПД системы связных контуров
к = Rвн / R1 + Rвн = 1 / 1+(R1/ Rв) (1)
R1 – сопр. того источника энергии , кот. этот контур питает.
К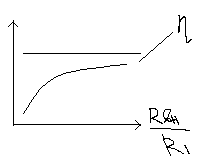
ПД()
растет в зависимости от отношения (1).
Это можно представить в виде графика
43. Зависимость полосы пропускания системы связных колебательных контуров от параметра связи.
Частотные характеристики позволяют судить о полосе пропускания и равномерности амплитуды тока или напряжения в полосе пропускания.
I2 = I1Xсв / Z2
I1 – определяется входным напряжением Zвх.
Zвх = (R1 + Rвн)^+(X1 + Xвн)^
44. Частотные хар-ки перв. И втор. Тока системы связан. Колебательных контуров.
45. Элементы контуров при высоких частотах. ЭКВИВАЛЕНТНЫЕ СХЕМЫ.