4.4 Оценка погрешности интерполяционной формулы Лагранжа
(8)
Заменяем в вычислениях значение функции значением интерполяционного многочлена в формуле (8), мы допускаем тем самым погрешность.
Обозначим разность
-
остаточный член формулы Лагранжа. Он и
дает погрешность метода.
Теорема: если
функция
имеет на
непрерывную производную до (n+1)
порядка
,
то остаточный член
можно представить в ви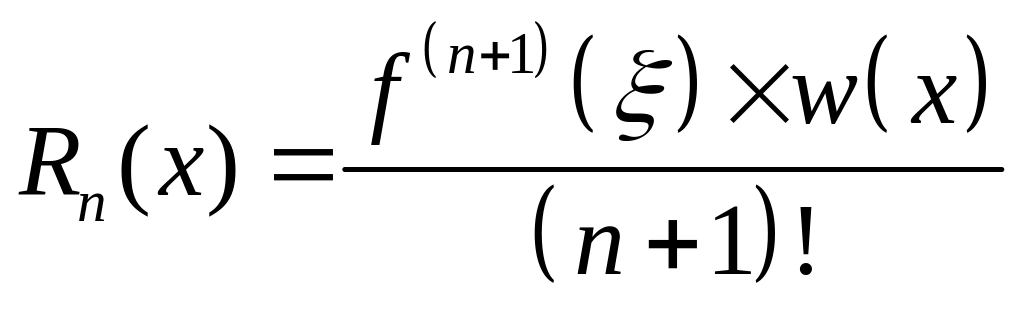де
,
где
.
Если будет известно,
что
,
то получим оценку погрешности.
(9)
Формула (9) дает погрешность метода
Пример: С какой
точностью можно вычислить
,
с помощью интерполяционной формулы
Лагранжа построенный для функции
,используя
3 узла интерполяции.
n+1=3,
n=2
– степень многочлена
За
можно принять
на отрезке
,
на отрезке
4.5 Табличные разности (конечные разности)
Пусть функция
задана в равноотстоящих узлах
интерполяции. Назовем узлы интерполирования
равноотстоящими, если они пронумерованы
в порядке возрастания и расстояние
между соседними узлами одинаковое
равное h
,
то есть задается таблица с постоянным
шагом h.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|||||
|
|
||||
|
|||||
|
|||||
|
|
|
|||
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|||||
|
|
||||
Разности между соседними табличными значениями функции называют табличными разностями 1-го порядка (первые табличные разности).
- единственное
значение
Пример:
Табличные разности любого порядка могут быть выражены через значения функции:
4.6 Интерполяционный многочлен Ньютона
Пусть функция
задана таблицей с постоянным шагом h,
то есть
Будем искать интерполяционный многочлен в виде:
(10)
Неизвестный
коэффициент найдем из (*)
При
Полагая, что при
Полагая, что при
Проведя аналогичные рассуждения, получаем:
Подставив полученные коэффициенты в ( 10 ), будем иметь
(11)
Многочлен (11) и есть интерполяционный многочлен Ньютона.
На практике многочлен Ньютона применяют в несколько ином виде.
Если обозначим
,
то
Многочлен (11) примет вид
(12)
Многочлен (12) и называют первый интерполяционный многочлен Ньютона.
В выражение
многочлена входят табличные разности
Поэтому этот многочлен используют для интерполирования в начале таблицы, когда t мало по абсолютной величине
Замечание: если
требуется вычислить значение функции
для аргумента
,
то за
выбирают ближайшее, причем меньшее
табличное значение аргумента.
Пример:
|
|
1.5 |
3.7 |
1.6 |
3.9 |
1.7 |
4.1 |
1.8 |
4.5 |
1.9 |
5.0 |
|
|
Приближенное равенство
(13)
называют интерполяционной формулой Ньютона.