§4 Интерполирование

4.1 Постановка задачи

Пусть в (n+1) точках задана непрерывная функция со своими значениями , то есть фактически задана таблица

(1)

Требуется найти значение функции f для аргумента , но не совпадающего с табличным

Если аналитическое выражение функции неизвестно или очень сложное, то часто прибегают к замене функции на , которая в некотором смысле близка к функции и аналитическое выражение которой будет известно.

Записывают , где - приближающая функция.

Существуют различные способы построения приближающей функции. Это зависит от выбора критерия близости.

Классическое построение приближающей функции основывается на требовании строгом совпадения значений функции и в заданных точках, то есть ;

Нахождение функции, удовлетворяющей этим условиям, называется интерполированием или интерполяцией.

- интерполирующая функция;

- интерполируемая функция;

заданные точки - узлы интерполяции.

Будем искать интерполирующую функцию в виде многочлена степени не выше n, который в заданных точках принимает такие же значения, что и заданная функция .

( * ) – условие интерполирования, . Многочлен называется интерполяционным многочленом, само интерполирование - параболическим.

Таблица 1 задает систему точек геометрический смысл интерполяции заключается в том, что график функции заменяется параболой n –го порядка, являющийся графиком и проходящей через заданные точки , то есть график функции и имеют (n+1) общую точку.

4.2 Существование и единственность интерполяционного многочлена

Интерполяционный многочлен можно записать по убывающим степеням.

(2)

Неизвестные коэффициенты многочлена будем искать из условия ( * ).

Получим систему из (n+1) уравнения с неизвестными

(3)

(3) – линейная неоднородная система.

Запишем определитель системы , где - определитель Вандермонда,

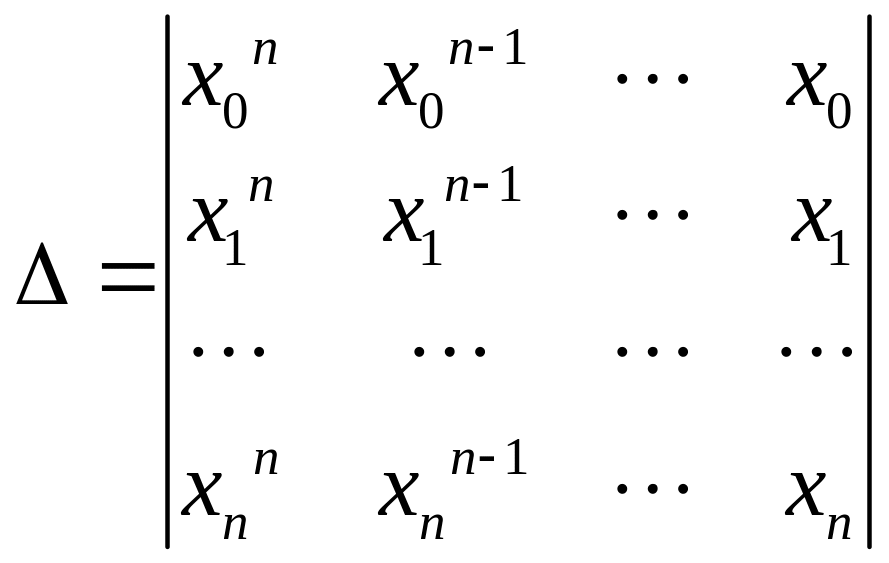
Так как узлы интерполирования различны, то определитель система (3) имеет единственное решение, то есть коэффициенты многочлена (2) существуют и определяются единственным образом.

Замечание: решая системы с (n+1) неизвестными, то есть имея (n+1) узел интерполяции, мы получаем многочлен степени не выше n.

Такой способ отыскания коэффициентов многочлена связан с решением системы, увеличение количества узлов интерполяции приводит к большим трудоемким вычислениям. Другой способ отыскания коэффициентов был предложен Лагранжом.

4.3 интерполяционный многочлен Лагранжа

Пусть функция задана таблицей 1, построим интерполяционный многочлен , который удовлетворял бы условию (*). Будем искать в виде

(4),

где - многочлен степени не выше n и удовлетворяет следующему условию:

(**)

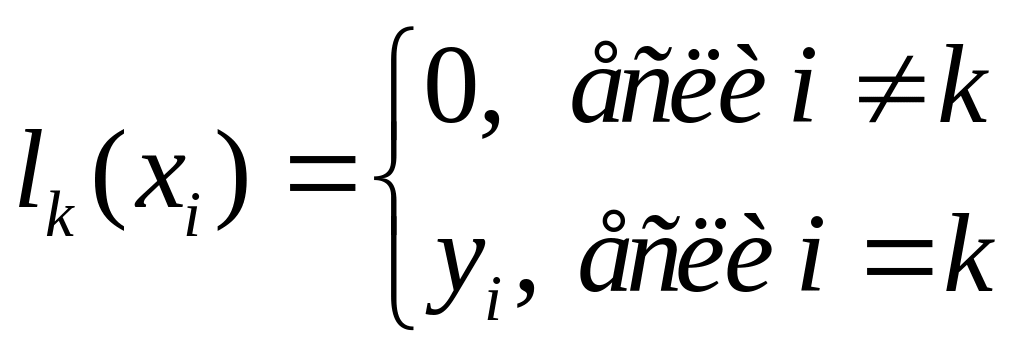Из условия (**) следует, что все узлы, кроме одного, а именно являются нулями многочлена .

(5)

А при ; ,

тогда

Подставляя в (5) получаем

Так как , то окончательно получим

(6)

Многочлен (6) и есть многочлен Лагранжа.

Многочлен (6) можно записать и в более краткой форме.

Обозначим - многочлен (n+1) степени.

Производная от точки имеет вид:

(7)

Многочлен (7) и есть краткая запись многочлена Лагранжа.

Приближенное равенство

(8)

называется интерполяционная форма Лагранжа.

Пример: построить интерполяционный многочлен Лагранжа для функции заданной таблицей.

	0	0.5	1	2
	1	2	4	3

n +1=4 – количество узлов;

n=3 - степень многочлена.