33.Дисперсия непрерывной св, ее свойства. Стандартное отклонение.

D(X) = M([X-M(X) )=M( =M( M(

Свойства:

Свойства дисперсии:

4. D(X)

5. X = const, то D(X) = 0 ; D(X) = M ((X-M(X)

X = C = const , то D(C) = M ((C-C

6. Дисперсия от суммы случайных величин. Пусть X и Y – случайные независимые величины. Тогда D(X+Y) = D(X)+D(Y)

D(X+Y) = M ((X+Y ) – (M(X+Y) = M ( =(M(

.Нормальный закон распределения вероятностей. Плотность вероятности, математическое ожидание, дисперсия, стандартное отклонение.

N(a,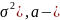 вещественная величина, а

X= N(a,

F(x) = P(X<x) =

f(x)=

M(X)=

D(X) =

P(|X-a|,3

Случайные величины, у которых распределение вероятностей – кусочно гладкая функция

F(x)

F(a+0)>F(a-0)

M(X) =

Нарисовать

Нормированным нормальным распределением называется нормальное распределение с параметрами

.

.

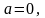
- Функция Лапласа.

35.Вероятность попадания нормально распределенной св в заданный интервал. Правило трех сигм, ее численная реализация.

X F(x) = P(X>x) =

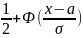
P(X<x) = 1-P(X

F(|X –a | <

Правило трех сигм. Используя формулу: , вычислим для случая .

Правило трех сигм: Если случайная величина имеет нормальное распределение, то абсолютная величина ее отклонения от M(X) не превосходит утроенного среднего квадратического отклонения.

Численная реализация правила трех сигм

σ =

ε = 3 σ

P(| X-M(X) | ≤ 3 σ) ≥ 1 - = 1 - = = 0, 8888

36.Показательное распределение. Плотность, функция распределения, математическое ожидание и дисперсия. Численная реализация правила трех сигм.

E(x); f(x) =

F(x) =

Нарисовать

F(x) =

M(X) =

M

M(

D(X) = M(

Численная реализация правила трех сигм

σ =

ε = 3 σ

P(| X-M(X) | ≤ 3 σ) ≥ 1 - = 1 - = = 0, 8888

37.Равномерное распределение. Плотность, функция распределения, математическое ожидание и дисперсия.

R(a,b) , (a< b)

f(x) =

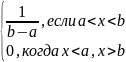
Нарисовать

Площадь равна 1

F(x) =

Нарисовать

M(X) = = =

M(

D(X) =

38.Закон больших чисел. Неравенства Чебышева и Маркова и следствия из них.

{

P( |

Неравенство Чебышева.

Неравенство Чебышева справедливо для ДСВ и НСВ.

Докажем для ДСВ:

Пусть дана ДСВ Х и ее закон распределения.

Теорема: Вероятность абсолютного отклонения случайной величины от M(X) на число не превосходящее  не меньше разности 1- ( D(X) / ²)

P( x – M(X)  <  )  (1 - ( D(X) / ²) )

Доказательство: События { x – M(X)  <  } и { x – M(X)    } противоположны. Тогда вероятность первого события:

P( x – M(X)  <  ) = 1 - P( x – M(X)    ) .

Вычислим

.

Все слагаемые D(X) положительные. Отбросим из данной суммы те слагаемые, для которых

( x_i – M(X)) <  тогда:

В последнем неравенстве в правой части остались те слагаемые, для которых

( x_i – M(X))   , ( x_i – M(X))²  ² , откуда D(X)  ² *( p_k+1 + p_k+2 +…+ p_n ) .

Сумма вероятностей p_k+1 + p_k+2 + …. + p_n - есть не что иное, как вероятность того, что:

P(X – M(X)    ), тогда D(X)  ² * P(X – M(X)    ) ,

P(X – M(X)   )  D(X)/² ; P(X – M(X)< )  1 - D(X)/² ,

что и требовалось доказать.

Следствия из неравенства Чебышева:

1. P(X – M(X)|

2. P(X – M(X) )

Доказательство: 1= P(X – M(X) ) + P(X – M(X) ) P(X – M(X) ) + 1 –

P(X – M(X) )

Формулировка неравенства Маркова

Если среди значений случайной величины Х нет отрицательных, то вероятность того, что она примет какое-нибудь значение, превосходящее положительное число А, не больше дроби , т.е.

,

а вероятность того, что она примет какое-нибудь значение, не превосходящее положительного числа А, не меньше , т.е.