Локальная и интегральная теоремы Лапласа.

Если вероятность P в схеме Бернулли не близка к 0 и единице, а число испытаний большое, то тогда вероятность того, что в серии из n испытаний событие появиться K раз вычисляется по формуле:

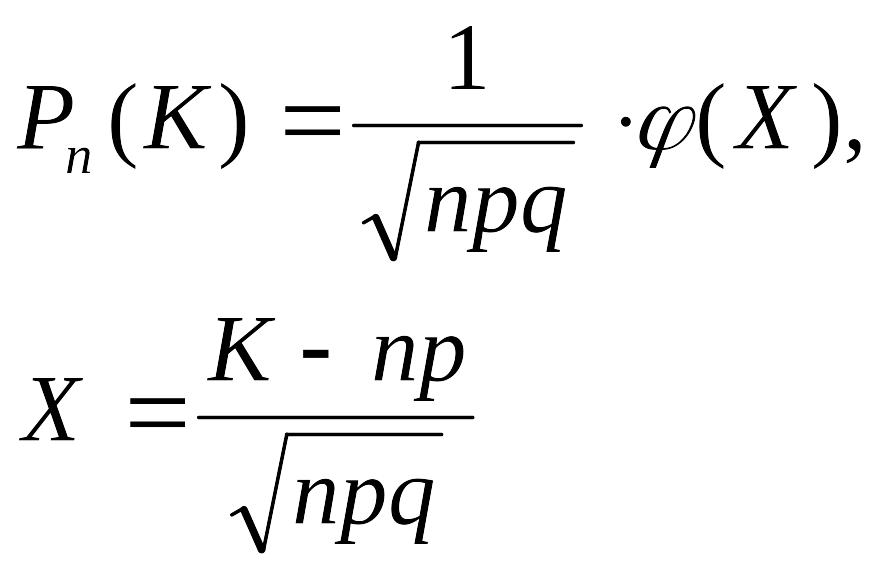
- дифференциальная функция Лапласа.

Для данной функции имеются специальные таблицы значений.

Интегральная теорема Лапласа.

Пусть в схеме Бернулли вероятность P отлична от 0 и не близка к 1, а число испытаний , то тогда вероятность события состоящего в том, что событие A появится не менее, раз и не более, раз вычисляется по формуле:

где

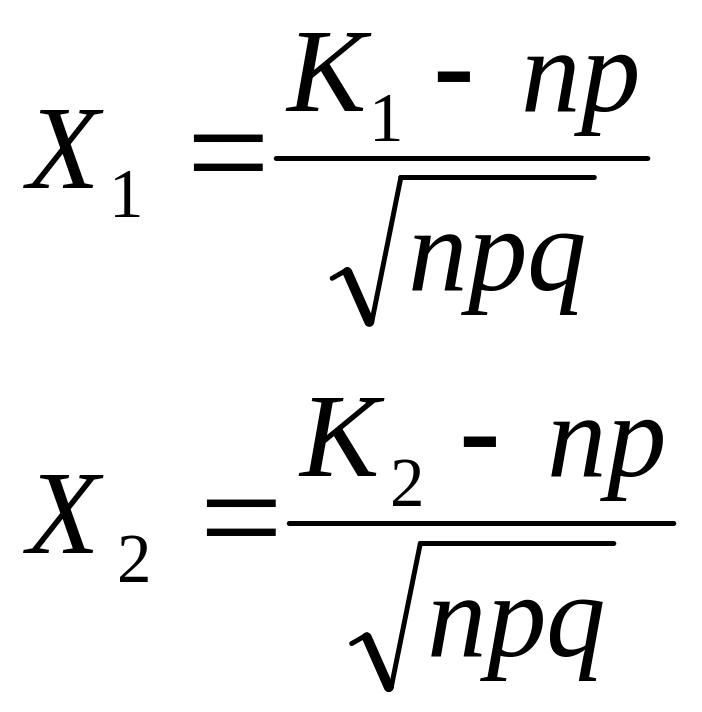
Функция Ф(X) интегральная функция Лапласа. Для нее имеются специальные таблицы значений.

Формула Пуассона.

В случае если в схеме Бернулли число испытаний большое, а вероятность стремиться к 0, то в этом случае пользуются формулой Пуассона:

где .

7.

Дискретные случайные величины.

Одним из основных понятий теории вероятностей является понятие случайной величины.

Случайная величина – величина, которая в результате опыта примет то или иное значение, заранее неизвестное.

Все случайные величины делятся на два типа:

случайные дискретные величины, если возможные значения случайной величины можно пересчитать и их конечное число;

случайные непрерывные величины, если возможные значения случайной величины сплошь заполняют некоторый интервал.

Обычно случайные величины обозначают: , а возможные значения:

Дискретные случайные величины.

Рассмотрим дискретную случайную величину X, которая принимает следующие значения. Задав возможные значения, мы не охарактеризовали случайную величину полностью, т.к. две случайные величины могут иметь одинаковое множество возможных значений. Однако эти значения принимают с разными вероятностями.

Случайная величина будет полностью описана с вероятностной точки зрения, если кроме =возможных значений будут указаны и вероятности, с которыми эти возможные значения допускаются. Основным законом распределения дискретной случайной величины является ряд распределения, который записывается в виде:

Закон распределения случайной величины – любое соотношение между значениями случайной величины и их вероятностями.

Закон распределения случайной величины можно задать и графически, соединив точки прямыми линиями.

Пример:

Самой универсальной характеристикой случайной величины (дискретной или непрерывной), является интегральная функция распределения.

Интегральная функция распределения – вероятность того, что случайная величина примет значение меньше чем X.

Геометрически это означает вероятность того, что случайная величина попадет в полубесконечный интервал .

Пример:

Пусть случайная величина имеет следующий закон распределения:

П оострим интегральную функцию распределения.

8.

Числовые характеристики дискретных случайных величин.

Закон распределения полностью характеризует случайную величину с вероятностной точки зрения. Но во многих задачах нет необходимости такой полной характеристики. Часто достаточно указать такие числовые характеристики как среднее значение, около которого группируются возможные значения, или число, характеризующее степень разбрасывания возможных значений относительно среднего. Такие характеристики - числовые характеристики (дисперсные, среднего квадратического отклонения, математического ожидания).

Математические ожидания.

Математическое ожидание случайной величины – сумма произведений всех ее возможных значений на их вероятности.

Вероятностный смысл математического ожидания состоит в том, что оно приближенно равно среднему ожидаемому значению случайной величины.

Доказательство:

Пусть для случайной величины проверена серия из K испытаний, причем появилось раз, . Среднее арифметическое наблюдаемое значение:

где - частота.

А мы знаем, что если , то. В результате чего мы получаем

Рассмотрим

и

Произведение данных случайных величин - случайная величина.

Арифметическая сумма - случайная величина.

Произведение случайной величины X на C=const – величина , со следующим законом распределения:

Две случайные величины независимы, если закон распределения одной не зависит от того, какое значение приняла другая.

Свойства математического ожидания:

1.

2.

3. ,

4. , X и Y – независимые случайные величины.

5.

Математическое ожидание отклонения случайной величины от ее математического ожидания равно 0.

Замечание: от любого случайного события, каково бы оно не было, всегда можно перейти к случайной величине. Пусть A – случайное событие, которое может произойти или не произойти. Поставим ему в соответствие случайную величину X, причем X=0, если случайное событие произойдет.

Дисперсия и среднеквадратическое отклонение.

Рассмотрим две случайные величины:

Математическое ожидание данных случайных величин одинаково, но возможные значения различны не только по величине, но и по характеру распределения относительно математического ожидания. Если для случайной величины X значения тесно прилегают к математическому ожиданию, то для случайной величины Y возможные значения значительно отстоят от математического ожидания.

Дисперсия – числовая характеристика, характеризующая степень рассеивания значений случайной величины относительно математического ожидания.

Дисперсия случайной величины X – математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Среднеквадратическое отклонение случайной величины X – корень квадратный из дисперсии.

Среднеквадратическое отклонение точно также как и дисперсия характеризует степень рассеивания значений случайной величины относительно математического ожидания.

Найдем дисперсию для случайных величин X и Y, которые мы рассматривали первоначально.

Основные свойства дисперсии:

1.

2.

3.

4.

5.

Доказательство пятого свойства:

Пятым свойством пользуются для вычисления дисперсии.

Понятие о моментах распределения.

Рассмотрим случайную величину, заданную нормальным законом распределения.

Мы видим, что значительно отличается от . Таким образом, переход от к позволил лучше учесть влияние на математическое ожидание того возможного значения, которое велико (в нашем случае X=100), но имеет малую вероятность. Если случайная величина имеет несколько больших значений, которые мало вероятны то, переходя к случайной величине учесть их влияние.

Начальный момент порядка

Центральный момент порядка S – математическое ожидание отклонения случайной величины от математического ожидания в степени S.

9.