
- •Основные понятия и определения теории вероятностей. Классическое определение вероятростей.
- •Статистическая вероятность
- •Сумма событий. Теорема сложения вероятностей.
- •Произведение событий. Теорема умножения вероятностей.
- •Локальная и интегральная теоремы Лапласа.
- •Дискретные случайные величины.
- •Дискретные случайные величины.
- •Числовые характеристики дискретных случайных величин.
- •Непрерывные случайные величины.
- •Числовые характеристики непрерывных случайных величин.
- •Биномиальный закон распределения.
- •Нормальный закон распределения
- •Двумерные случайные величины.Интегральная и дифференциальная функции распределения вероятностей.Одномерные законы распределения.
- •Дискретные случайные величины.
- •Интегральная функция распределения двумерной случайной величины.
- •Вероятность попадания случайной величины в квадрат бесконечных полусумм прямоугольников.
- •Зависимые и независимые случайные величины.
- •Основные понятия математичесКой статистиКи
- •Доверительные интервалы. Доверительная вероятность.
- •Доверительный интервал для оценки математического ожидания при известном .
- •Доверительный интервал для оценки математического ожидания при неизвестном .
- •Статистические гипотезы. Проверка гипотез. Критерий Пирсона.
- •Элементы корреляционного анализа.
- •Линейное програмирование Задачи линейного программирования лесной промышленности.
- •Нормальная кононическая форма задач линейного программирования
- •Геометрический метод решения задач линейного программирования.
- •Симплекс метод
- •Первый этап: построение первоначального базисного плана.
- •Второй этап: проверка (критерий) оптимальности.
- •Третий этап: указание процедуры целенаправленного перехода к следующей крайней точке.
- •Симплекс таблица
- •Метод искусственного базиса в м задачах
- •Транспортная задача.
- •Основные понятия теории массового обслуживания Потоки событий
- •Пуассоновский и простейший потоки. Потоки Пальма и Эрвина.
- •Предельная теорема теории потоков
- •Сложение, разряжение и независимость потоков
- •Марковские процессы
- •Уравнения Колмогорова для вероятностей состояния
- •Эргодические Марковские случайные процессы. Стационарный режим работы системы.
Третий этап: указание процедуры целенаправленного перехода к следующей крайней точке.
Пусть
![]() (первоначальный
базисный план) не оптимален. Перейдем
к новому базисному плану в направлении
наибольшего возрастания целевой функции.
С этой целью среди отрицательных оценок
найдем минимальную оценку
(первоначальный
базисный план) не оптимален. Перейдем
к новому базисному плану в направлении
наибольшего возрастания целевой функции.
С этой целью среди отрицательных оценок
найдем минимальную оценку![]() и вектор,
соответствующий оценке
и вектор,
соответствующий оценке
![]() ,
введем базис. Но из базиса нужно вывести
один из векторов: вектор
,
введем базис. Но из базиса нужно вывести
один из векторов: вектор
![]() ,
который находится из условия
,
который находится из условия
![]() .
.
После чего записываются координаты нового базисного плана:
![]()
Здесь
k
и l
– номера векторов
![]() ,
входящего в новый базис, и
,
выходящего из старого базиса. После
того как мы нашли координаты нового
базисного плана, проверяем этот план
на
,
входящего в новый базис, и
,
выходящего из старого базиса. После
того как мы нашли координаты нового
базисного плана, проверяем этот план
на
оптимальность. В случае если план оптимален то задача решена, если план не оптимален то переходим к новому плану до тех пор пока не получим оптимальный план.
Симплекс итерация - описанный переход от одного базисного плана к другому. 25
Симплекс таблица
При ручной реализации симплекс метода очень удобно пользоваться симплекс таблицей, которая строиться следующим образом:
В
первом столбце записана нумерация
строк, во втором – векторы базиса
,
в третьем
![]() - стоимости соответствующие базисным
столбцам, в четвертом b
– координаты
- стоимости соответствующие базисным
столбцам, в четвертом b
– координаты
крайних точек. На первом этапе это как раз и есть ограничение.
В
самой верхней строке записаны стоимости
соответствующие целевой функции. В
столбцах от
![]() до
до
![]() у нас записана матрица условий на первом
этапе (фактически там записано разложение
векторов по базису), в последней строке
записаны оценки векторов
у нас записана матрица условий на первом
этапе (фактически там записано разложение
векторов по базису), в последней строке
записаны оценки векторов
![]() .
Все эти оценки соответствующие базисным
векторам равны 0, остальные оценки у нас
будут отличны от 0. Оценки
легко вычислить по следующему правилу:
.
Все эти оценки соответствующие базисным
векторам равны 0, остальные оценки у нас
будут отличны от 0. Оценки
легко вычислить по следующему правилу:
Элементы
столбца
![]() перемножаются на соответствующие
элементы
перемножаются на соответствующие
элементы
![]() ,
результат суммируется и из полученной
суммы вычитается
,
результат суммируется и из полученной
суммы вычитается
![]() .
В последний столбец заносятся
.
В последний столбец заносятся
![]() ,
которая определяется следующим образом:
,
которая определяется следующим образом:
Если план у нас неоптимальный, т.е. среди имеются отрицательные, то выбирается среди них наименьшее; если таких несколько, то выбираем одно любое.
Столбец
соответствующий данному
- разрешающий и выделяется двойными или
цветными линиями, после чего делятся
положительные элементы столбца b
на положительные элементы разрешающего
столбца и результаты деления заносятся
в последний столбец. Среди полученных
выбирается минимальное, если таких
несколько, то мы выбираем любое. Строка
соответствующая данному
- разрешающая строка. Вектор![]() нам нужно вывести из базиса, а в базис
ввести вектор
нам нужно вывести из базиса, а в базис
ввести вектор
![]() ,
после чего строим новую таблицу, где
вместо вектора
уже стоит вектор
.
Элементы разрешающей строки делятся
на разрешающий элемент. В разрешающем
столбце стоят все 0, за исключением
разрешающего элемента. Все остальные
элемент, начиная с вектора b,
пересчитываются по правилу прямоугольника:
,
после чего строим новую таблицу, где
вместо вектора
уже стоит вектор
.
Элементы разрешающей строки делятся
на разрешающий элемент. В разрешающем
столбце стоят все 0, за исключением
разрешающего элемента. Все остальные
элемент, начиная с вектора b,
пересчитываются по правилу прямоугольника:
![]()

26
Метод искусственного базиса в м задачах
В случае если у нас задача линейного программирования записана в канонической форме и нет единичного базиса, то вводят искусственный базис, для чего в каждое уравнение добавляют переменные.
Пусть задача записана в виде:
(1)
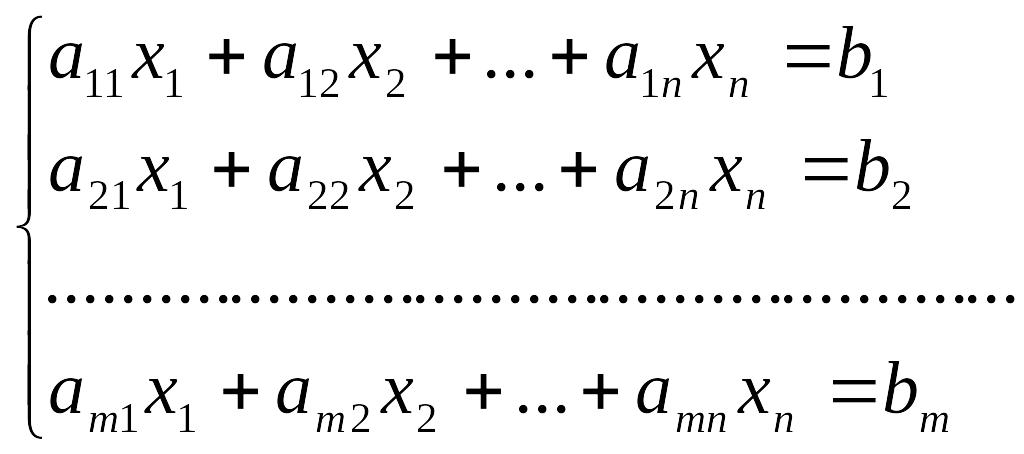 (2)
(2)
Среди векторов условий перейдем к расширенной задаче. Вместо задачи (1) и (2) будем рассматривать следующую задачу:
![]() (3)
(3)
(4)
В расширенной задаче уже имеется единичный базис, который соответствует искусственным переменным. Решая эту задачу симплекс методом, мы через конечное число шагов, либо получим решение, либо покажем неразрешимость данной задачи. Данная М задача связана с исходными следующими утверждениями:
если
в оптимальном плане
![]() расширенной задачи все искусственные
переменные равны 0, то план
расширенной задачи все искусственные
переменные равны 0, то план![]() будет является оптимальным планом для
данной задачи;
будет является оптимальным планом для
данной задачи;
если в оптимальном плане М задачи не все искусственные переменные равны 0, то задача не имеет допустимых решений;
если М задаче неразрешима, то неразрешима и исходная задача.
Симплекс
таблица для М задачи строится аналогично,
за исключением последней строки, причем
столбцы, соответствующие искусственным
переменным, в таблицу не записываются.
Оценки
представляют собой выражение
![]() ,
поэтому определяющим коэффициентом
здесь является коэффициент
,
поэтому определяющим коэффициентом
здесь является коэффициент![]() и если только М отсутствует, то тогда
уже проверяют по величине
.
и если только М отсутствует, то тогда
уже проверяют по величине
.
Замечание: в некоторых случаях не обязательно вводить все искусственные переменные. Если имеется несколько единичных векторов, то нам достаточно ввести искусственные переменные, которые дополняют эти векторы до единичного базиса.
27.
