Ненадежные знания и выводы

В задачах, которые решают интеллектуальные системы, часто приходится применять ненадежные факты и знания, представить которые двумя значениями – истина или ложь – затруднительно.

Пропозициональные графы и система редукций

Основной идеей редукционной системы является поиск доказательства того, что решение данной задачи выводится из решения совокупности ее подзадач.

Другими словами решение задачи в этой системе сводится к нахождению множества альтернативных совокупностей подзадач, каждая из которых дает решение задачи, затем альтернативных совокупностей подзадач этих подзадач и т.д. до тех пор, пока задача не станет разрешимой, то есть решение ее подзадач не станет очевидным, или пока не будет доказано, что задача не имеет решения. Очевидность решения подзадач определяется следующими возможностями:

1. Подзадача носит характер известного утверждения (аксиома).

2. Подзадача может быть решена в системе продукций (например, за один шаг).

3. Подзадача хотя и сложна, но ее решение известно системе на основе предыдущего опыта.

Пространство описаний множества подзадач представляется в виде специального направленного графа G, называемого И-ИЛИ графом, или пропозициональным графом.

С каждой вершиной этого графа связывается описание определенной подзадачи. Дуги этого графа соответствуют операторам сведения задачи к подзадачам. В графе выделяется два типа вершин: конъюнктивные вершины или вершины типа И, которые вместе со своими дочерними вершинами интерпретируются высказыванием «чтобы решить задачу, необходимо решить все ее подзадачи», и дизъюнктивные вершины или вершины типа «ИЛИ», которые вместе со своими дочерними вершинами интерпретируются высказыванием «чтобы решить задачу, достаточно решить одну из ее подзадач.

З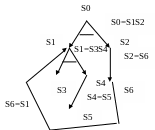 десь S0 – первоначальная задача, для решения которой необходимо решить подзадачи S1 и S2. Для решения S1 необходимо решить подзадачи S3 и S4. Для решения S2 достаточно решить S6. Для решения S4, S6 достаточно решить S5, S1 соответственно. Решение задач S3, S5 считается известным.

В множестве вершин пропозиционального графа выделяют подмножество начальных вершин (задач, которые надо решить) и подмножество конечных вершин (заведомо разрешимых вершин).

С каждой вершиной графа связывается высказывание в виде булевой функции, выраженной в дизъюнктивной нормальной форме и образующейся по следующим правилам: для вершины s, имеющей дочерние вершины

А) Если s – конъюнктивная вершина, то соотнесенная с ней булева функция

где - булевская функция, соотнесенных вершин

Б) Если s – дизъюнктивная вершина, то соотнесенная с ней булевская функция будет:

В) Если s – конечная вершина, то соотнесенная к ней булевская функции истинна, а если вершина не является конечной, но не имеет дочерних вершин, то ее булевская функция ложна.

Г) Если - начальные вершины, то с ними соотносится булевская функция

Очевидно, что решение представляется в виде решающего дерева, являющегося подграфом пропозиционального графа. Соотнесем с каждой дугой ее стоимость. Тогда можно определить критерий оптимизации. Для этого определим стоимость решающего дерева как сумму стоимостей его дуг. Цель оптимизации – найти решающее дерево с минимальной стоимостью.

Удобно определять стоимость вершины графа как стоимость оптимального решающего графа для этой вершины. Стоимость, определенная таким образом, соответствует трудности задачи.

Будем предполагать, что стоимость вершин можно оценить (не зная соответственно решающих деревьев) при помощи эвристической функции h. Эти оценки используются для управления поиском. Алгоритм начинает свою работу со стартовой вершины и, распространяя поиск на уже просмотренных вершинах на их преемников, будет постепенно наращивать дерево поиска. Этот алгоритм будет строить дерево даже в том случае, когда граф не является деревом, при этом граф будет разворачиваться в дерево за счет дублирования своих отдельных частей.

Для продолжения поиска выбирается наиболее перспективное дерево кандидат.

Обозначим через H(B) оценку трудности вершины B. Для самой верхней вершины H(B) просто совпадает с h(B). С другой стороны, для оценки внутренней вершины не обязательно использовать непосредственное значение h, поскольку существует дополнительная информация об этой, известны ее преемники. Следовательно, можно оценить трудность внутренней ИЛИ – вершины как

где - стоимость дуги, ведущей из B в .

Трудность И – вершины B можно приближенно оценить как:

Будем называть H – оценку внутренней вершины возвращенной оценкой.

Более практичной с точки зрения поиска является другая величина F, которую можно определить в терминах H следующим образом. Пусть B1 вершина предшественник вершины B в дереве поиска, причем стоимость дуги, ведущей из B1 в B, равна c(B, B1), тогда положим:

F(B)=c(B, B1) + H(B).

Пусть B1 – родительская вершина B, а - ее дочерние вершины, тогда в соответствии с определением F и H, имеем:

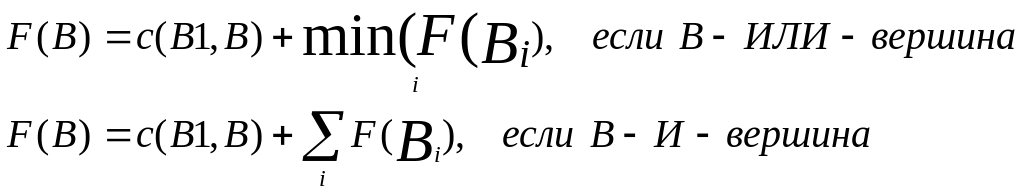
Хотя стартовая вершина A и не имеет предшественников, будем считать, что стоимость ведущей в нее виртуальной дуги равна 0. Если положить h равным 0 для всех вершин И/ИЛИ дерева, то для любого найденного оптимального решающего дерева окажется, что его стоимость, то есть стоимость его дуг в точности равна F(A).

На любой стадии поиска каждый преемник ИЛИ вершины соответствует некоторому альтернативному решающему дереву кандидату. Процесс поиска всегда принимает решение продолжать просмотр того дерева кандидата, для которого F –оценка минимальна. Рассмотрим следующий пример.

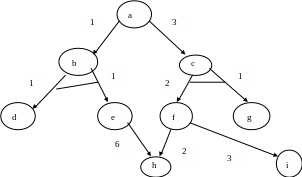
В начале дерево поиска состоит из одной стартовой вершины – вершины a, далее дерево растет, пока не будет найдено решающее дерево.

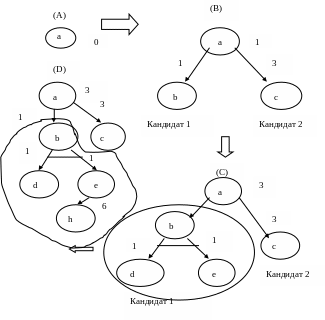
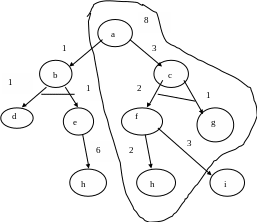
После распространения поиска из первоначального дерева (А) получается дерево (В). Вершина a – это ИЛИ вершина, поэтому мы имеем два решающих дерева кандидата: b, c. ПосколькуF(b) = 1 < 3 =F(c), для продолжения поиска выбирается альтернатива b. Процесс будет продолжаться до тех пор, пока не произойдет одно из двух событий:

1. F – оценка вершины b станет больше, чем F –оценка ее конкурента c

2. Обнаружится, что найдено решающее дерево

В связи с этим, начиная просмотр дерева кандидата b, устанавливаем верхнюю границу для F(b): F(b)  3 = F(c). Сначала порождаются преемники d и e вершины c (C), после чего оценка b возрастает до 3. Так как это значение не превосходит верхнюю границу, рост дерева кандидата c в b продолжается. Вершина d является целевой вершиной, а после распространения поиска из вершины g на один шаг получаем дерево (D). В этот момент выясняется, что F(b) = 9 > 3, и рост дерева b прекращается. В результате процесс поиска не успевает осознать, что h – это тоже целевая вершина и что порождено решающее дерево. Вместо этого происходит переключение активности на конкурирующую альтернативу c. Поскольку в этот момент F(b) = 9, устанавливается верхняя граница для F(c) равная 9. Дерево кандидат с корнем c наращивается (с учетом установленного ограничения) до тех пор, пока не возникает ситуация (E). Теперь процесс поиска обнаруживает, что найдено решающее дерево (включающее в себя целевые вершины), на чем поиск заканчивается. Обратим внимание, что в качестве результата процесс поиска выдает наиболее дешевое из двух возможных решающих деревьев.