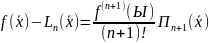- •1. Предмет и метод вычислительной математики
- •2. Метод исключения Гаусса
- •3. Метод Гаусса с выбором главного элемента
- •6. Метод итерации. Для решения слау. Оценка погрешности
- •7. Метод Зейделя.
- •1 3. Метод итераций для решения трансцендентных уравнений. Сходимость
- •14. Метод итераций для решения трансцендентных уравнений. Оценка погрешности
- •15. Метод итерация для системы 2х уравнений
- •16. Метод Крылова
- •17. Определение собственных векторов в методе Крылова
- •18. Метод Данилевского
- •19. Вычисление собственных векторов по методу Данилевского
- •20. Нахождение наибольшего по модулю собственного значения матрицы и соответствующего собственного вектора
- •27. Оценка погрешности формулы ньютона
- •32. Формула трапеций
- •33. Формула Симпсона
- •34. Общая формула трапеций( правило трапеций)
- •35. Общая формула Симпсона (параболическая формула)
- •36.Правило Рунге
- •37. Квадратурные формулы наивысшей степени точности (формула Гаусса)
- •38. Классификация численных методов приближенного решения обыкновенных диффуров
- •39. Метод Эйлера
- •40. Модифицированный метод Эйлера
16. Метод Крылова
пусть есть матрица А = Matrix[n](aij) (1)
 -
называется собственным значением
матрицы А если:
-
называется собственным значением
матрицы А если:
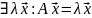 ,(2)
,(2)
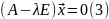
det(A-
 )
= 0 = (-1)n(
)
= 0 = (-1)n( -
p1
-
p1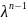 - p2
- p2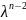 - .... - pn)
= 0
- .... - pn)
= 0
проблема собственных значений бывает полная и частная (найти все или нет)
Метод Крылова
А обращает в 0 свой характеристический многочлен
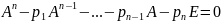 Pn
- коэффициенты
Pn
- коэффициенты

вообще говоря суть метода Крылова - найти P1 .. Pn
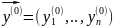 (4)
=>
(4)
=>
 (5)
(5)
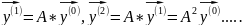
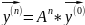 (6),
подставим (6) в (5) и получим
(6),
подставим (6) в (5) и получим
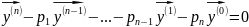 (7)
(7)
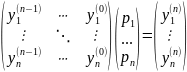 (8)
(8)
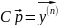 (9)
(9)
если матрица С получилась вырожденной то неудачно взято начальное приближение, нужно замутить бектрекинг с точкой возврата на выбор начального приближения
вывод:
это метод вычисления Р
алг в общем виде:
1) берем y0, строим (6)
2) составляем система (9), решаем ее, например, гауссом, получили p1.. pn
3) после метода Крылова находим
17. Определение собственных векторов в методе Крылова
есть

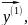 ..
..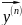 (10) p1....
pn
(10) p1....
pn

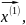 ..
..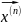 (11) - линейно не зависимые вектора базиса.
искомые собственные вектора(СВ)
(11) - линейно не зависимые вектора базиса.
искомые собственные вектора(СВ)
разложим
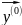 по СВ
по СВ
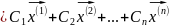 (12)
(12)
 (13)
(13)
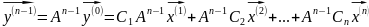
учтем
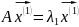 ,
,
 ,....,
,....,
 ,
из (13) получим
,
из (13) получим
 (14)
(14)
из (12) и (14) имеет

 (15)
(15)

и
причем
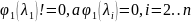

и по схеме Горнера (???wtf)
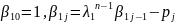 ,
j=1..n-1
,
j=1..n-1
мы построили линейную комбинацию для x1
для
остальных
 (19)
(19)
18. Метод Данилевского
До определения коэффициентов характеристического уравнения матрицу A/* A= matrix[n](aij)*/ с помощью n-1 преобразований подобия заменяют подобной ей матрицей Фробениуса
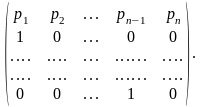 = P
= P
где pi - коэффициенты ее характеристического многочлена
S: P = S-1AS
На первом этапе делаю следующее:
(an1,an2,..,ann) -> ( 0,0,...,1,0), при условии что ann-1 !=0
потом все эл-ты n-1 столбца делим на ann-1 (an1,an2,..,1,ann) и теперь из каждого столбца вычитают n-1й умноженный на anj т.е.

где

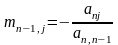
B=AMn-1

где
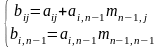
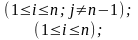

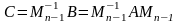 (матрица
С
подобна матрице А);
(матрица
С
подобна матрице А);
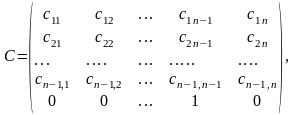
где
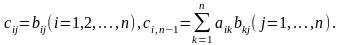
Шаг 2:
Матрицу
С преобразуем в D
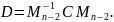 Теперь повторяем все вышесказанные
для n-2
столбца и так далее n-1
раз и получим форму Фробениуса
Теперь повторяем все вышесказанные
для n-2
столбца и так далее n-1
раз и получим форму Фробениуса
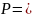
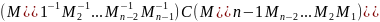
теперь
находим
 :
:
- аналитически
- метод хорд\касательных и т.д
- Лобачевского
19. Вычисление собственных векторов по методу Данилевского
λ - собственные значения которые уже известны
дано λ,А,Р
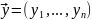 -
собственный вектор P(см
18й билет)
-
собственный вектор P(см
18й билет)
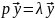
 =
0
=
0
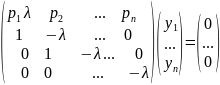
получим
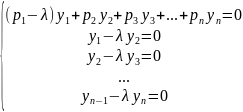

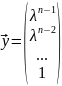

 ...
...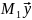
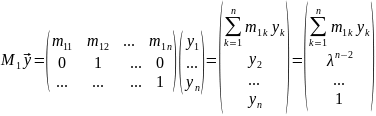
20. Нахождение наибольшего по модулю собственного значения матрицы и соответствующего собственного вектора
 (A
- λE) =0
(A
- λE) =0

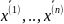 -
собственные вектора
-
собственные вектора
Определение
Первым собственным значением
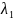 называется наибольшее по модулю
собственное значение матрицы А
называется наибольшее по модулю
собственное значение матрицы А
нахождение 1ого СЗ является частной проблемой собственных значений
пусть
у А ∃!
собственное значение тогда
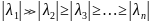
Теорема Перрона
если А - действително(е,я?????) и все эл-ты А >0 то - действительное число
Итерационный метод нахождения 1ого СЗ
возьмем произвольный вектор и разложим по собственному вектору
 (1)
(1)

A - итерация вектора
а
считать мы будем


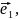 ...,
...,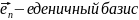 .
разложим N-ую
итерацию по этому базису
.
разложим N-ую
итерацию по этому базису
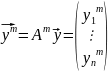 ,
m
=1,2,3....
,
m
=1,2,3....
/*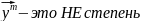 */
*/
Собственный вектор разложим по базису

(3) подставим в (2)

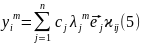

будем
полагать что с1
!=0
 - этого всегда можно добиться
- этого всегда можно добиться

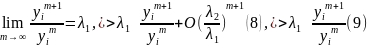
Вывод:
1)
берем произв. вектор
 (m=0)
(m=0)
2)
вычисляем m+1-ию
итерацию
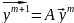
3) находим N-ое приближение 1ого СЗ
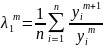
4) находим (n+1)ое приближение
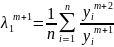
5) сравниваем
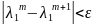
если
условие выполняется то
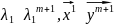
если нет то в пункт 6
6)
нормируем вектор
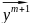
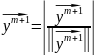
21. Интерполирование функцией

22. конечные разности и их свойства

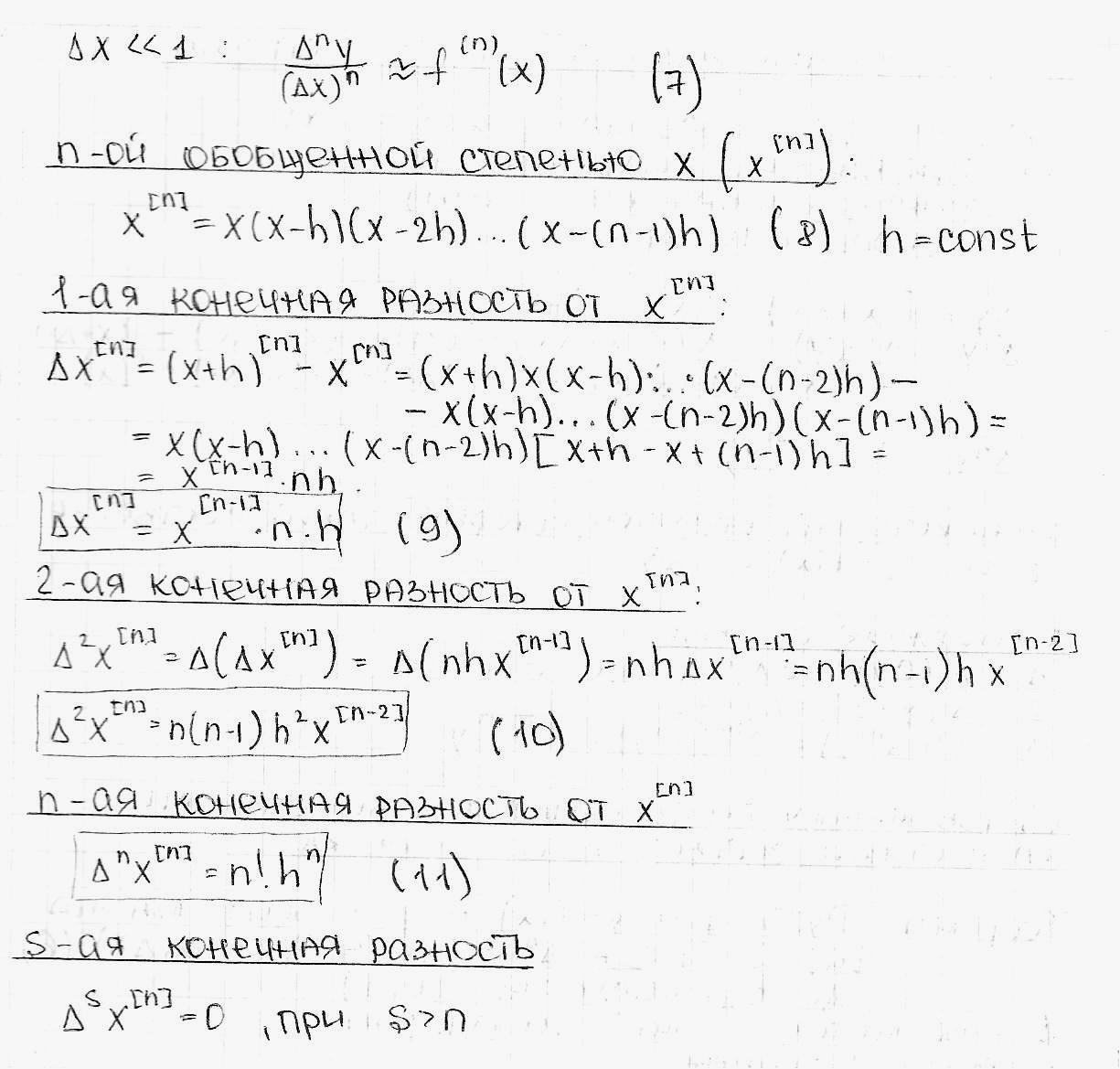
23. первая интерполяционная формула ньютона


24. вторая интерполяционная формула ньютона


25. интерполяционная формула лагранжа


26. оценка погрешности формулы Лагранжа
Rn(x)= f(x) - Ln(x)
Rn(xi) =0 i=0..n
будем изучать что на [a;b] фнк имеет до n+1 производные
введем ψ(x) = f(x) - Ln(x) - k Πn+1(x) (10) //k=? = const
ψ(x) имеет n+1 корень
подберем
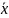 так чтобы ψ(
)
=0,
так чтобы ψ(
)
=0,
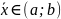
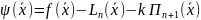 ,
,
 !=0
!=0
 (11)
(11)
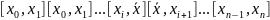
Правило Ролля ( Тролля))
найдется
такая точка Ы что
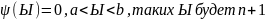 тогда на концах [Ыi,
Ыi+1]
найдется такая формула
тогда на концах [Ыi,
Ыi+1]
найдется такая формула

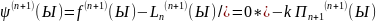 =
=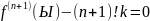 (12) =>
(12) =>
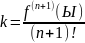 (13)
(13)
если
сравнить (11) и (13) то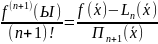 ,
,