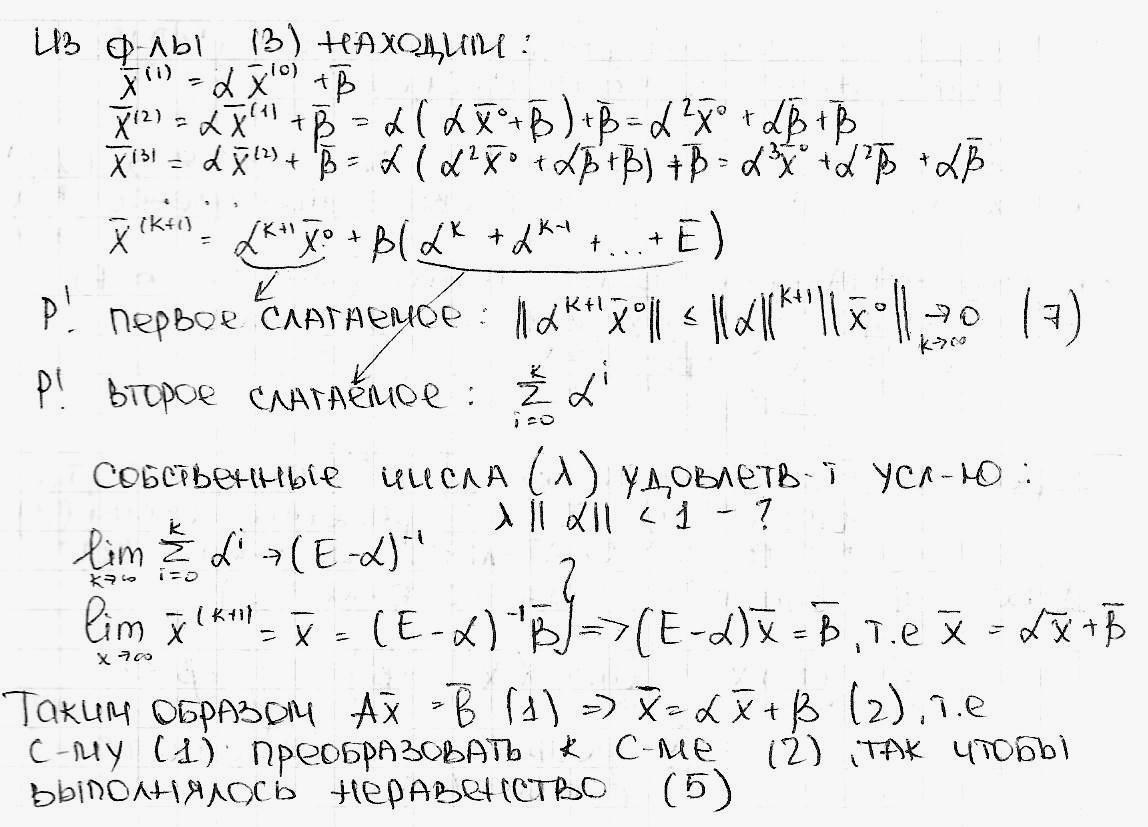3. Метод Гаусса с выбором главного элемента

Выбираем ненулевой, наибольший по модулю, элемент матрицы системы 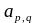. Этот элемент называется главным элементом, а строка, его содержащая – главной строкой. Вычисляем множители для всех строк ,

.

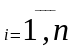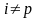
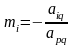К каждой i-ой строке прибавляем p-ую, умноженную на соответствующий множитель 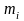, после чего q-ый столбец системы (кроме элемента ) будет состоять из нулей. Отбрасываем этот столбец и главную p-ую строку. Получаем систему уравнений порядка, с которой проделываем ту же операцию, и т.д. до системы уравнений первого порядка. Для получения решения объединим в систему все главные строки, начиная с последней, из которой последовательно шаг за шагом находим все неизвестные. Заметим, что метод Гаусса является частным случаем метода главных элементов, а схема метода Гаусса получается, если за главный элемент всегда выбирать левый верхний элемент соответствующей матрицы. При использовании метода Гаусса производится 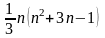операций умножения и деления и 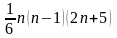вычитаний, то есть всего 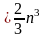операций.

Замечание 1. Надлежащей перестановкой строк и столбцов на каждом шаге прямого хода в методе главных элементов можно получить систему уравнений с треугольной матрицей. Для этого необходимо главный элемент перемещать в первую строку и в первый столбец соответствующей матрицы. При этом нужно не забывать, что при перестановке столбцов изменяется нумерация неизвестных.

4. Метод прогонки

Метод прогонки применяется для решения систем линейных алгебраических уравнений с трехдиагональной матрицей. Пусть система уравнений имеет вид:

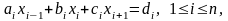(3.1)

причем 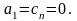Матрица этой системы трехдиагональна, т.е. ненулевыми в ней являются только элементы главной диагонали и двух соседних

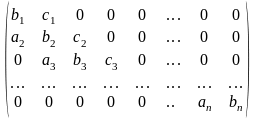
Решение системы уравнений (3.1) ищем в виде

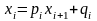(3.2)

Используя выражение (3.2) для узла с номером 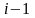, исключим неизвестное 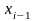из 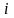-ого уравнения системы (3.1)

,

откуда получим

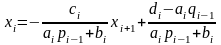(3.3)

Сравнивая соотношение (3.3) с (3.2), выводим рекуррентные формулы для прогоночных коэффициентов

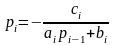, , (3.4)

вычисление которых составляет прямой ход метода прогонки. По формулам (3.4) вычисляются 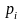и для . Для определения коэффициентов 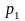и возьмем первое уравнение системы (3.1)

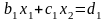
и разрешим его относительно :

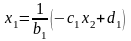. (3.5)

Сравнивая (3.5) с (3.2) при 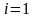, получаем

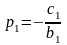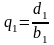, . (3.6)

Обратный ход начинается с определения 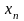. Возьмем последнее уравнение системы (3.1) и формулу (3.2) при 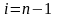. Получится система двух уравнений с двумя неизвестными ,

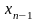
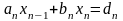
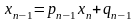
из которой находим

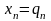. (3.7)

Затем воспользуемся рекуррентными формулами (3.2) для обратного хода и найдем последовательно 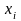для .

Т. О достаточном условии сходимости метода прогонки

если выполняется условие преобладания диагональных элементов т.е.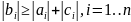

если ∀i соблюдается строгость неравенства то в формулах(6) не возникают /0 и (2) имеет 1 ре6шение

док-во

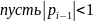тогда

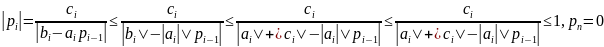
5. Метод простой итерации метод Якоби

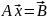(1)

(1) преобразуем к эквивалентной системе вида:

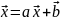(2)

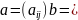
выберем начальное приближение

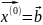
(3)

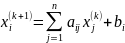, i = 1..n (4)

Теорема 1 если последовательность векторов 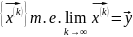- сходится то 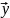есть решение системы (2) , а следовательно и (1)

док-во

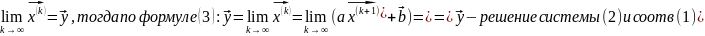
чтд.

Опр В простой квадратной матрице nxn первая каноническая форма

)

Вторая каноническая норма )

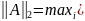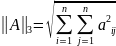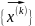сферическая( эвклидова ) норма Теорема 2 Для сходимости приближений к точному решению х системы уравнений (2) достаточно чтобы какая либо каноническая норма матрицы a была <1

док-во: пусть 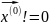- начальное приближение