Моделирование с помощью

Определение порядка модели достаточно просто. Оно основано на следующем свойстве автокорреляционной функции модели скользящего среднего, которое мы рассматривали ранее:

Следовательно, достаточно найти такое значение , для которого выборочная автокорреляция 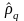отлична от нуля, а выборочные автокорреляции большего порядка близки к нулю.

Для оценки параметров модели обычно используют метод максимального правдоподобия.

Адекватность построенной модели проверяется тем же способом, что мы рассматривали выше для модели . Однако, в случае модели с параметрами, статистика 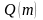будет ассимптотически иметь распределение с степенями свободы.

7.Моделирование с помощью arma(p,q)

Моделирование с помощью аналогично вышеизложенному.

При определении порядка модели используют выборочную частную автокорреляционную и выборочную автокорреляционную функции. Оценку параметров производят с помощью метода максимального правдоподобия. Статистика Льюнга-Бокса:

,

используемая для приверки адекватности построенной модели, имеет ассимптотически распределение с степенями свободы.

Остановимся подробнее на особенностях прогнозирования с помощью модели , поскольку нам понадобится этот аспект при расчете величины 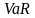(Value at Risk). Обозначим через текущий момент времени. Прогноз для момента времени 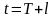, построенный на основе всей доступной к текущему моменту времени информации обозначим через , т.е.

.

Прогноз на один шаг вперед:

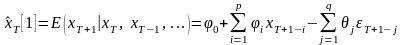
с остатками (ошибками прогнозирования)

,

имеющими вариацию

.

Прогноз на шагов вперед:

,

где и могут быть получены последовательно.

Из -представления для модели получаем:

,

откуда для ошибки прогнозирования имеем:

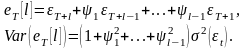
8.Сезонные модели

Некоторые финансовые временные ряды, такие, например, как квартальные данные о прибыли на акцию, данные об объемах продаж, демонстрируют некоторую периодичность в своем поведении. Для того, чтобы провести объективное сравнение таких данных между собой необходимо прежде всего удалить эту сезонную компоненту. В то же время при прогнозировании поведения таких финансовых временных рядов сезонность является важной компонентой прогноза.

Обычно подразумевается, что финансовый ряд демонстрирует периодичность в своем поведении с периодом , если наблюдается сходство в поведении финансового ряда через каждые временных интервалов. Так, для квартальных данных о прибыли на акцию 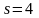(квартала), для данных об объемах продаж 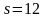(месяцев).

Рассмотрим финансовый временной ряд , отражающий, например, квартальные данные о прибыли на акцию. Выборочная автокорреляционная функция, изображенная на рисунке (3.5.1), демонстрирует высокий уровень корреляции временного ряда.

Рис. 3.5.1. Выборочная автокорреляционная функция для

В случае наличия сильной корреляции необходимо рассмотреть ряд разностей первого порядка:

.

На рисунке 3.5.2 изображена выборочная автокорреляционная функция ряда . Как видно из рисунка, автокорреляция очень сильная при значении лага, кратном четырем. Это и есть эмпирическое подтверждение наличия сезонности с периодом .

Рис. 3.5.2. Выборочная автокорреляционная функция для