Модель Шарпа – Линтнера

В модели ценообразования финансовых активов Шарпа – Линтнера финансовый рынок состоит из безрискового актива с доходностью и рисковых активов с доходностями .

Сделаем следующие предположения относительно и . Пусть доходность хотя бы одного рискового актива отличается от безрисковой доходности: , а матрица ковариаций положительно определена, т.е. для любого портфеля : 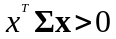. Тогда эффективный портфель -го инвестора существует и единственен и в соответствии с (3.1.10) его можно определить следующим образом:

,

где – показатель терпимости инвестора к риску, – портфель с минимальной дисперсией, – вектор, у которого:

Тогда совокупный спрос на рынке будет представлен портфелем:

, (3.2.1)

где – начальный капитал -го инвестора. Подставляя выражение для 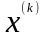в (3.2.1), получаем:

Портфель принадлежит эффективному множеству, следовательно он удовлетворяет системе уравнений (3.1.9), т.е.:

где .

Из уравнений (3.2.2) и (3.2.3) получаем:

, (3.2.5)

где – доходность -го рискового актива, – доходность портфеля .

Далее, умножая (3.2.2) на , (3.2.3) на , складывая полученные выражения и учитывая (3.2.2) и (3.2.4), получаем:

. (3.2.6)

Из (3.2.5) и (3.2.6) получаем уравнение Шарпа – Линтнера:

где

. (3.2.7)

Так как рынок находится в равновесии, то вектор также будет характеризовать и предложение на финансовом рынке, т.е. является рыночным портфелем, в котором доля каждого актива равна отношению его совокупной рыночной стоимости (произведению текущей рыночной стоимости актива на количество его единиц в обращении) к сумме совокупных рыночных стоимостей всех активов на финансовом рынке:

,

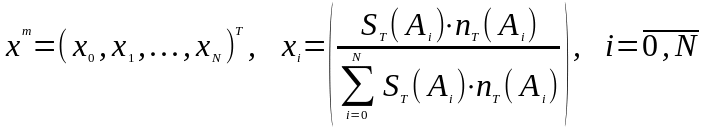где и – соответственно рыночная стоимость и количество единиц актива в момент времени .

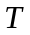На практике в качестве доходности рыночного портфеля используется значение финансовых индексов (Dow Jones, Standart & Poor's 500, индексы NYSE, NASDAQ и т.д.), дающих обобщенную информацию о состоянии финансового рынка.

Уравнение Шарпа – Линтнера (3.2.7) можно переписать в следующем виде:

(3.2.8)

Разность называется премией за риск для актива , а – премией за риск для рыночного портфеля. Величина называется коэффициентом бета актива .

16. Модель ценообразования финансовых активов Блэка.

Модель ценообразования финансовых активов основана на следующих предположениях.

• Финансовый рынок и действия на нем индивидуального инвестора описываются моделью Марковитца.

• На рынке действуют инвесторов с однородными ожиданиями, т.е. инвесторы одинаково оценивают математическое ожидание и дисперсию доходностей рисковых активов: , и имеют одинаковый временной горизонт в один период .

• Рынок находится в равновесии, т.е. спрос на финансовые активы равен их предложению.

В модели Блэка рассматривается финансовый рынок, на котором отсутствует безрисковый актив. Вместо него вводится так называемый портфель с нулевым коэффициентом бета.

Пусть ожидаемая доходность как минимум для двух рисковых активов различна: , а матрица ковариаций положительно определена, т.е. для любого портфеля : . Предположения относительно и позволяют сделать вывод, что для каждого инвестора с показателем терпимости к риску существует и единственен эффективный портфель , который исходя из (3.1.7) представим в виде:

,

где – портфель с минимальной дисперсией, а .

Совокупный спрос на рынке будет равен рыночному портфелю, соответствующему совокупному предложению:

, (3.2.9)

где – начальный капитал -го инвестора. Подставляя выражение для в (3.2.9), получаем:

Портфель принадлежит эффективному множеству, следовательно он удовлетворяет системе уравнений (3.1.5), т.е.:

Рассмотрим портфель 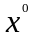(рис. 3.2.2) из достижимого множества, который имеет наименьшую дисперсию среди портфелей, некоррелированных с рыночным портфелем , т.е. является решением задачи:

Имеем:

,

где – дисперсия рыночного портфеля.

Умножим (3.2.10) на и вычтем из полученного выражения (3.2.10), умноженное на . Учитывая (3.2.11) и , получаем:

. (3.2.12)

Далее, подставим в (3.2.10) выражение для , полученное из (3.2.10), умноженного на , с учетом (3.2.11) и . Тогда получим:

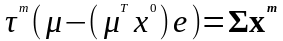. (3.2.13)

Объединяя (3.2.12) и (3.2.13), приходим к уравнению Блэка:

где ,

где – доходность портфеля , который называется портфелем с нулевым коэффициентом бета (рис. 3.2.1), – доходность рыночного портфеля. Величина называется премией за риск для актива , а – премией за риск для рыночного портфеля.

Рис. 3.2.1. Рыночный портфель и портфель с нулевым коэффициентом бета

17. Оценка параметров модели Шарпа – Линтнера

Модель ценообразования финансовых активов рассматривается в рамках одного временного периода . Однако можно использовать данные о значениях доходностей активов и рыночного портфеля в моменты времени для оценки коэффициентов бета.

Рассмотрим уравнение Шарпа – Линтнера, записанное в следующем виде:

.

Обозначим через вектор 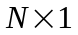премий за риск для активов в момент времени 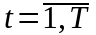, через – премию за риск для рыночного портфеля в момент , т.е.:

Сделаем следующие предположения.

1. Премии за риск для актива , т.е. 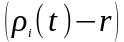, , являются независимыми и одинаково распределенными случайными величинами. Совместное распределение премий за риск для активов , т.е. распределение случайного вектора , является нормальным.

2. Коэффициенты не зависят от времени.

3. Соотношения между и , являются линейными, т.е. их можно описать следующим уравнением регрессии:

, (3.2.14)

где – векторы коэффициентов регрессии, – вектор ошибок.

4. Ошибки являются независимыми одинаково распределенными случайными величинами, для которых выполнены условия гомоскедастичности, т.е. независимости дисперсии от :

~ ,

.

5. – условие независимости доходности рыночного портфеля и вектора ошибок.

Оценим параметры и с помощью метода наименьших квадратов и метода максимального правдоподобия. При этом предположение 1 о распределении премий за риск является обязательным только при использовании метода максимального правдоподобия.

В соответствии с методом наименьших квадратов (ordinary least squares method, OLS), оценка параметров и осуществляется исходя из минимизации функционала:

Необходимые условия экстремума:

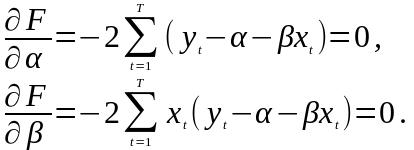
дают следующие оценки параметров и :

где .

Оценка для , полученная методом наименьших квадратов, равна¹:

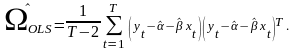
Оценим параметры и , используя метод максимального правдоподобия (maximum likelihood, ML). Для этого рассмотрим логарифмическую функцию правдоподобия, равную логарифму от совместной плотности распределения случайных векторов при заданных значениях , найдем векторы ее частных производных по неизвестным параметрам и , приравнивая которые к нулю, получим оценки для и .

Плотность нормального распределения случайного вектора при известном для каждого наблюдения задается функцией:

.

Отсюда совместная плотность распределения независимых случайных векторов :

Логарифмическая функция правдоподобия:

(3.2.15)

Приравняем к нулю частные производные:

Решая систему уравнений, получаем оценки для и :

(3.2.16)

Оценки для и , полученные методом наименьших квадратов и методом максимального правдоподобия, совпадают. Будем обозначать их в дальнейшем и . Они являются:

1. несмещенными, так как:

2. состоятельными, т.е. сходится по распределению к , или

;

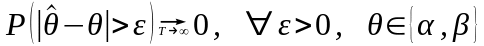3. асимптотически нормальными, т.е. при , где – асимптотическая информационная матрица Фишера . Оценить матрицу ковариаций для полученных оценок и можно с помощью информационной матрицы Фишера:

.

Имеем:

,

где ;

4. асимптотически эффективными, т.е. , где – любая другая состоятельная и асимптотически нормальная оценка параметра .

Что касается полученных оценок и для параметра , то является состоятельной, а состоятельной и несмещенной оценкой.

18. Проверка гипотезы о свободном члене в уравнении регрессии модели Шарпа – Линтнера.

Рассмотрим уравнение регрессии , введенное в предыдущем параграфе. Полученные оценки параметров и асимптотически имеют нормальное распределение:

,

.

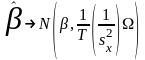Необходимо проверить гипотезу , которая вытекает из сопоставления уравнения регрессии с уравнением Шарпа – Линтнера .

Для проверки гипотезы рассмотрим следующие тесты:

• тест Вальда, который использует оценки параметров в модели без ограничений (примером модели без дополнительных ограничений на параметры является так называемая рыночная модель ²);

• тест отношения правдоподобия, который использует оценки параметров в модели без ограничений и в модели с дополнительными ограничениями на параметры.

Тест Вальда основан на критической статистике:

,

которая асимптотически имеет распределение с степенями свободы в соответствии с размерностью вектора . Если матрица ковариаций ошибок неизвестна, то можно использовать ее состоятельную оценку .

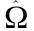Тест отношения правдоподобия использует для проверки нулевой гипотезы оценки параметров уравнения регрессии как с ограничением, так и без него. Помимо логарифмической функции правдоподобия (3.2.15) и полученных с ее помощью оценок (3.2.16) для параметров и в модели без ограничений, для построения критической статистики необходимо также рассмотреть логарифмическую функцию правдоподобия для уравнения регрессии с ограничением , т.е.:

, (3.2.17)

для которой получаем следующие оценки:

При построении критической статистики теста отношения правдоподобия используется разница максимумов логарифмических функций правдоподобия для модели с ограничением и модели без ограничения:

,

где – значение логарифмической функции правдоподобия (3.2.15), при котором вместо неизвестных параметров и используются их оценки (3.2.16), обеспечивающие максимум 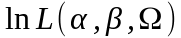; – максимальное значение функции правдоподобия для уравнения регрессии с ограничением.

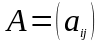Заметим далее, что в соответствии с известными из линейной алгебры равенствами и , где – оператор взятия следа матрицы , получаем:

где – единичная матрица размера . Аналогичным образом, используя свойства следа матрицы, получаем, что . Следовательно:

.

Критическая статистика асимптотически имеет распределение. Количество степеней свободы определяется как разность 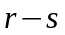между размерностью всего параметрического множества и размерностью 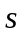его подмножества, в котором верна нулевая гипотеза. Размерность равна количеству независимых параметров модели без ограничений, а – числу независимых параметров модели с ограничениями.

Независимые параметры модели без ограничений представлены параметрами матрицы ковариаций ошибок , параметрами вектора и параметрами , а модель с ограничениями имеет на независимых параметров меньше в соответствии с размерностью вектора . Следовательно, критическая статистика будет иметь степеней свободы.

19. Оценка параметров и проверка гипотез в уравнении регрессии модели Блэка

Рассмотрим уравнение Блэка:

, (3.2.18)

где .

В данной модели параметры, которые необходимо оценить, представлены коэффициентами бета для активов, т.е. , и ожидаемой доходностью портфеля с нулевым коэффициентом бета , который мы обозначили через .

Пусть – вектор доходностей рисковых активов в момент времени , а – доходность рыночного портфеля в момент , т.е.:

Сделаем следующие предположения:

1. Доходности актива во времени, т.е. 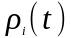, , являются независимыми и одинаково распределенными случайными величинами. Совместное распределение доходностей активов , т.е. распределение случайного вектора , является нормальным. (Данное предположение не требуется в случае использования метода наименьших квадратов).

2. Коэффициенты не зависят от времени.

3. Соотношения между и , являются линейными, т.е. их можно описать следующим уравнением регрессии:

,

где – векторы коэффициентов регрессии, – вектор ошибок.

4. Ошибки являются независимыми одинаково распределенными случайными величинами, для которых выполнены условия гомоскедастичности:

~ ,

.

5. – условие независимости доходности рыночного портфеля и вектора ошибок.

Используя метод наименьших квадратов или метод максимального правдоподобия, получаем оценки параметров и , совпадающие с оценками этих параметров для модели Шарпа – Линтнера:

Разница между полученными оценками для разных моделей будет состоять лишь в том, что в модели Шарпа – Линтнера под и понимаются премии за риск, а в модели Блэка – реальные доходности.

По аналогии с оценками в уравнении регрессии для модели Шарпа – Линтнера оценки для и будут асимптотически нормальными:

,

.

В рамках модели Шарпа – Линтнера проверяется следующая гипотеза:

,

где

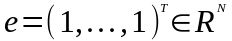
Функция правдоподобия для уравнения регрессии модели Шарпа – Линтнера с ограничением :

Дифференцируя ее по и и приравнивая частные производные к нулю, получаем оценки для модели с ограничением:

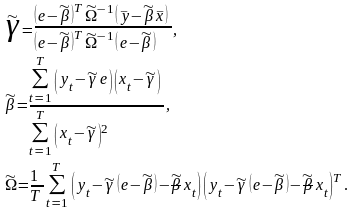(3.2.19)

Критическая статистика теста отношения правдоподобия:

имеет асимптотически распределение с степенями свободы. По сравнению с моделью Шарпа – Линтнера, критическая статистика теряет одну степень свободы, так как модель с ограничениями имеет на независимый параметр меньше:

	Количество независимых параметров
	модель без ограничений	модель с ограничениями
Матрица ковариаций ошибок
Вектор		0
Вектор
Параметр	0	1

Использование теста отношения правдоподобия в данной форме связано с определенными неудобствами, вызванными тем, что вычисление оценок параметров и требует применения итерационных методов, поскольку оценки (3.2.19) являются взаимозависимыми. Рассмотрим способ, позволяющий преодолеть этот недостаток.³

Для модели Блэка:

,

имеем следующее уравнение регрессии:

, (3.2.20)

в котором независимой (объясняющей) переменной является , а зависимой (объясняемой) – .

Оценки модели (3.2.20) без ограничений, полученные с помощью метода максимального правдоподобия:

(3.2.21)

Максимальное значение логарифмической функции правдоподобия для модели без ограничений:

не зависит от .

Оценки модели (3.2.20) с ограничением :

(3.2.22)

позволяют вычислить максимальное значение логарифмической функции правдоподобия с ограничением:

,

которое зависит от .

Простой подстановкой формул (3.2.21) и (3.2.22) легко проверить, что выражается через и следующим образом:

.

Тогда получаем:

Заметим, что

,

тогда

Критическая статистика теста отношения правдоподобия:

Минимизация разности по позволяет найти оценку для , полученную методом максимального правдоподобия. В силу свойств логарифмической функции минимизация равносильна максимизации функции:

,

которая в общем виде представима следующим образом:

,

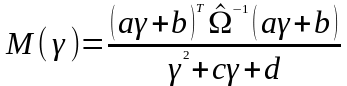где и

Значение , соответствующее максимуму , определяется исходя из решения уравнения , т.е.

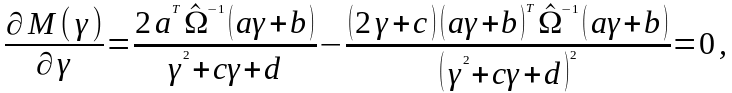
откуда получаем квадратное уравнение относительно :

,

которое имеет два решения: одно – соответствующее минимуму , а другое – максимуму . Таким образом, последнее решение является оценкой для , полученной методом максимального правдоподобия. Подставив ее в (3.2.22), получим оценки для параметров и .

20. Оценка риска в модели ценообразования финансовых активов

Рассмотрим уравнение регрессии для модели Шарпа – Линтнера, записанное в следующем виде:

.

В соответствии с предположением 5 для этого уравнения , следовательно:

. (3.2.23)

Для уравнения регрессии модели Блэка:

получим то же выражение (3.2.23).

Риск, связанный с инвестированием в актив , оценивается исходя из подхода Марковитца дисперсией его доходности и складывается из двух частей: систематического, присущего рынку в целом, и несистематического, связанного непосредственно с активом. Выражение (3.2.23) показывает, что систематический риск измеряется величиной , определяемой дисперсией рыночного портфеля, а несистематический риск оценивается как 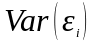. Таким образом, коэффициент бета актива имеет отношение к систематическому риску. В редких случаях, когда , т.е. 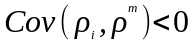, актив с отрицательной премией за риск используется для страхования от риска, связанного с рыночным портфелем.

Покажем далее на примере модели Шарпа – Линтнера (результаты для модели Блэка будут аналогичными), что несистематический риск может быть снижен с помощью диверсификации. Пусть инвестор формирует портфель , тогда его доходность будет . Для актива имеем:

.

Следовательно:

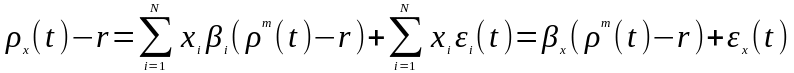
где .

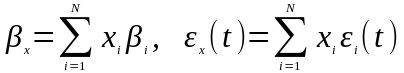Отсюда .

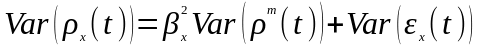Пусть . Тогда для несистематического риска диверсифицированного портфеля имеем:

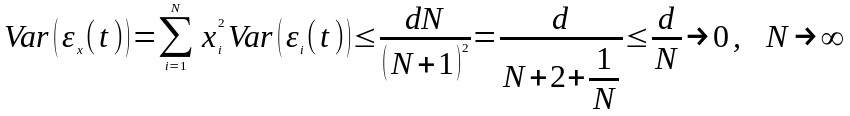
21. Однопродуктовая динамическая макроэкономическая модель

Исследование взаимосвязей элементов производства приводит к рассмотрению производствен­но-технологической интерпретации экономики.

Представим эти взаимосвязи в виде схемы на рис. 18.1.

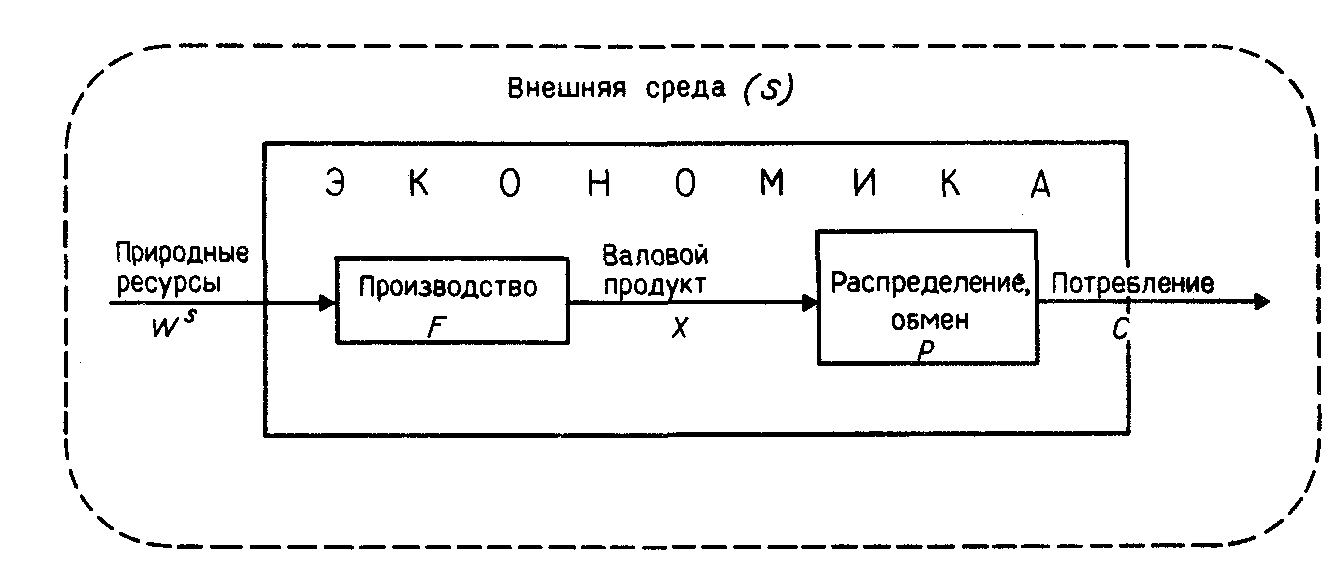
Рис. 18.1

На рис. 18.2 выделены факторы, характеризующие производство: труд ( ), средства труда (основные производственные фонды) ( ) и предметы труда (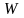 ). Последние включают, с одной стороны, элементы природы, или природные ресурсы ( ), и предметы труда ( ), возвращенные в производство как часть совокупного общественного продукта.

Результатом производственной деятельности является валовой продукт (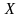 ), распределяемый в блоке на производственное потребление ( ), и конечный продукт ( ). В свою очередь, конечный продукт ( ) делится в блоке распределения на валовые капитальные вложения ( ) и непроизводственное потреб­ление ( ). Валовые капитальные вложения ( ) делятся на амортизационные отчисления ( ) и чистые капитальные вложения, идущие на расширение производственных фондов (блок ).

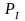Механизм воздействия чистых капитальных вложений на основные производственные фонды (ОПФ) сложен и при модели­ровании связан с определенными трудностями. Он составляет предмет самостоятельных экономико-математических исследований.

Представляет интерес изучение взаимосвязей между синтетическими показателями верхнего уровня экономической иерархии. Одним из подходов к решению данной проблемы является построение одно продуктовой макроэкономической модели.

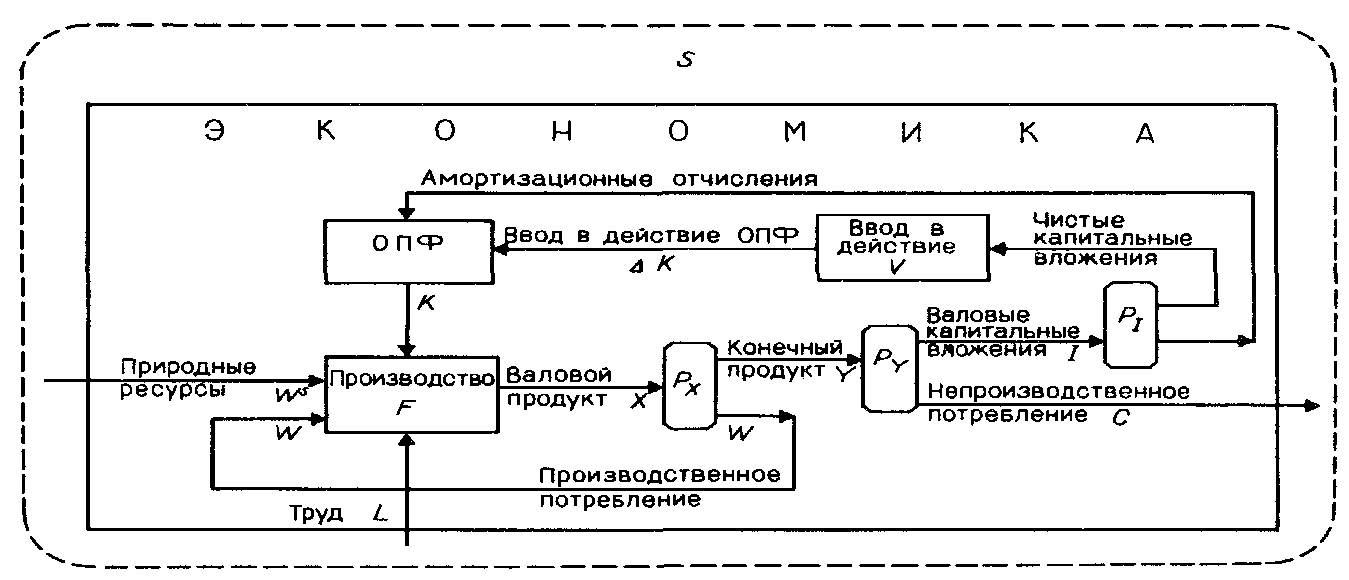
Рис. 18.2

Одно продуктовые макроэкономические модели — это модели, изучающие свойства и тенденции изменения взаимосвязанных агрегированных макроэкономических показателей, таких, как валовой продукт, конечный продукт, трудовые ресурсы, произ­водственные фонды, капитальные вложения, потребление и т. д. Рис. 2 помогает выявить эти взаимосвязи. Так, на макроуровне блок распределения показывает взаимосвязь между валовым продуктом , производственным потреблением и конечным продуктом :

(18.1)

Блок делит конечный продукт на две составляющие: валовые капитальные вложения и непроизводственное потребле­ние , т. е.

(18.2)

За счет капитальных вложений осуществляется ввод в действие основных производственных фондов. Однако формализация взаимосвязи «капитальные вложения — ввод в действие основных производственных фондов» сопряжена с определенными труднос­тями, одной из которых является учет распределенного запазды­вания прироста основных фондов от капитальных вложений. В экономико-математическом моделировании существует ряд подходов к описанию этой взаимосвязи.

В простейшей одно продуктовой модели делают предположение, что валовые инвестиции полностью расходуются на прирост основных производственных фондов в том же году и на амортизационные отчисления:

а) в дискретном варианте эта взаимосвязь имеет вид

, (18.3)

где — прирост основных производственных фондов в году ; — параметр модели; — амортизационные отчисления; — коэффициент амортизации; — основные производст­венные фонды в году ;

б) аналогом этого уравнения в непрерывном варианте является

. (18.3а)

Отсюда можно получить уравнение движения фондов:

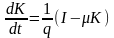. (18.3б)

Объединяя уравнения связи (1) - (3), получим однопродуктовую динамическую макромодель в дискретном варианте:

,

Если считать производственные затраты пропорциональны­ми выпуску продукции , т. е.

(18.4)

то дискретная однопродуктовая динамическая модель примет вид

,

или

а в непрерывном варианте — соответственно

.

В некоторых случаях используют упрощенные варианты однопродуктовой динамической модели.

Случай 1. Открытая однопродуктовая динамическая модель Леонтъева. Предполагают, что все валовые капитальные вложения идут на ввод в действие новых основных производственных фондов (основные фонды не изнашиваются). Считая, что прирост выпуска продукции 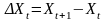пропорционален капитальным вложениям, т. е.

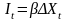(18.5)

из уравнений (18.1), (18.2), учитывая (18.4), (18.5), получим однопродуктовую открытую динамическую модель Леонтьева:

.

В непрерывном варианте однопродуктовая динамическая мак­ромодель Леонтьева имеет вид

. (18.6)

С математической точки зрения эта модель представляет собой линейное неоднородное дифференциальное уравнение.

Случай 2. Замкнутая однопродуктовая модель Леонтьева. Предполагают, что непроизводственное потребление 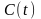идет полностью на восстановление рабочей силы . Тогда, введя норму потребления , получим

. (18.7)

Далее, если считать, что затраты труда пропорциональны выпуску продукции, то

, (18.8)

где 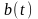- норма трудоемкости.

Подставляя (18.7) в (18.6) с учетом (18.8), получим «замкнутую по потреблению» модель расширенного воспроизводства

,

которая описывается однородным дифференциальным уравнением

(18.9)

где

.

Тогда развитие экономики определяется решением уравнения (18.9):

.

Случай 3. Предполагают, что непроизводственное потребление является известной функцией времени. Тогда закон развития экономики определим из модели (6), которая с математической точки зрения является неоднородным дифференциальным уравнением вида

,

где , с решением

.

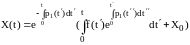Итак, можно сделать следующий вывод. Выделение из конечно­го продукта накапливаемой части 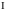приводит к рассмотрению динамических моделей и применению для исследования в качестве математического аппарата теории дифференциальных (в непрерывном случае) и конечно-разностных уравнений (в многошаговом варианте).

22. Двухпродуктовая динамическая макроэкономическая модель

Предположим, что экономика представлена двумя отраслями народного хозяйства, каждая из которых выпускает валовую продукцию , и затрачивает на воспроизводство труд, средства труда и предметы труда. Валовой продукт каждой отрасли распределяется в блоках и (рис. 18.3) соответствен­но на конечный продукт , отраслей и производственное потребление , :

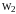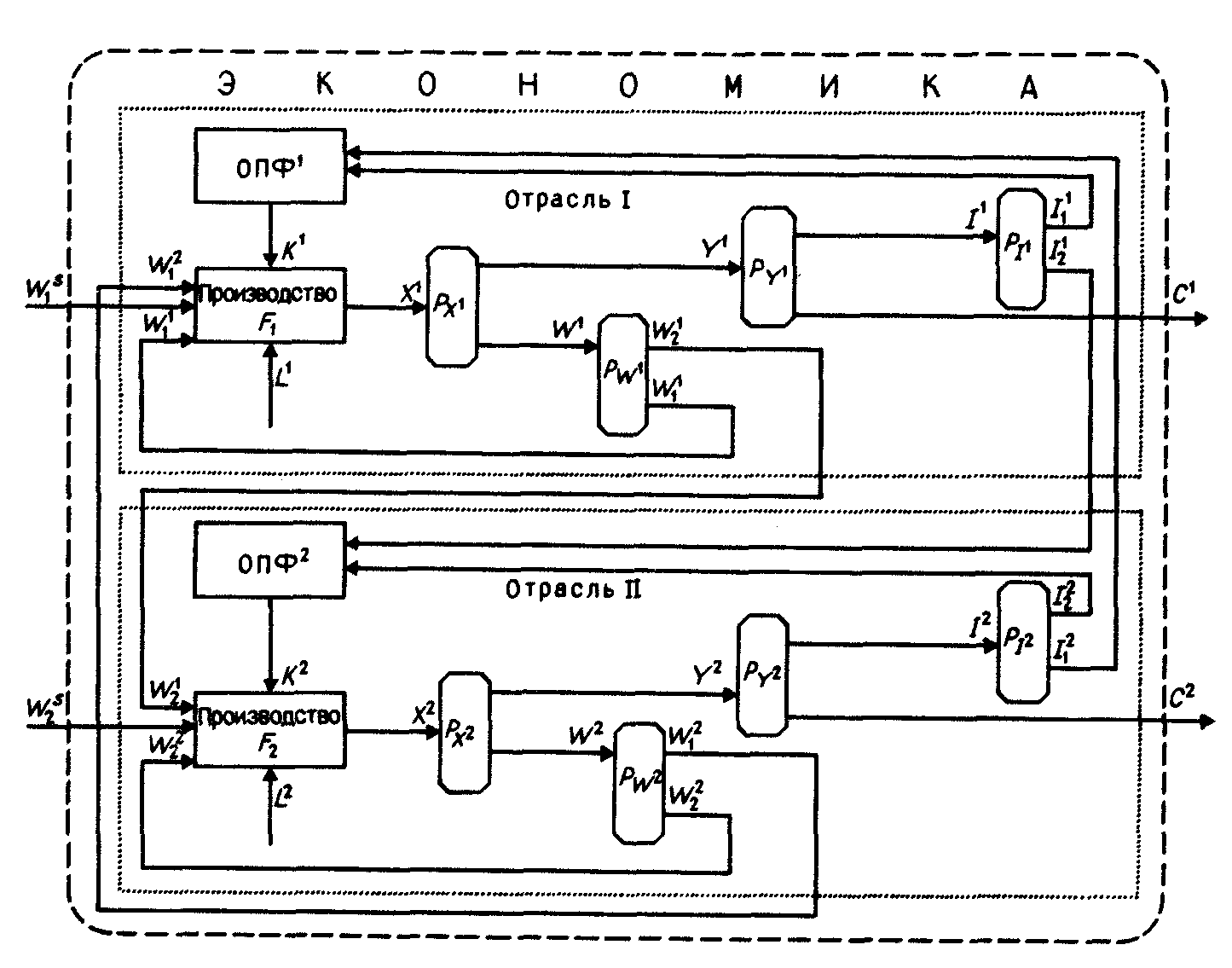
Рис. 18.3

Однако в двухпродуктовой модели промежуточный продукт ( ) расходуется на воспроизводство валового продукта не только своей отрасли, но и другой. На рис. 3 распределение промежуточного продукта осуществляется в блоках и :

Если предположить, что межотраслевые потоки ( ) из -й отрасли в -ю отрасль пропорциональны объему валовой продукции -й отрасли:

где —норма затрат продукции -й отрасли на воспроизводство единицы продукции -й отрасли,— то распределение валовой продукции отраслей можно представить в виде

(18.10)

Из схемы на рис. 3 видно, что блоки и участвуют в межотраслевом обмене промежуточного продукта и образуют систему межотраслевых связей.

Дальнейшее деление конечного продукта , отраслей I и II соответственно на валовые капитальные вложения , и непроиз­водственное потребление 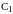, осуществляется в блоках и :

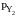(18.11)

что приводит к вводу в балансовое уравнение составляющих , связь которых с валовым продуктом выражена конечно-разностными (в дискретном варианте) или дифференциальными (в непрерывном варианте) уравнени

В двухпродуктовой модели в простейшем варианте будем считать, что все валовые капитальные вложения идут на развитие экономики (амортизационные отчисления в этом случае не учитываем). Тогда расход валовых капитальных вложений , каждой отрасли на увеличение основных фондов осуществ­ляется соответственно в блоках и :

(18.12)

В простейшей динамической модели считаем, что поток валовых капитальных вложений 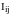( ) из -й отрасли в -ю пропорционален приросту валовой продукции -й отрасли:

(18.13)

Подставляя в (10) формулы (11) – (13), получим открытую двухпродуктовую модель в дискретном варианте:

(18.14)

В непрерывном варианте модель (14) примет вид

Задавая в базисном году величину и предполагая известными потребления во времени и , видим, что задача развития экономики, заданной двумя отраслями, сводится к системе линейных неоднородных уравнений.

С математической точки зрения эта задача является задачей Коши для обыкновенных дифференциальных уравнений.

23. Моделирование запаздывания при освоении капитальных вложений

При идентификации процессов на макроуровне одним из главных вопросов является формирование взаимосвязей факторов с учетом запаздывания. Так, например, цепочка «капитальные вложения - ввод в действие основных производственных фондов» относится к числу таких взаимосвязей.

Имеется два подхода при моделировании запаздывания в процессе освоения капитальных вложений. Первый из них предполагает наличие промежутка времени , по прошествии которого капиталовложения превращаются в основные фонды. В этом случае можно считать, что изменение основных фондов в момент происходит за счет инвестиций, выделенных в момент . Тогда модель прироста основных фондов в непрерывном варианте принимает вид

(Здесь параметр )

Это уравнение представляет собой уравнение с запаздыванием, или, как принято в теории дифференциальных уравнений, уравнение с отклоняющимся аргументом. Величина называется параметром запаздывания и определяет значение лага, т.е. времени, необходимого на освоение инвестиций.

Наряду с данной моделью в настоящее время используется подход к моделированию запаздывания, основанный на введении так называемого распределенного лага. При этом предполагается, что инвестиции, выделяемые на развитие основных фондов, осваиваются постепенно. Это значит, что если в момент времени выделены инвестиции , то в момент времени будет освоена доля инвестиций. Если теперь взять все моменты времени , то получим следующую формулу для освоения кап. вложений (инвестиций) (или ввода в действие основных фондов ) в момент времени :

. (18.15)

В случае дискретной (многошаговой) модели, когда инвестиции образуются в моменты времени 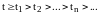, формулу (18.15) можно переписать следующим образом:

. (18.16)

Если доля инвестиций, образованных в момент времени и вводимых в действие в момент времени , зависит лишь от промежутка времени освоения , то говорят о стационарности процесса ввода инвестиций в действие. В этом случае функция будет, очевидно, зависеть лишь от и, следовательно, равна . Формула (18.15) тогда примет вид

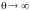Введем новую переменную . Если , то , а если , то . Тогда выражение для примет вид

. (18.17)

Функция является важной характеристикой процесса освоения инвестиций (ввода в действие капиталовложений). Одним из предположений о ее поведении, которое может быть принято, является предположение о монотонном убывании , т. е. доля вводимых в заданный момент времени инвестиций, выделенных в момент времени , будет тем меньше, чем больше промежуток времени . При моделировании инвестиционного лага используются различные способы задания функции . Зададим ее в виде

. (18.18)

Функция должна удовлетворять следующим условиям

А) При доля вводимых инвестиций должна убывать к нулю, иначе говоря, должно иметь место соотношение .

Б) Условие нормировки

(18.19)

Очевидно, что рассматриваемая функция распределения лага перечисленным условиям удовлетворяет, так как

.

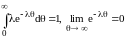Получим теперь уравнение для скорости ввода капитальных вложений . Для этого вычислим производную левой и правой частей соотношения (18.17). Вычисляя производную правой части по правилу дифференцирования интеграла по параметру, получим

. (18.20)

Подставим соотношение в равенство (18.20). Получившийся при этом интеграл можно вычислить по частям:

или

. (18.21)

Для экспоненциального закона запаздывания уравнение (18.21) упрощается. В этом случае . Поэтому уравнение (18.21) можно переписать в виде

.

Но с учетом (18.17) последнее слагаемое будет равно , поэтому окончательно получим

. (18.22)

Как видно из соотношения (18.22), в случае экспоненциального закона запаздывания объем вводимых в действие капитальных вложений может быть найден с помощью решения обыкновенного дифференциального уравнения (18.22). При этом необходимо задать значение 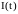и начальное значение 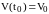. После этого определяется как решение задачи Коши. Теперь модель роста основных фондов будет выглядеть так:

(18.23)

Таким образом, в случае экспоненциального распределения лага основные производственные фонды отрасли могут быть найдены из системы дифференциальных уравнений (18.23).

Зависимости типа (18.22), (18.23) могут быть получены и в дис­кретной модели ввода в действие основных фондов (18.16). Аналогом соотношения (18) является при этом функция

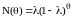. (18.24)

которая, как нетрудно проверить, удовлетворяет условию (ср. с (18.19))

. (здесь ).

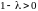Рассмотрим соотношение (18.16). Предположим, как и в не­прерывном случае, что фигурирующая в нем функция 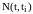зависит лишь от разности . Обозначая эту разность через и используя для формулу (18.24), перепишем соотношение (18.17) в виде

. (18.25)

Последнее равенство можно записать в виде

. (18.26)

Второе из слагаемых в правой части, если обозначить , можно представить в виде

. (18.27)

Сравнивая выражение (18.27) с (18.25), легко заметить, что оно равно

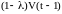. Учитывая это соотношение, формула (18.26) примет вид

.

Последнее уравнение позволяет определить, каким будет ввод в действие капитальных вложений , если известно, какими были сами капитальные вложения. Оно является дискретным аналогом уравнения (18.22).

24. Однопродуктовая оптимизационная динамическая макроэкономическая модель

Развитие экономики подчинено целостной системе экономических законов, отражающих глубинные. внутренние. существенные ее связи.

В конечном итоге содержание критерия развития экономики сводится к определению максимального «съема» с экономики, наибольшей эффективности общественного производства

В рассматриваемой нами оптимизационной модели в качестве критерия оптимальности предполагается максимизировать дисконтированную сумму потребления, создаваемого в течение всего срока планирования:

, (18.28)

где - непроизводственное потребление. - функция дисконтирования, отражающая меру предпочтения потребления в данный момент относительно потребления того же продукта в последующие моменты.

Итак, если стоит задача оптимального развития экономики, то ее можно сформулировать следующим образом: определить такой вариант выпуска продукции 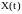и такое непроизводственное потребление . которые обеспечат наибольшее интегральное дисконтированное потребление.

Модель примет следующий вид.

Для экономики, распределение продукции которой определено дифференциальным уравнением связи

,

выпуск продукции ограничен производственными возможностями 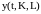(здесь - производственная функция) :

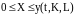
а рост производственных фондов ограничен снизу:

.

Найти такой вариант развития, который обеспечивает максимум функционала (18.28).

Итак, однопродуктовая модель, рассмотренная в данном параграфе, учитывает не только динамику, но и цель развития экономики.

Количественное определение оптимального варианта развития с помощью этой модели связано с использованием аппарата теории оптимального управления.

25. Многоотраслевая оптимизационная динамическая модель

Дезагрегирование динамической однопродуктовой макроэкономической модели приводит к рассмотрению развития много­отраслевой экономики.

Рассмотрим экономику, представленную отраслями, каждая из которых идентифицируется отраслевым уравнением воспроизводства основных фондов в предположении, что валовые капитальные вложения полностью расходуются без учета запаздывания на прирост основных производственных фондов и на амортизационные отчисления:

, (здесь параметр ) (18.29)

где - интенсивность валовых капитальных вложений - й отрас­ли; - коэффициент амортизационных отчислений - й отрасли; - основные фонды — ой отрасли.

При известном уровне основных производственных фондов в базисном году

(18.30)

производственные возможности отраслей ограничены производ­ственной функцией отрасли

(18.31)

где – интенсивность валовых инвестиций -й отрасли; – трудовые ресурсы -й отрасли.

Межотраслевые связи представлены балансовыми соотношениями

, (18.32)

, (18.ё33)

где - интенсивность конечного продукта -й отрасли; 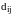- структурные коэффициенты основных производственных фондов; 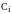- интенсивность производственного потребления -й отрасли.

Трудовые ресурсы отраслей ограничены неравенством

. (18.34)

Кроме того, из экономических соображений известно, что

. (18.35)

В качестве исходной информации задаются начальные значения основных производственных фондов ,коэффициенты амортизации отраслей , матрица коэффициентов прямых затрат , матрица структуры фондов , суммарные трудовые ресурсы , определяемые демографическим прогнозом, произ­водственные функции отраслей .

Необходимо найти модель процесса , оптимального в смысле

где - множество процессов (планов), определяемых условиями (18.29) — ( 18.35); 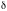- коэффициент дисконтирования; - функция полезности, вогнутая с положительным градиентом.

Введение нелинейных производственных функций в межотраслевой баланс позволяет учесть возможность взаимного замещения труда и фондов в отраслях и зависимость производительности труда от фондовооруженности (в нелинейных моделях производительность труда считается заданной функцией времени).

Рассмотренная нелинейная оптимизационная модель развития многоотраслевой экономики также является задачей, решаемой с помощью теории оптимального управления.

-------------------Возможно не будет, уточнить---------------------------

26. Модель оптимальных управляемых процессов. Математические понятия

27. Модель оптимальных управляемых процессов. Общая задача оптимизации

28. Задача оптимизации управляемых процессов

29. Примеры 1,2 задач оптимального управления

30. Примеры 3,4 задач оптимального управления

31. Метод Лагранжа для многошаговых процессов управления

32. Примеры применимости условий оптимальности. Пример 1 (календарное планирование поставки продукции).

33. Примеры применимости условий оптимальности. Пример 2 (оптимальное потребление в однопродуктовой макромодели).

-----------------------На практику-----------------------------------

34. Теория риска. Модель индивидуальных потерь.

35. Теория риска. Модели наступления страховых случаев.

36. Теория риска. Модель индивидуального риска.

37. Теория риска. Модель коллективного риска.

+Вопросы по теме рядов