1.Линейные временные ряды
Многие финансовые
данные рассматриваются в форме временных
рядов, т.е.
последовательности наблюдений одной
и той же случайной переменной: стоимости
акций, курса валюты, объема торгов на
бирже и т.д. Будем обозначать такую
последовательность как
.
Реализации
этой последовательности, т.е. имеющиеся
к моменту времени
наблюдения будем обозначать следующим
образом:
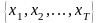или
Последовательность
называется строго
стационарной,
если совместное распределение
аналогично совместному распределению
,
или
для любых
положительных целых чисел
и
.
Строгую стационарность довольно сложно
проверить эмпирически, поэтому на
практике чаще подразумевают слабую
стационарность.
Последовательность называется слабо стационарной, если ее первый и второй моменты конечны и не зависят от времени, т.е.
для любого целого
.
Если последовательность является строго стационарной с конечными первым и вторым моментами, то она по определению слабо стационарна. Обратное утверждение, вообще говоря, не верно. Однако, если последовательность нормально распределена, то в этом случае слабая стационарность эквивалентна сильной.
Далее, говоря, что последовательность является стационарной, будем подразумевать слабую стационарность.
Ковариация
стационарной последовательности
называется автоковариацией
с лагом
.
Она обладает следующими свойствами:
Корреляция между
и
называется автокорреляцией
с лагом
.
Для стационарной последовательности
автокорреляция, как и автоковариация,
зависит только от
:
.
Имеем следующие свойства автокорреляции:
Важную роль при
моделировании временных рядов играет
так называемый белый
шум
последовательность независимых одинаково
распределенных гауссовских случайных
величин
.
Временной ряд является линейным, если он представим в виде следующей линейной комбинации:
,
где
среднее стационарного временного ряда
,
белый шум,
.
Коэффициенты
называют
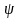-весами
временного ряда
.
Поскольку стационарный временной ряд, то мы имеем:
2.Авторегрессионная модель
Авторегрессионная
модель порядка
отражает линейную зависимость
от предыдущих
значений искомой случайной величины:
.
Имеем следующие примеры авторегрессионной
модели различного порядка:
(3.5.1)
Будем считать авторегрессионные модели (3.5.1) стационарными (т.е. временной ряд , описываемый этими моделями является стационарным).
Авторегрессионная модель
Модель авторегрессии
первого порядка отражает линейную
зависимость
только от одного прошлого значения
.
Имеем:
,
откуда, с учетом
того, что
,
получаем:
,
где
Далее, используя
равенство
и уравнения
для
,
получаем:
(3.5.2)
Отсюда следует, что
Тогда из (3.5.2) получаем:
Из последнего
выражения следует,что
.
Это неравенство является необходимым
и достаточным условием стационарности
модели
.
Легко заметить, что
Тогда
и получаем следующие формулы для автоковариации модели :
Из последних равенств легко считаются автокорреляции :
при этом
.
Эта формула показывает, что автокорреляционная
функция модели
экспоненциально убывает, поскольку
.