4.Авторегрессионная модель скользящего среднего

Авторегрессионная модель скользящего среднего порядка является комбинацией двух моделей: авторегрессионной и скользящего среднего . Она имеет следующий вид:

.

Используя оператор сдвига назад, получим следующую форму записи :

.

Обозначим через и полиномы оператора , т.е.:

тогда модель можно записать так:

.

Разделим полиномы и один на другой и получим:

По определению .

Полученные результаты деления полиномов и позволяют получить весьма важные представления модели в виде авторегрессионной модели и модели скользящего среднего.

Так, как результат деления на получаем следующее - представление для :

,

достаточным условием которого является то, что все нули полинома по модулю больше единицы.

Аналогично, как результат деления на получаем следующее - представление для :

.

Остановимся подробнее на свойствах модели

.

Среднее для этой модели находится легко:

,

откуда, с учетом стационарности , получаем:

.

Этот результат совпадает со значением среднего модели .

Далее положим для простоты, что . Найдем вариацию для модели . Для этого прежде всего посчитаем математическое ожидание произведения :

.

Теперь находим вариацию для :

.

Отсюда, с учетом стационарности и получаем:

, где .

Последнее условие, являющееся условием стационарности , совпадает с условием стационарности .

Чтобы найти автоковариацию модели , умножим обе ее части на :

.

Для находим:

.

Для :

.

Зная автоковариацию и вариацию, легко найти автокорреляцию:

Заметим, что значения автоковариации и автокорреляции для при совпадают с соответствующими значениями автоковариации и автокорреляции для , в то время как при эти значения отличаются на величину 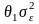и 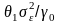соответственно.

Отметим еще одно важное свойство, присущее моделям любого порядка. Характеристические корни являются и характеристическими корнями . Если

,

где  характеристические корни , то, как и в случае , модель является стационарной.

5.Моделирование с помощью линейных временных рядов.

При построении модели, описывающей динамику биржевых индексов, цен акций или облигаций, курса валют и т.д. на основе имеющихся эмпирических данных необходимо осуществление следующей последовательности действий:

1. определение порядка модели, который делает модель наиболее адекватной для прогнозирования;

2. оценка параметров модели, т.е. ее коэффициентов;

3. оценка адекватности построенной модели.

6.Моделирование с помощью ar(p) и ма(q) Моделирование с помощью

Наиболее распространенным способом определения порядка модели является способ, основанный на использовании так называемой частной автокорреляционной функции.

Рассмотрим последовательность авторегрессионных моделей возрастающего порядка:

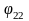
Коэффициенты называют частной автокорреляционной функцией. Так,  частная автокорреляционная функция первого порядка,  частная автокорреляционная функция второго порядка и т.д.

Частная автокорреляционная функция первого порядка показывает, какую часть в величину вносит . Соответственно, показывает вклад в величину и т.д. Следовательно, для модели частная автокорреляционная функция порядка , т.е. , должна быть отлична от нуля, иначе порядок модели можно снизить до . В то же время, частная автокорреляционная функция порядка , т.е. , должна быть равна нулю, иначе порядок модели можно увеличить до .

На практике величины частной автокорреляционной функции заранее не известны и рассчитываются на основе имеющихся реализаций с использованием, например, метода наименьших квадратов. Построенные оценки , и т.д. называются выборочные частные автокорреляционные функции. Для них справедливы следующие утверждения:

сходится к при ;

для всех .

В соответствии с найденным значением , строим модель:

.

В случае адекватности построенной модели ряд остаточных членов , где

,

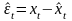является белым шумом. Для проверки гипотез:

где  автокорреляция с лагом ряда применяют так называемую статистику Льюнга-Бокса:

,

которая ассимптотически имеет распределение . Здесь вместо автокорреляций используются выборочные автокорреляции . В качестве параметра можно брать любое целое число, большее порядка модели.