Авторегрессионная модель
Для модели
,
имеем:
,
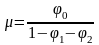где
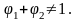
Далее, используя методику, изложенную выше, получаем следующие формулы для автоковариации и автокорреляции:
.
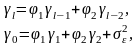
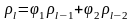С целью компактности
изложения введем оператор сдвига назад
,
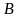действующий на числовых последовательностях
:
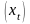Далее имеем:
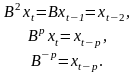
Отметим следующие свойства оператора :
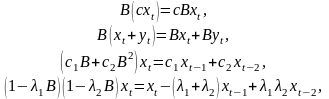
где
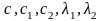
константы.
Используя оператор , можно переписать модель следующим образом:
,
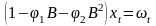где
.
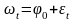
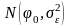(3.5.3)
Обозначим через
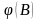полином оператора
,
т.е.:
,
тогда получаем:
.
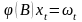Рассмотрим теперь
вопрос об обратимости модели
,
т.е. нахождении
по значению
.
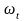Для любых
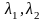справедливо равенство (свойство оператора
):
.
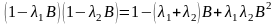Возьмем такие, что:
т.е. являющиеся корнями квадратного уравнения
.
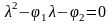Иными словами
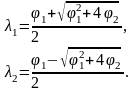
Тогда получим, что
.
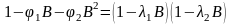С учетом полученного равенства уравнение (3.5.3) можно переписать следующим образом:
.
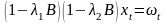Отсюда получаем:
.
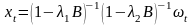Найдем
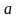и
,
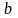такие, что
.
Поскольку
,
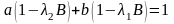то получаем:
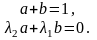
Решая систему уравнений относительно и , получаем:
Следовательно,
.
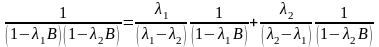Тогда будет выражаться следующим образом:
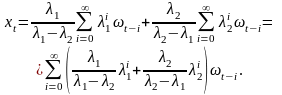(3.5.4)
Отметим далее, что не всякая модель является обратимой. Для представления модели в виде (3.5.4) необходимо, чтобы удовлетворяли следующему условию:
.
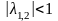В этом случае модель будет стационарной.
Авторегрессионная модель
Для модели
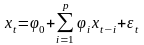
имеем:
,
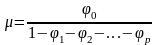где
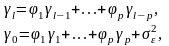
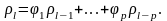
Используя оператор , можно переписать авторегрессионную модель следующим образом:
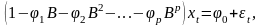
или, обозначив полином оператора :
,
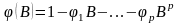получаем:
,
где
.
Используя тот же
метод, что и для
,
рассмотрим вопрос об обратимости модели
.
Для этого необходимо найти характеристические
корни
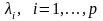для разложения полинома:
.
Если
,
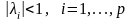то находим стационарное решение для
:
.
Характеристические корни являются решением уравнения:
.
Необходимо найти разложение:
.
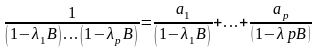Умножая обе части
на
,
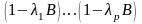получаем:
.
Отсюда:
.
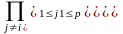Тогда получаем аналог разложения (3.5.4) для модели :
.
(3.5.5)
3.Модель скользящего среднего
Модели скользящего
среднего
описывают эволюцию
как зависимость от
прошлых значений белого шума
:
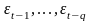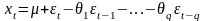
или, используя оператор сдвига :
.
Обозначим через
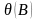полином оператора
,
т.е.:
,
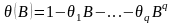тогда модель можно записать так:
.
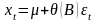Приведем примеры моделей первого и второго порядка:
Модель любого порядка всегда стационарна, так как является линейной комбинацией стационарного белого шума.
Среднее,
автоковариация и автокорреляция для
модели
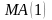считается достаточно просто:
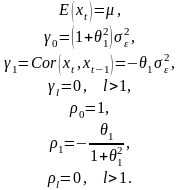
Аналогичным
образом для модели
получаем:
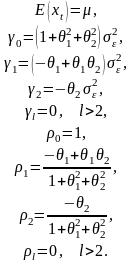
Соответственно, для имеем:
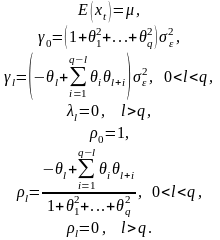
Заметим, что
автоковариация и автокорреляция с
лагом, большим порядка модели скользящего
среднего, т.е.
,
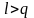равна нулю. Это свойство оказывается
очень полезным при идентификации порядка
модели, строящейся на основе имеющихся
эмпирических данных о поведении
последовательности
.
Уравнения (3.5.4) и
(3.5.5) показывают, что всякая стационарная
модель
допускает представления в виде модели
:
.
Верно и обратное:
модель
допускает представления в виде модели
:
с соответствующими
коэффициентами
