
- •Вопросы для зачета по математической экономики (2 часть)
- •Дюрация и показатель выпуклости портфеля. Средняя продолжительность платежей – дюрация
- •Вероятностная модель финансового рынка
- •Модель Шарпа – Линтнера
- •1.Линейные временные ряды
- •2.Авторегрессионная модель
- •Авторегрессионная модель
- •Авторегрессионная модель
- •Авторегрессионная модель
- •3.Модель скользящего среднего
- •4.Авторегрессионная модель скользящего среднего
- •5.Моделирование с помощью линейных временных рядов.
- •6.Моделирование с помощью ar(p) и ма(q) Моделирование с помощью
- •Моделирование с помощью
- •7.Моделирование с помощью arma(p,q)
- •8.Сезонные модели
- •Далее рассмотрим следующий ряд разностей, теперь уже четвертого порядка:
- •1.Основные понятия
- •2.Определение стоимости опциона на момент исполнения
- •3.Создание безрисковых портфелей с помощью call-опционов
- •4.Создание безрисковых портфелей с помощью put-опционов
- •5.Создание безрисковых портфелей с помощью put-опционов
4.Создание безрисковых портфелей с помощью put-опционов
Пусть цена актива равна 60 д.е., такова же и цена исполнения опциона на продажу. Срок действия опциона европейского типа один месяц. Предположим, что к концу месяца с вероятностью 1/2 цена актива либо поднимется на 15 д.е., либо опустится на столько же. В первом случае опцион непосредственно перед исполнением будет стоить 15 д.е., во втором не будет стоить ничего. Поэтому в первом случае продавец опциона должен заплатить держателю опциона 15 д.е., во втором случае он не должен ничего платить. Так как размах колебаний цен актива равен 30 д.е. и ровно в два раза превосходит колебания стоимости опциона перед исполнением, то для создания безрискового портфеля держатель актива должен купить 2 опциона на продажу. Проверим, что портфель из актива и этих двух опционов действительно безрисковый.
В самом деле, в рамках рассматриваемой модели к концу месяца цена актива будет либо 75 д.е., либо 45 д.е. В первом случае владелец портфеля ничего не будет делать с купленными им опционами на продажу, во втором случае продавец опционов выплатит ему по 15 д.е. за опцион. В обоих случаях к концу месяца портфель будет стоить 75 д.е. независимо от цены актива. Это и означает его безрисковость.
Теперь перейдем непосредственно к определению цены опциона. Пусть банковская безрисковая ставка равна 10%. Так как портфель безрисковый, то его современную стоимость найдем, дисконтируя его стоимость в конце месяца по безрисковой ставке. Итак, его современная стоимость равна 75/(1+0,1) = 68,2 д.е. Но сейчас актив стоит 60 д.е. и поэтому два опциона вместе стоят 68,2 – 60 = 8,2 д.е. Следовательно, один опцион стоит 4,1 д.е. За такую цену оба опциона и должны быть куплены.
Проследим детально, как в § 13.4, за капиталом покупателя опционов. Сначала у него был только актив стоимостью 60 д.е. Потом он купил два опциона, каждый по 4,1 д.е. Теперь у него денег – 8,2 д.е. — долг за купленные опционы, актив стоимостью 60 д.е. и два опциона, являющиеся фактически тоже активами, цена этих активов 8,2 д.е. Прежний актив и эти два опциона вместе образуют безрисковый портфель стоимостью 68,2 д.е. К концу месяца – 8,2 д.е. уменьшатся по безрисковой ставке до -8,2(1+0,1) = -9 д.е., стоимость безрискового портфеля возрастет по безрисковой ставке до 75 д.е., всего у покупателя будет 75 – 9 = 66 д.е. — в точности как если бы его актив был безрисковым и его стоимость возросла бы по безрисковой ставке до 60 (1+0,1) = = 66 д.е.! Умелое хеджирование, как и в п. 13.4, полностью оградило покупателя от риска.
5.Создание безрисковых портфелей с помощью put-опционов
С помощью опциона на покупку можно застраховаться от излишне высокого повышения цены на интересующий актив и обеспечить его приобретение по сегодняшней цене. Это делается следующим образом.
Купим
опцион на покупку этого актива по цене
исполнения
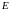 и
одновременно денежную сумму величиной
и
одновременно денежную сумму величиной
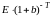 ,
вложим
в банк по безрисковой ставке
,
вложим
в банк по безрисковой ставке
 .
К
моменту исполнения опциона, т.е. через
время
.
К
моменту исполнения опциона, т.е. через
время
 ,
эта
сумма возрастет
до
.
Если
цена актива к этому моменту не превысит
,
то
купим актив; иначе купим актив с помощью
имеющегося у нас опциона на покупку.
,
эта
сумма возрастет
до
.
Если
цена актива к этому моменту не превысит
,
то
купим актив; иначе купим актив с помощью
имеющегося у нас опциона на покупку.
Между стоимостями опционов на покупку и на продажу есть связь, известная как теорема паритета опционов.
Пусть
 —
стоимости соответственно опциона на
покупку
и опциона на продажу и
—
стоимости соответственно опциона на
покупку
и опциона на продажу и
 —
цена актива в момент продажи-покупки
опционов и соответственно цена исполнения.
Тогда
—
цена актива в момент продажи-покупки
опционов и соответственно цена исполнения.
Тогда
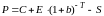 , (13.2)
, (13.2)
где — безрисковая ставка, — время опциона.
Для доказательства этой формулы проведем два мысленных эксперимента.
1.
Приобретем актив по цене
и опцион на продажу с ценой
исполнения
и
стоимостью
 ,
затратив
всего
,
затратив
всего
 .
Если
цена актива в момент исполнения опциона
превысит
,
то
актив сохраним, в противном случае актив
продадим по
цене Е.
.
Если
цена актива в момент исполнения опциона
превысит
,
то
актив сохраним, в противном случае актив
продадим по
цене Е.
2.
Купим опцион на покупку этого актива с
ценой исполнения
и
стоимостью
и
одновременно вложим по безрисковой
ставке
денежную
сумму величиной
,
всего
затратим
 ;
к
моменту
исполнения опциона,
т.е. через время
,
эта
сумма возрастет по безрисковой ставке
до
.
Если
цена актива к этому моменту не превысит
,
то
купим актив; иначе купим актив с помощью
имеющегося
у нас опциона на покупку.
;
к
моменту
исполнения опциона,
т.е. через время
,
эта
сумма возрастет по безрисковой ставке
до
.
Если
цена актива к этому моменту не превысит
,
то
купим актив; иначе купим актив с помощью
имеющегося
у нас опциона на покупку.
В
рамках рассматриваемой модели оба
эксперимента дают в
конце один результат: если цена актива
к моменту исполнения
опциона превысит
,
то
будем
иметь актив, иначе — денежную
сумму
.
Следовательно,
и в начале этих экспериментов
наш капитал должен быть одинаковым,
т.е. должно быть
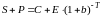 ,
откуда
и следует формула (13.2). Если
цена исполнения опционов совпадает с
сегодняшней рыночной
ценой актива, то опцион на покупку дороже
опциона
на продажу.
,
откуда
и следует формула (13.2). Если
цена исполнения опционов совпадает с
сегодняшней рыночной
ценой актива, то опцион на покупку дороже
опциона
на продажу.
1
2 См., например, Шарп У.Ф., Александер Г.Дж., Бэйли Дж.В. Инвестиции. — М.: ИНФРА-М, 1997. — с. 207-218.
3
