12.6. Невластиві інтеграли по області

12.6.1. Основні поняття

Інтеграли по області називають невластивими, якщо область інтегрування D необмежена або підінтегральна функція необмежена в деяких точках М області інтегрування. Невластиві інтеграли по області можуть бути збіжними або розбіжними.

Випадок нескінченної області. Якщо функція неперервна в нескінченій області D, то розглядають

, (1)

де D_n – обмежена область така, що і , тобто D_n розширюється за довільним законом і містить довільну точку область D.

Якщо границя правої частини рівності (1) існує і не залежить від вибору області D_n, то відповідний невластивий інтеграл по області D називається збіжним. Якщо ця границя не існує або дорівнює нескінченності, то невластивий інтеграл називають розбіжним.

Якщо підінтегральна функція невід’ємна в області D, то для збіжності невластивого інтеграла необхідно і достатньо, щоб границя правої частини рівності (1) існувала хоча би для одного вибору областей D_n.

Випадок розривної (необмеженої) функції. Якщо функція неперервна в замкненій обмеженої області D за виключенням точки М₀, то розглядають

, (2)

де – область, яка одержується із області D шляхом видалення області діаметром , яка містить точку М₀.

Якщо границя правої частини (2) існує і не залежить від виду видалених областей діаметром , то відповідний невластивий інтеграл називається збіжним, в протилежному випадку – розбіжним.

Якщо , то границя в (2) не залежить від виду видаленої області. В цьому випадку найчастіше видаляють окіл радіуса  точки М₀.

Якщо в області інтегрування підінтегральна функція має розриви другого роду (стає необмеженою) на деякій лінії L або поверхні S, то ця особливість видаляється із області інтегрування, а потім видалена частина стягується до особливості.

Приклад 11.Дослідити збіжність інтеграла , де область D – площина хОу.

Розв’язання. Заданий інтеграл є невластивим подвійним інтегралом по необмеженій області D, підінтегральна функція невід’ємна. Позначимо через D_R – круг радіуса R з центром в початку координат. Тоді рівність (1) прийме вигляд:

.

Обчислимо подвійний інтеграл по області D_R переходом до полярної системи координат:

.

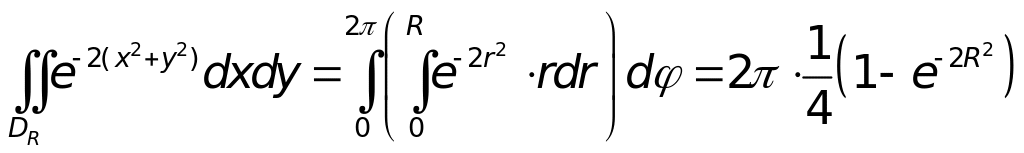Отже, .

Відповідь: невластивий інтеграл – збіжний і дорівнює .

Приклад 12. Дослідити збіжність інтеграла

.

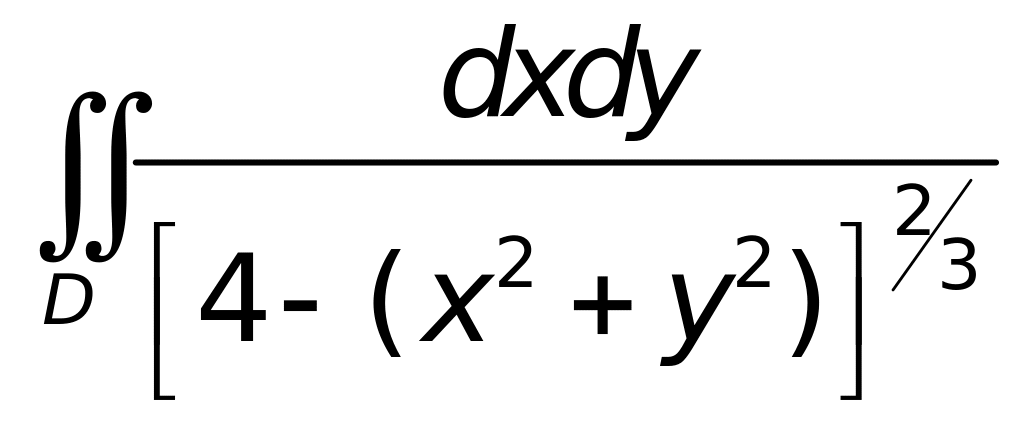Розв’язання. Задано невластивий подвійний інтеграл по обмеженій області від функції, яка необмежена на колі

х² + у² = 4 і невід’ємна.

Позначимо через круг радіуса R = 2 – з центром в початку координат. Тоді за формулою (2) одержимо:

.

Обчислимо подвійний інтервал по області переходом до полярних координат:

Заданий інтеграл дорівнює

,

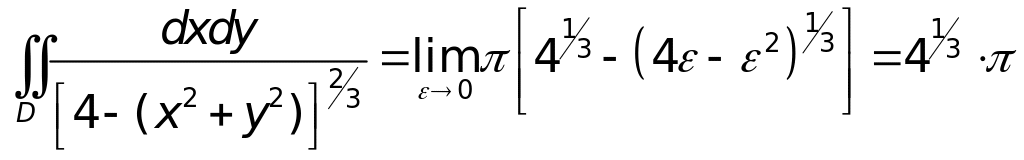тому він збіжний.

Зауваження:

1. Якщо підінтегральна функція і , то невластивий інтеграл по області називають абсолютно збіжним.

Для обчислення абсолютно збіжного інтеграла по області межі інтегралів можна визначати у будь-якій системі координат.

Якщо інтеграл по області абсолютно не збігається, то заміна змінних і переставлення порядку інтегрування потребують спеціального дослідження.

2. При дослідженні збіжності невластивих інтегралів по області часто застосовують порівняльні ознаки. Наприклад, якщо D є площиною, то для збіжності інтеграла істотно лише поведінка для великих , тому потрібно використовувати інтеграл , який збігається р > 2 і розбігається при р < 2.

Аналогічно в тривимірному просторі інтеграл від на нескінченності збігається лише при р > 3.

При досліджені невластивих інтегралів по області від функції, яка необмежена в ізольованій точці М₀ області D часто використовують порівняння з інтегралами на площині та в просторі.

Перший із вказаних інтегралів збігається при р < 2, а другий – при р < 3.

Якщо особливості підінтегральної функції не ізольовані, то умову збіжності часто вдається одержати шляхом вибору такої системи координат, в якій координатні лінії проходять вздовж особливості.

1.Обчислити інтеграли:

а) ; б) ;

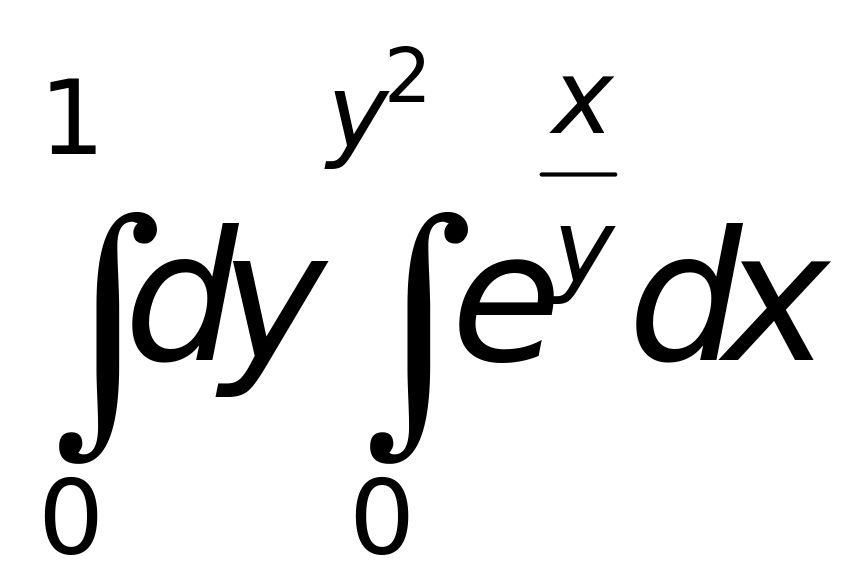в) .