3.2 Структурный анализ рычажного механизма
На рисунке 3.1 изображена схема исследуемого механизма,
где 1 – кривошип; 2 – шатун; 3 – ползун; 0 – стойка.
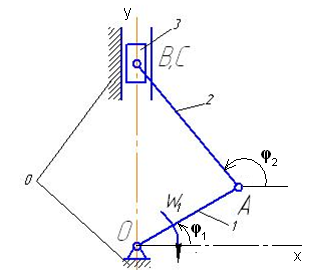
Рисунок 3.1. Схема механизма
Число всех звеньев механизма m = 4.
Число подвижных звеньев механизма n = 3.
Определим класс кинематических пар:
O (0 - 1) - вращательная, одноподвижная, 5 класс;
A (1 - 2) - вращательная, одноподвижная, 5 класс;
B (2 - 3) - вращательная, одноподвижная, 5 класс;
C (3 - 0) – цилиндрическая, одноподвижная, 5 класс.
Число высших пар – р4 = 0.
Число низших пар – р5 = 4.
Так как механизм плоский, то для определения числа степеней свободы механизма используем формулу Чебышева: W = 3·n – 2·p5 – р4
Таким образом, получаем: W = 3·3 – 2·4 – 0= 1.
То, что W = 1 означает, что положение звеньев механизма определяется заданием одной независимой обобщенной координаты входного звена – угла φ1.
Разобьём механизм на группы Ассура и механизм I класса:
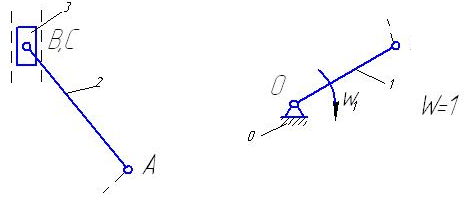
а) б)
Рисунок 3.2. Структурный анализ
На рисунке 3.2.(а) изображена группа Ассура 2 класса, 2 вида, 2 порядка. Механизм на рисунке 3.2.(б) является механизмом 1 класса. Наивысший класс присоединенных групп Ассура – второй, поэтому механизм относится ко второму классу.
Формула строения механизма будет выглядеть следующим образом:
I(0;1)→II(2;3) (3.1)
3.3 Определение размеров звеньев рычажного механизма
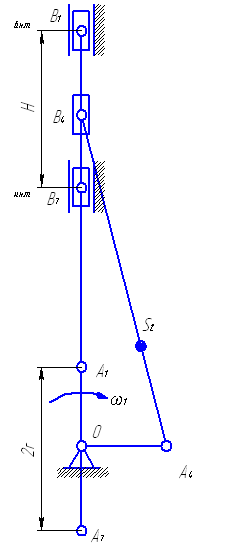
Рисунок 3.3. Расположение механизма в крайних положениях
На рисунке 3.3. изображен механизм в крайних положениях с указанием хода поршня – Н.
Найдем длину кривошипа:
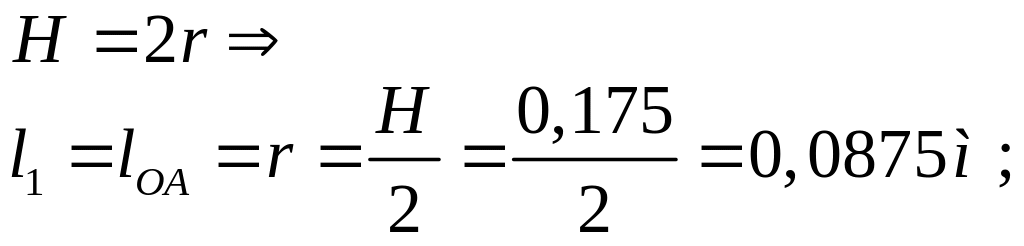
Найдем длину шатуна:
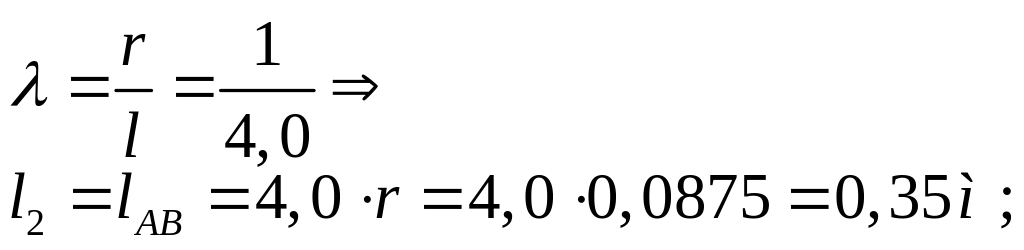
Найдем максимальный угол давления:
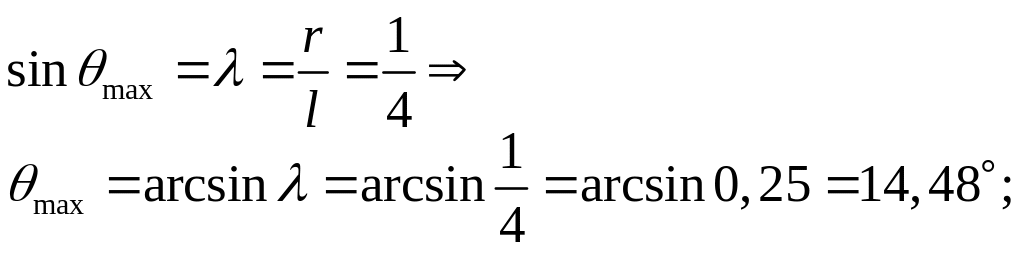
Найдем расстояние
от точки A
до точки S2
(центра масс шатуна 2) из условия:
Определение массы звеньев механизма.
Масса шатуна:
Масса кривошипа:
Масса поршня:
Определим моменты инерции звеньев.
Момент инерции кривошипа:
Момент инерции шатуна:
Определим среднюю угловую скорость кривошипа.
где n1 – частота вращения кривошипа.
где u1H – передаточное отношение планетарной передачи;
nH – частота вращения карданного вала.
В таблице 3.1. сведены основные геометрические характеристики рычажного механизма.
Таблица 3.1. Основные геометрические характеристики рычажного механизма
|
Линейные размеры |
|
Массовые характеристики |
|||||
r, м |
l, м |
|
|
|
|
|
||
188,4 |
0,0875 |
0,35 |
90 |
28 |
3,5 |
1,1 |
0,12 |
0,07 |
3.4 Определение кинематических характеристик рычажного механизма
3.4.1 Графический метод решения
3.4.1.1 Построение плана положений механизма
Рассчитав значения lOA, lAB, lAS2 можно приступить к построению плана положений механизма.
Так как данный механизм имеет вертикальное расположение, то геометрическое место точек всех положений ползуна находится на вертикальной прямой, проходящей через ось вращения кривошипа.
Для построения плана положений механизма необходимо задать масштабный коэффициент, с помощью которого реальные размеры звеньев механизма выражаются в отрезках, изображаемых на чертеже.
Принимаем
Определим значения величин AB и AS2:
На листе формата А1 выбираем точку O и наносим систему координат XOY. Из точки O проводим окружность радиуса OА и разбиваем ее на 12 равных частей. Полученные на окружности точки нумеруем от «1» до «13» (начинаем с верхней, и далее по ходу вращения кривошипа) и соединяем их с центром О. Данные отрезки будут являться положениями кривошипа.
Из точек на окружности проводим отрезки длиной АВ до пересечения их с осью OY и полученные на оси ординат точки нумеруем в соответствии с нумерацией точек на окружности. Данные точки будут являться планом положений ползуна, а отрезки - шатуна.
На плане положений шатуна от точек Ai откладываем отрезки длиной AS2, и полученные точки нумеруем соответственно.
- начальная обобщенная координата,
соответствующая положению механизма
в верхней мертвой точке.