2.5 Геометрический смысл линейных неравенств

Уравнение Ах+Ву+С=0 определяет на плоскости прямую, которая является границей двух полуплоскостей. Координаты любой точки одной полуплоскости удовлетворяют неравенству Ах+Ву+С0, координаты любой точки другой – неравенству Ах+Ву+С0.

Поэтому, чтобы решить, какая именно полуплоскость определяется неравенством Ах+Ву+С0, например, следует подставить координаты конкретной точки в это неравенство. Если получите верное неравенство, то неравенство Ах+Ву+С0 определяет ту полуплоскость, в которой лежит выбранная точка.

Например, решим, какую полуплоскость задает неравенство 2х-3у+60. Построим прямую 2х–3у+6=0 по точкам пересечения ее с осями координат.

Построим полученные точки (-3;0) и (0;2) и прямую.

х -3 0

у 0 2

Рисунок - 29

Координаты точки О(0;0) не удовлетворяют неравенству 2х-3у+60.

Поэтому нужная полуплоскость не содержит точку О. Таким образом, неравенство 2х-3у+60 определяет полуплоскость, лежащую «выше» прямой (заштрихована).

Очевидно, полуплоскость, содержащая начало координат, определяется неравенством 2х-3у+60.

Пример № 6.

Построить множество точек, удовлетворяющих системе неравенств:

1)

Построим две прямые

3х+4у–12=0 и х–4у–4=0

х	4	0		х	4	0
у	0	3		у	0	–1

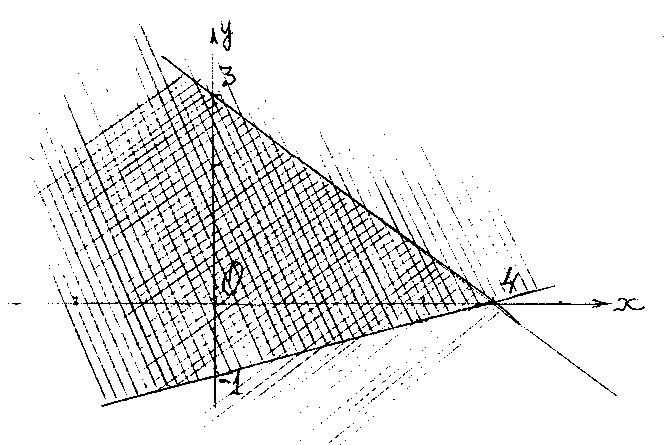
Рисунок - 30

Координаты точки О(0;0) удовлетворяют и неравенству 3х+4у-120 и неравенству х-4у-40. Искомая область – угол, образованный построенными прямыми (двойная штриховка).

2)

Прямая у–4=0 параллельна оси Ох, а неравенство у>4 определяет полуплоскость, лежащую «выше» прямой. Прямая х–у=0 или у=х совпадает с биссектрисой первого и третьего координатных углов. Нужная полуплоскость лежит «ниже» биссектрисы, т. к. у<х.

Искомая область – угол под двойной штриховкой.

Рисунок - 31

3)

2х-3у+6=0 4х-6у-9=0

х	-3	0		х		0
у	0	2		у	0

Искомая область – полоса между двумя параллельными прямыми.

Рисунок – 32

4)

х–у+1=0, х–3у-6+0, х+у+4=0

х	-1	0		х	6	0		х	-4	0
у	0	1		у	0	-2		у	0	-4

Искомая область – треугольник (под тройной штриховкой).

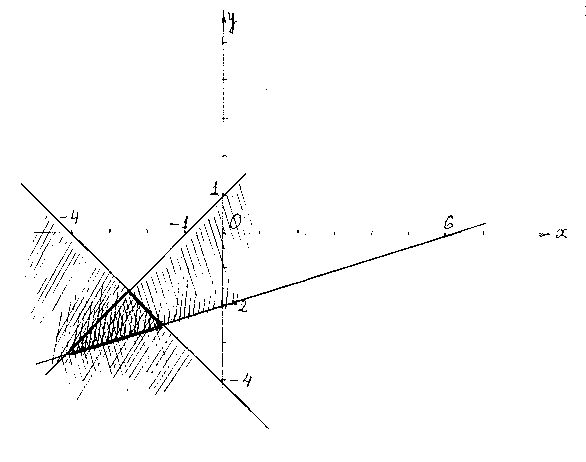
Рисунок - 33

2.6 Уравнение поверхности в пространстве. Плоскость

Введем в пространстве прямоугольную декартову систему координат. Положение любой точки М пространства определяется ее координатами х, у, z.

Поверхность в пространстве рассматривается как множество точек, координаты которых удовлетворяют некоторому уравнению с тремя переменными F(x, y, z)=0. Этому уравнению не могут удовлетворять координаты никакой точки, не лежащей на поверхности. В этом случае уравнение F(x, y, z)=0 называют уравнением поверхности.

Пример № 7

Рассмотрим сферу радиуса R с центром в точке М₀(х₀, у₀, z₀). Так как любая точка М(х, у, z) сферы отстоит от центра на расстояние, равное радиусу сферы, то

или .

Получим уравнение 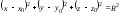, которое и является уравнением сферы.

Простейшей поверхностью является плоскость. Получим уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.

Пусть даны точка М₀(х₀, у₀, z₀) и вектор , перпендикулярный плоскости.

Если точка М(х, у, z) – любая точка плоскости, то вектор лежит в плоскости и должен быть перпендикулярен вектору , т. е. скалярное произведение этих векторов равно нулю:

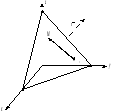
Рисунок - 34

Запишем это условие в координатах.

;

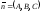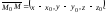
Условие перпендикулярности примет вид: А  (х–х₀) + В  (у–у₀) + С  (z–z₀) = 0

Полученное уравнение и является уравнением плоскости, проходящей через точку М₀(х₀, у₀, z₀) перпендикулярно вектору , который называют нормальным вектором плоскости.

Это уравнение легко привести к виду: А  х + В  у + С  z + D = 0 – общее уравнение плоскости.

Заметим, что уравнение плоскости является уравнением первой степени с тремя переменными. Поэтому плоскость называют поверхностью первого порядка. Ранее полученное уравнение сферы – второй степени относительно х, у, z. Поэтому сфера – поверхность второго порядка.

Рассмотрим уравнения некоторых плоскостей.

Если плоскость проходит через начало координат, то свободный член D в общем уравнении плоскости равен нулю, и уравнение плоскости имеет вид: А  х + В  у + С  z = 0.

Уравнение координатной плоскости Оху можно получить, если в качестве нормального вектора взять вектор , где точка М₁(0,0,1), точка О(0,0,0). Тогда и уравнение координатной плоскости Оху: z=0. Аналогично,

х=0 – уравнение плоскости Оуz,

у=0 – уравнение плоскости Охz.

Рисунок - 35

Очевидно, что уравнения х=a, у=b, z=c определяют три плоскости, параллельные трем координатным плоскостям.

Рисунок - 36

Угол между плоскостями, заданными своими общими уравнениями:

А₁  х + В₁  у + С₁  z + D₁ = 0 и

А₂  х + В₂  у + С₂  z + D = 0

равен углу, образованному нормальными векторам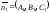и и и вычисляется по формуле

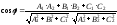. (21)

Условие перпендикулярности двух плоскостей: А₁  А₂ + В₁  В₂ + С₁  С₂ = 0.

Условие параллельности: .

Например, плоскости

2х + 3у – 5z + 7 = 0 и 4х + 6у – 10z – 1 = 0 – параллельны.

Прямую в пространстве можно рассматривать как линию пересечения двух плоскостей А₁  х + В₁  у + С₁  z + D₁ = 0 и А₂  х + В₂  у + С₂  z + D₂ = 0.

Поэтому прямая в пространстве определяется системой двух уравнений первой степени с тремя переменными х, у, z:

общие уравнения прямой.