Тема 2. Аналитическая геометрия

2.1 Декартовы координаты на прямой, на плоскости и в пространстве

Прямую линию с указанным на ней направлением, началом отчета и единицей масштаба назовем числовой осью. Каждому действительному числу Х на числовой оси соответствует единственное число, которое называется координатой данной точки.

Рисунок - 2

Здесь числа х₂х₁0, х₃0.

х₃, х₁, х₂, х - координаты точек Q, F, N, M соответственно. Записывают:

Q (х₃), F (x₁), N(x₂), M (x).

Точки F и N ограничивают отрезок FN. Очевидно, его длина  FN  = х₂- х_1.

Две взаимно перпендикулярные оси на плоскости с общим началом и одинаковой единицей масштаба образуют декартову прямоугольную систему координат на плоскости. Одна из осей - ось абсцисс Ох, другая - ось ординат Оу.

Каждой точке плоскости соответствует единственная пара чисел х, у.

x, у называют координатами точки М и записывают М (х, у).

Рисунок - 3

В пространстве декартова прямоугольная система координат представляет собой совокупность трех взаимно перпендикулярных осей с общим началом и одинаковой единицей масштаба. Это ось абсцисс Ох, ось ординат Оу и ось аппликат Оz. Каждая точка пространства М имеет координаты х, у, z. Записывают: М (х, у, z).

Рисунок - 4

2.2 Вектор. Основные понятия. Действия над векторами

Вектором называется направленный отрезок.

Будем обозначать вектор либо символом , где точки А и В – начало и конец направленного отрезка, либо символом (малая латинская буква с чертой).

Для обозначения длины вектора будем использовать символ модуля:

 – длина вектора ,

 – длина вектора .

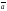Вектор называется нулевым (или нуль-вектором), если начало и конец его совпадают. Нулевой вектор не имеет определенного направления, длина его равна числу 0. Записывают:  = 0.

Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если векторы и коллинеарны, то записывают: .

Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление. Записывают: =.

Понятно, что вектор можно переносить параллельно самому себе в любую точку пространства, т.е. изучаемые в геометрии векторы являются свободными.

Векторы называются компланарными, если они лежат в одной или в параллельных плоскостях.

Рассмотрим векторы, совпадающие с ребрами куба.

Рисунок – 5

Векторы и коллинеарны, но не равны.

Векторы , , 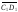, , компланарны, так как лежат в параллельных гранях.

Векторы , , равны: ==.

В квадрате MNKZ векторы , , ,, имеют одинаковые длины, но не равны. Если изменим направление у двух векторов, то можно утверждать, что = и =.

Рассмотрим векторы, совпадающие со сторонами ромба ABCD.

Здесь =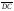, но 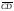, , хотя длины векторов, совпадающих со сторонами ромба, равны:  =  =  = .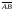

Линейными операциями над векторами называют сложение векторов и умножение вектора на число.

Рисунок - 6

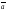Суммой + двух векторов и называется вектор , идущий из начала вектора в конец вектора при условии, что начало вектора совпадает с концом вектора 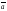. Записывают:

=+.

Рисунок - 7 Рисунок- 8

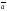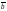Это правило называется "правилом треугольника" (Рисунок -7 ). Для сложения двух векторов можно использовать "правило параллелограмма" (Рисунок -8): если векторы и приложены к общему началу и на них построен параллелограмм, то суммой и этих векторов является вектор, совпадающий с диагональю параллелограмма, идущей из общего начала векторов и .

Сумму трех, четырех и большего числа векторов можно построить по "правилу многоугольника": начало каждого последующего вектора совмещают с концом предыдущего, а суммой всех векторов является вектор, идущий из начала первого вектора в конец последнего. На рисунке 9 построена сумма четырех векторов +++.

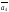Рисунок – 9

Три вектора в пространстве можно складывать по "правилу параллелепипеда": если на трех векторах , ,, как на ребрах, построить параллелепипед, то его диагональ, выходящая из общего начала данных векторов, и будет их суммой (Рисунок 10): =++.

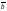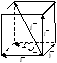
Рисунок - 10

Произведением  вектора на число называется вектор , коллинеарный вектору , имеющий длину, равную , одинаково с вектором направленный в случае 0 и противоположно с ним направленный в случае 0. Записывают: =.

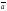Когда =0, для любого вектора произведение  равно нуль-вектору: 0 =.

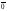Когда =1, 1=.

Когда = 1, (-1)=- - вектор, противоположный вектору .

Итак, при умножении вектора на число получаем вектор, коллинеарный данному. Поэтому, если известно, что =, где - число, имеем два коллинеарных вектора и. Иначе говоря, равенство = является условием коллинеарности векторов и.

Для примера рассмотрим векторы, совпадающие со сторонами треугольника АВС: =, =.

Требуется выразить через векторы и вектор , где О – точка пересечения медиан треугольника.

Известно, что точка О пересечения медиан треугольника делит отрезок медианы в отношении 2:1, считая от вершины. Поэтому =2/3, где точка D – середина стороны СВ.

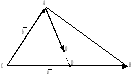
Рисунок - 11

Но вектор =1/2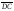=1/2; =-1/2.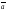

В треугольнике САD вектор =+= -1/2+.

Искомый вектор =-2/3(-1/2+)= 1/3-2/3.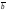

Итак, 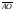=1/3-2/3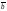. Заметим, что разность векторов и можно рассматривать как сумму вектора и вектора, противоположного вектору :

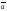–=+(–1) =+(–).

В нашем примере из треугольника САD можно получить вектор =–=1/2–.

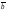Если вектор умножить на число 1/, получим так называемый единичный вектор вектора (или орт вектора ), который обозначается 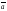₀. Итак, орт вектора или единичный вектор вектора

₀=1/=/; ₀=1.

Принято единичные векторы на координатных осях Ох, Оу, Оz обозначать , , соответственно.

Линейные операции над векторами обладают теми же свойствами, что и линейные операции над матрицами. Укажем некоторые из них:

1) +=+ – перестановочный закон сложения;

2) +(+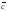)=(+)+ – сочетательный закон сложения;

3) () = () – сочетательный закон умножения на число;

4) (+)=+;

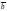5) (+)=+ – распределительные законы.

Рассмотрим координаты вектора, для чего перенесем вектор параллельно самому себе так, чтобы его начало совпало с началом координат. Пусть конец вектора – точка М.

Координатами вектора назовем координаты его конечной точки.

Рисунок - 12

Рисунок – 13

Так как координатами точки на плоскости являются два числа х и у, то на плоскости вектор задается двумя координатами.

Записывают: =(х, у) (Рисунок - 12).

В пространстве вектор задается тремя координатами х, у и z.

Записывают: =(х, у, z) (Рисунок 13).

Нетрудно показать, что при сложении векторов складываются их соответствующие координаты, а при умножении вектора на число все его координаты умножаются на это число.

Если даны координаты векторов и 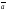=(х₁, у₁, z₁), =(х₂, у₂, z₂) и

=+; =-; =, то координаты векторов , , легко находятся: =(х₁+х₂; у₁+у₂; z₁+z₂),

=(x₁-x₂; y₁–y_2; z₁–z₂),

=(х₁; у₁; z₁).

Видно, что длина вектора равна корню квадратному из суммы квадратов его координат:

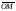==. (10)

В плоском случае достаточно считать третью координату z равной нулю.

Если вектор ограничен двумя точками, координаты которых заданы: т. А (х₁, у₁, z₁), т. В (х₂, у₂, z₂), то легко найти координаты самого вектора .

Рисунок - 14

На рисунке 14 видно, что вектор можно получить как разность векторов и 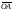, где т. О – начало координат:

=–,

=(х₁, у₁, z₁)_{, =}(х₂, у_2, z₂).

Тогда координаты вектора равны разности соответствующих координат конца и начала вектора: =(х₂–х₁; у₂–у₁; z₂–z₁).

Расстояние между точками А и В вычислим как длину вектора :

АВ==. (11)

Углом между векторами и назовем наименьший угол, на который надо повернуть один вектор до совпадения его с другим.

Рисунок - 15

Записывают ()=.

Покажем угол между вектором и координатной осью Ох, например. Обозначим этот угол через . Пусть =.

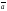Рисунок - 16

Очевидно, что cos==.

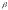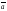Обозначим через , , углы между вектором и координатными осями Ох, Оу, Оz соответственно. Тогда

cos=, cos=, cos=. (12)

Эти формулы определяют направляющие косинусы вектора и полностью задают направление вектора в пространстве. Направляющие косинусы вектора удовлетворяют условию:

cos²+cos²+cos²=1. (13)

Это равенство легко получить, учитывая, что длина вектора

=. (14)

В школьном курсе рассматривается еще одна операция над векторами – скалярное произведение векторов.

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

Обозначают скалярное произведение векторов и символами или (,).

Таким образом, по определению

=cos, (15)

где – угол между векторами и .

Скалярное произведение обладает следующими свойствами:

1. =

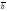
2.

3. (+)=+

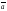
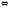
4. Если векторы и взаимно перпендикулярны, то их скалярное произведение равно нулю (и наоборот), т. е. =0.

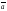
Условие =0 поэтому и называют условием перпендикулярности векторов.

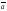
5. =. Отсюда получают правило для вычисления длины вектора: =

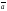
Если известны координаты векторов и , то легко показать, что скалярное произведение равно сумме произведений одноименных координат векторов, т. е. если =(х₁, у₁, z₁) и =(х₂, у₂, z₂), то 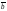=х₁х₂+у₁у₂+z₁z₂

Условие перпендикулярности тогда примет вид: x₁x₂+y₁y₂+z₁z₂=0

Пусть, например, даны векторы = (2, –1, 2), = (1, 0, 4), = (3, 4, –1).

Найдем скалярные произведения

= 2  1 + (–1)  0 + 2  4 = 10,

=2  3 + (–1)  4 + 2  (–1) = 0,

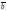
= 1  3 + 0  4 + 4  (–1) = –1.

Мы обнаружили, что векторы и образуют прямой угол.

Используя определение скалярного произведения, можно вычислить угол между векторами по формуле

. (16)