22. Неравенство Чебышева. Сходимость случайных последовательностей.

Для теории вероятности большую роль играют вероятности, которые близки либо к 0, либо к 1. Особую роль при этом играют случайные величины, которые представляют собой сумму большого количества случайных величин.

Последовательность случайных величин ₁, ₂ и т.д. сходится к по вероятности, если для ε>0

Неравенство Чебышева

Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине больше положительного числа , не больше чем, D(x)/ ²_.(дисперсия должна быть ограничена и )

Докажем, это неравенство для непрерывной случайной величины с плотностью вероятности P(X)

Неравенство Чебышева часто используется для противоположного события

23.Теорема Чебышева. Теорема Бернулли.

Теорема Чебышева: Если X₁, X₂,…,X_n – последовательность независимых случайных величин, имеющих конечные дисперсии, ограниченные одним и тем же числом С, то для любого ε >0 выполняется

Доказательство. Введем в рассмотрение случайную величину – среднее арифметическое случайных величин

. Найдем матожидание

И дисперсию

Следовательно – дисперсия конечная. Тогда к применим неравенство Чебышева

Переходя к пределу получим

А так как вероятность не может быть больше 1, то предел равен 1.

Суть закона больших чисел.

Если число случайных величин неограниченно растет, то их среднее арифметическое утрачивает смысл случайной величины и стремится к постоянному числу равному среднему арифметическому их матожиданий.

Следствием теоремы Чебышева является теорема Бернулли.

Пусть - число появления события А в n испытаниях в схеме Бернулли, и p – вероятность появления А в одном испытании. Тогда для любого справедливо -частота появления события.

Пусть , где - число появления события А в i-ом испытании.

Дисперсия любой величины равна произведению pq, так как p+q=1, то p*q не превышает ¼, и следовательно дисперсии всех величин ограничены числом c=1/4

Применим теорему Чебышева: так как матожидание равно вероятности наступления события.

Так как равна относительной частоте появления события А (m/n)(каждая величина _{1, 2}, _n при появлении события в соответствующем испытании равна 1 и поэтому их суму равна m), то окончательно получим , что и т.д.

24. Центральная предельная теорема.

Пусть - последовательность независимых случайных величин и закон распределения не известен.

ЦПТ – называется набор предположений, которые обеспечивают нормальный закон распределения для суммы этих случайных величин

Обозначим через их сумму.

Говорят, что к последовательности применима центральная предельная теорема

Частным случаем ЦПТ является интегральная теорема Муавра-Лапласса.

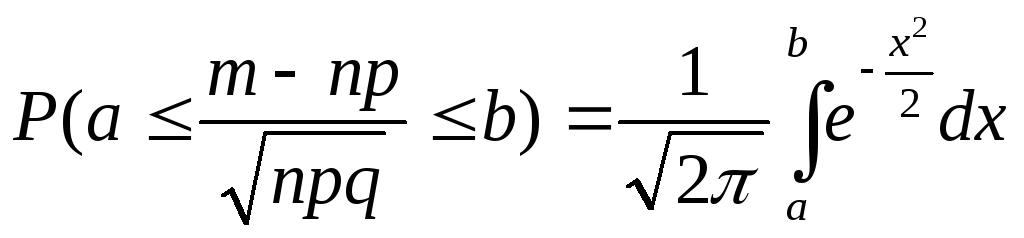
Теорема Муавра-Лапласа утверждает, что если речь не идет о редких событиях, то биноминальное распределение стремится к нормальному.

Сформулируем ЦПТ для одинаково распределенных случайных величин.

Пусть случ величины независимо имеют одинаковые М, D, то к этой последовательности применима ЦПТ.

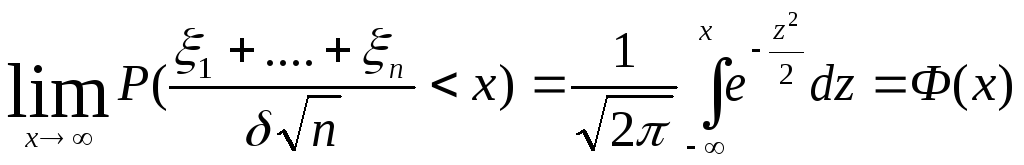
Суть ЦТП

Если число случайных величин неограниченно растет, то закон распределения их сумма стремится к нормальному распределению независимо от того по какому закону распределены слагаемые.