14. Моменты

Начальным моментом порядка k называется матожидание M_k=M

Например первый случайный момент это обычное мо.

Центральным моментом ожидания порядка k называется матожидание в степени k отклонения случайной величины от своего математического ожидания.

Например второй центральный момент это дисперсия.

Любой центральный момент можно выразить через начальный. Например третий центральный момент

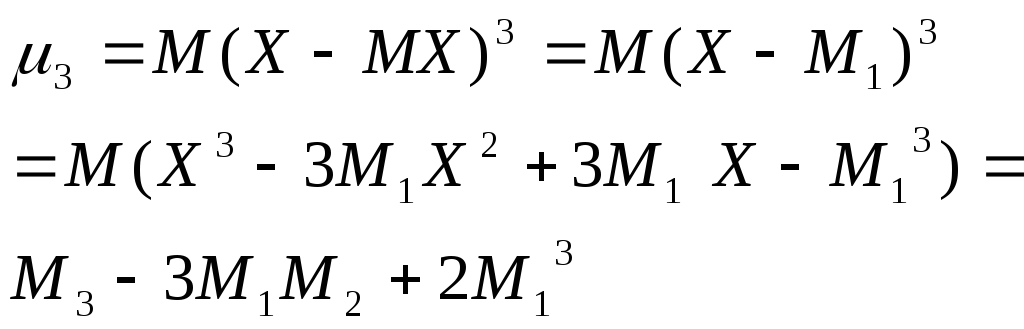
15. Основные дискретные распределения случайных величин.

1. Биноминальное распределение. Рассмотрим схему Бернулли. Производится последовательность n независимых испытаний в каждом из которых возможно только 2 исхода.

P(A)=p P()=q p+q=1

возможное распределение этой величины. Вероятность этих значений вычисляется по формуле Бернулли. .

Найдем МО и DX , где -число появлений события в i-ом (одном) испытании.

Закон распределения

	0	1
P	q	p

МО: M=0*q+1*p=p ; M=np

Чтобы найти дисперсию M₂=0²*q+1²*p=p, D= M_2- (M)²=p-p²=p(1-p)=pq

Так как дисперсии независимы D=npq

2. Распределение Пуассона. Пусть производится n независимых испытаний в каждом из которых вероятность появления события A равна p. Для определения вероятности k пользуется ф. Бернулли. Если вероятность мала, а число испытаний велико то формулой Пуассона.

=0,1,...,m. P_m=

Mξ=∑m*a^m/m!*e^-a =a, Mξ²=∑m² * a^m/m!*e^-a =a+a²

В распределении пуассона МО и Дисперсия равны а

3. Геометрическое распределение. Производится последовательность независимых испытаний в каждом из которых только 2 исхода

P(A)=p P()=q p+q=1

Испытание производится до появления события А. Вероятности этих значений P_m=q^m-1p, P₃=q₂p, ; S = . Если ряд сходится его можно почленно дифференцировать.

D

16. Равномерное и показательное распределение.

Относятся к непрерывным случайным величинам.

1. Равномерное

0, x¢ [a,b]

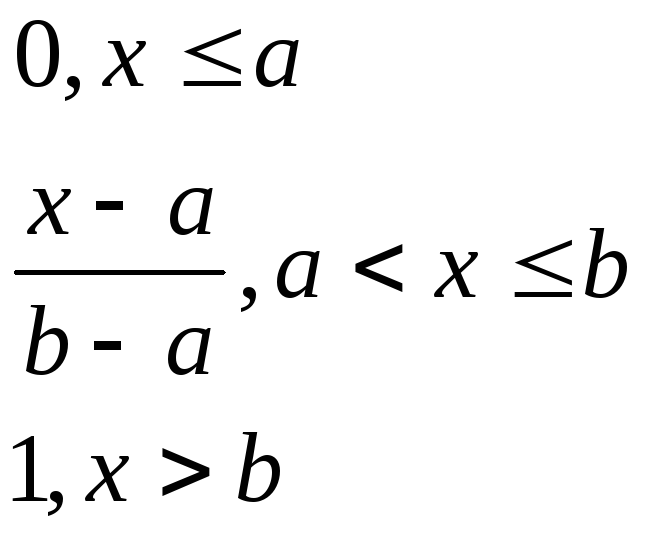M

2. Показательное распределение.

¹

-x

Характерное свойство показательного распределения

17. Нормальное распределение.

Нормальным (распределением Гаусса) называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью.

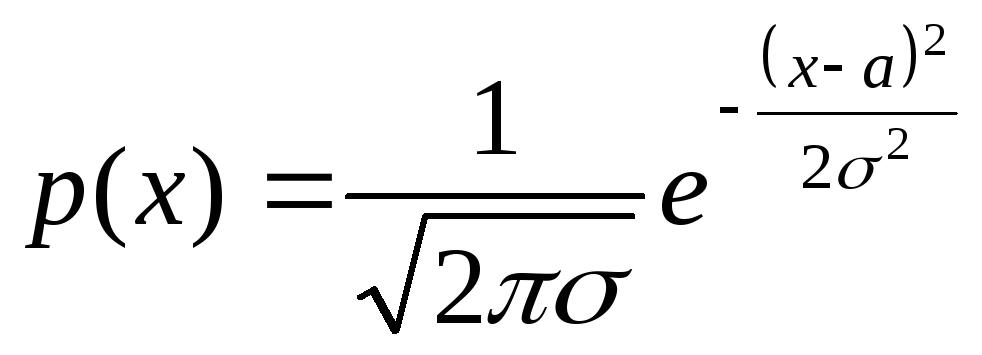
(cигма не под корнем!!)

Нормальное распределение определятся 2 параметрами . а – мат ожидание, - квадратическое отклонение нормального распределения.

Введем новую переменную ,

Тогда

Первое слагаемое – нечетная функция, второе равно a.

M(x)=a Учитывая это

При получим стандартное нормальное распределение.

От произвольного перейти к стандартному можно с помощью преобразования .

Функция стандартного нормального распределения имеет вид.

Часто вместо Ф(x) приводится функция Лапласа (нечетная)

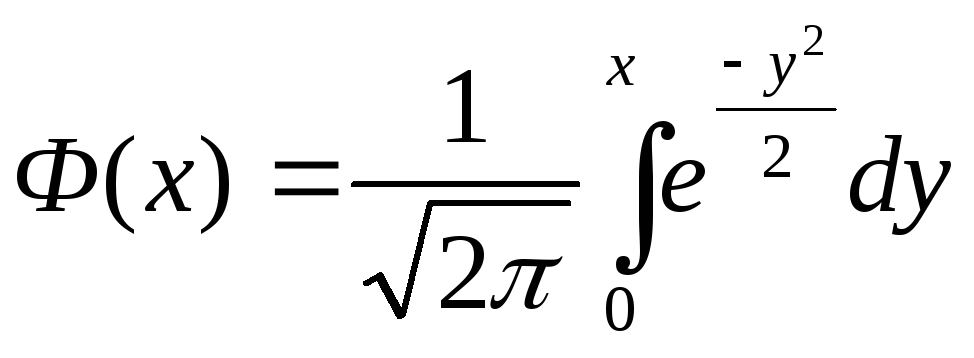F(x)=

Вероятность попадания случайной величины в заданный интервал.

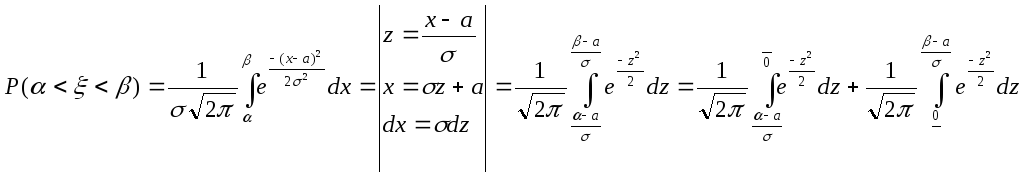
По формуле Лапласа имеем

Вычисление вероятности заданного отклонения от МО для нормальной случайной величины.

Преобразуем данную формулу положив . Получим

Если t=3, то

Т.е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения равна 0.9973. Сущность правила трех сигм: Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического ожидания.