18. Двумерная функция распределения и ее свойства.

Многомерная случайная величина Х=(Х₁, Х₂, ... Х_n) – это совокупность случайных величин Х_i , заданных на одном и том же пространстве элементарных событий

Закон распределения вероятностей многомерной случайной величины Х задается ее функцией распределения

которая является числовой функцией многих переменных и как вероятность принимает значения на отрезке [0,1].

Свойства двумерной функции распределения совпадают с многомерной.

1. 0, так как это вероятность.

2. F(x,y) –неубывающая функция.

3. F(x) непрерывна в каждой точке слева

4.

5.

6. Вероятность того, что случайная точка попадет в замкнутый прямоугольник.

7.

Двумерный дискретный закон распределения изображается в виде таблицы, где в первой строке строчки перечисляются возможные значения случайной величины , в первом столбце возможные значения

Y1	P11	P12		P1n
Y2	P21	P22		P2n
Yn	Pm1	Pm2		Pmn

При этом должно выполняться условие нормировки

Обозначим одномерные законы распределения

	X1		Xn
P	P1		Pn

	y1		yn
P	q1		qn

19. Двумерная плотность вероятности и ее свойства.

Случайный вектор называется непрерывным, если существует такая непрерывная неотрицательная функция p(x,y), что для любых x,yR выполняется соотношение

При этом p(x,y) – двухмерная плотность вероятности.

Свойства.

1. p(x,y)=

2. P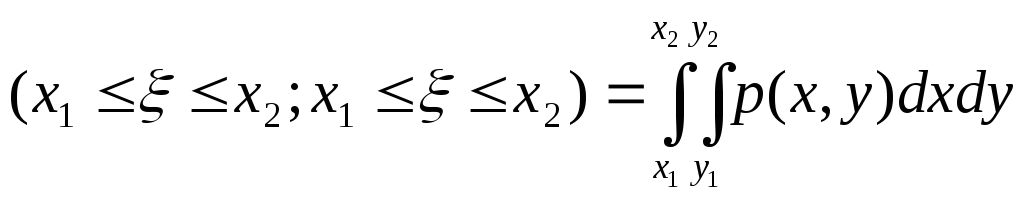

3.

4.

20. Независимость случайных величин

Случайные величины ₁, ₂ называются независимыми, если для любых действительных чисел x₁,…,x_nR случайные события (₁<X₁),…, (_n<X_n) независимы.

Из определения независимых событий вероятность появления должна равняться произведению вероятностей

P(₁<X₁,…, _n<X_n )=P(₁<X₁)…P(_n<X_n)

Случайные события независимы, если многомерная функция распределения равна произведению функций распределения координат.

1. Дискретные случайные величины будут независимы, если . для всех ,

2. Непрерывные случайные величины. Они описываются плотностью вероятности, которая равнв производной n порядка по произв. х_n

p(x,y)= Если случайные величины независимы, то .

21. Условный закон распределения.

Условным законом распределения случайной величины , входящий в систему ( называется ее закон распределения, вычисленный при условии, что принимает значение у.

Пусть ( - непрерывный вектор с плотностью вероятности p(x,y).

Пусть B=(y<<∆y)Тогда условная функция распределения случайной величины при условии, что событие В произошло

Пользуясь формулой умножения имеем

P= 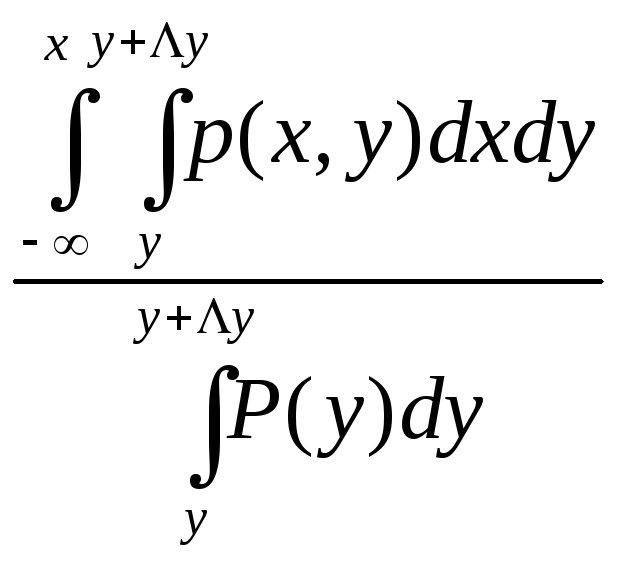(1)

Функция называется условной функцией распределения случайной величины при условии В.

Возьмем производную от (1), устремив при этом ∆y к 0.

(2)

Функция называется условной плотностью вероятности случайной величины при условии, что равен у.

Из (2) следует аналогичная теорема умножения

(3)

Из (3) можем получить непрерывный аналог формулы полной вероятности

Из (2) можно получить условную функцию распределения случайной величины при условии, что равен у.