10. Плотность распределения вероятностей и её свойства.
Плотностью
распределения
вероятностей случайной величины
называется производная
функции распределения:
.
Свойства:
1.
,
,
т. к. это производная неубывающей
функции.
2.
,
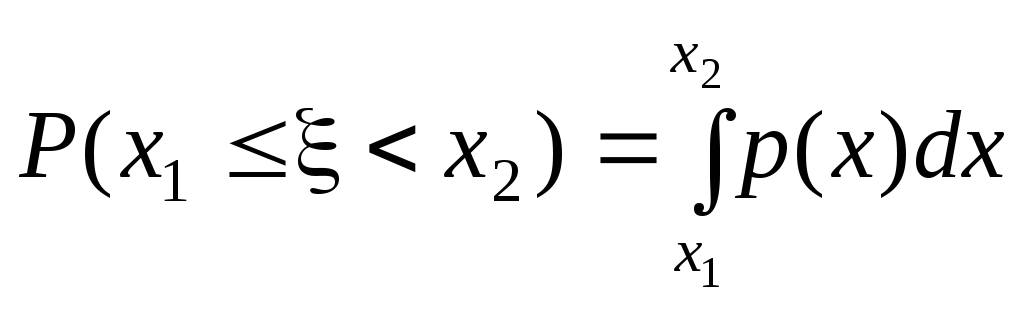т.к.
.
3.
.
Следует из определения и свойства 2.
4.
Свойство
нормировки:
.
В
частности, если все возможные значения
случайной величины заключены в интервале
от a
до b,
то
.
Случайная
величина называется распределенной
по равномерному закону,
если ее плотность вероятности принимает
постоянное значение в пределах заданного
интервала.
11. Математическое ожидание и его свойства.
Для ТВ и ее приложений большую роль играют некоторые неслучайные числа, вычисленные на основании законов распределения случайных величин.
Опр
М
дискретной
СВ
с законом распределения
,
,
называется сумма ряда
,
если этот ряд сходится абсолютно.
характеризует
среднее значение случайной величины,
взвешенное по вероятности.
Опр.
М
непрерывной
СВ
с плотностью вероятности
называется интеграл
=
если он сходится абсолютно., если М=+-беск, то говорят, что м не сущ.
Свойства М
1.
.
2.
М суммы СВ равно сумме их м о-ний:
.
3.
Для независимых
СВ
и
М произведения равно произведению М-ний
=
.
Следовательно,
если а =const.
12. Дисперсия и ее свойства.
Дисперсией
называется
математическое ожидание квадрата
отклонения
(X)
от своего мат. ожидания.
DX=M(X-MX)2=M(X2-2X*MX+(MX)2)=MX2-2(MX)2+(MX)2=MX2-(MX)2, т.е.
DX=MX2-(MX)2
Для дискретной случайной величины с законом распределения xi pi дисперсия равна
D
=
Для равномерного распределения дисперсия зависит от длины отрезка. Чем больше отрезок, тем больше длина дисперсии, ( тем > разбросаны значения вокруг середины отрезка)
Следовательно
дисперсия характеризует рассеяние
возможных значений
вокруг своего математического ожидания.
Средним квадратическим отклонением называется корень квадратный из дисперсии.
Свойства дисперсии
1.DC=0, c=const. Т.к. D(C)=M(C-M(C))2=M(C-C2)=0
2.
Для независимых случайных величин
дисперсия суммы равна сумме дисперсий.
D
(
+η)
= D
+ D
η
3
.
D(
η)=M
2M
η
2-(M
)2(M
η)2
Cледствие:
постоянный множитель выносится за
знак дисперсий с возведением в
квадрат.D(C
)2=C2D(
)
13. Коэффициент корреляции и ковариация.
Коэффициентом корреляции называется
p(
1,
2)=
Свойства
1.
2.
если
1
и
2
независимы, то коэффициент корреляции
равен 0. Обратное не верно. Если p=0,
то говорят, что
1
и
2
некоррелированы.
3.если
1
и
2
связаны линейной функциональной
зависимостью
2=
a+b
1,
то в этом случае [p(
1,
2)]=1
cov
(
1,
2)
=M
[ (
1
-
M
1)(a
+ b
1
–
a
- bM
1)]=bM(
1
-
M
1)2=bD
1
Если
,
то говорят, что
1
и
2
связаны
корреляционной зависимостью, тем более
тесной, чем ближе
к 1.
Коэффициент корреляции служит для количественной характеристики зависимости между случайными величинами.
Если
,
то говорят, что зависимость близка к
линейной.
Ковариацией случайных величин
Cov(
1,
2)=M[(
1-M
1)(
2-M
2)]
Называется произведение отклонений случайных величин от своего МО.
Свойства ковариации
1.
cov(
1,
1)=M(
1-M
1)2=D
1
2. для независимых случайных величин коэффициент ковариации равен 0
cov
(
1,
2)=M
1M
2-M
1M
2=0
Но обратное не верно. Т.е. можно привести пример, когда коэфф. ковариации равен 0, но случайные величины зависимы.
3.
4.
cov
(C
1,
2)=C
cov
(
1,
2)
Ковариация является качественной характеристикой зависимости случайных величин.