
- •1.Случайные события. Действия над событиями.
- •2.Классическое определение вероятности и ее свойства.
- •3.Аксиоматическое определение вероятности.
- •4. Формулы комбинаторики. Гипергеометрическое распределение.
- •5. Условная вероятность. Независимость событий.
- •6. Формула полной вероятности. Формула Байеса.
- •7. Схема независимых испытаний Бернулли.
- •8. Предельные теоремы в схеме Бернулли.
- •9. Функция распределения вероятностей и её свойства.
- •10. Плотность распределения вероятностей и её свойства.
- •11. Математическое ожидание и его свойства.
- •12. Дисперсия и ее свойства.
- •13. Коэффициент корреляции и ковариация.
- •14. Моменты
- •15. Основные дискретные распределения случайных величин.
- •16. Равномерное и показательное распределение.
- •17. Нормальное распределение.
- •18. Двумерная функция распределения и ее свойства.
- •19. Двумерная плотность вероятности и ее свойства.
- •20. Независимость случайных величин
- •21. Условный закон распределения.
- •22. Неравенство Чебышева. Сходимость случайных последовательностей.
- •23.Теорема Чебышева. Теорема Бернулли.
- •24. Центральная предельная теорема.
- •25. Выборочный метод.
- •26. Эмпирическая функция распределения.
- •27. Гистограмма и полигон.
- •28. Числовые характеристики выборки.
- •29. Точечное оценивание.
- •30. Стандартная ошибка точечной оценки
- •32. Распределение , Стьюдента и Фишера.
- •33. Доверительные интервалы для оценки математического ожидания нормального распределения при известном.
- •35 Проверка статистических гипотез.
- •36. Построение критической области.
- •37. Критерий согласия Пирсона.
- •38. Вычисление теоретических частот для нормального распределения.
- •40.Сравнение средних двух нормальных выборок.
- •41. Дисперсионный анализ.
- •42. Парная регрессия.
- •43. Парный коэффициент корреляции, его свойства.
- •44. Проверка гипотез о достоверности коэффициента корреляции.
40.Сравнение средних двух нормальных выборок.
Критерий Стьюдента.
Пусть
имеется 2 выборки с объемами n1
и n2,
распределенные по нормальному закону.
X~N(а1,![]() 1),
Y~N(а2,
1),
Y~N(а2,![]() 2).
2).
Проверим
гипотезу H0
о равенстве матожиданий.H0:a1=a2;
H0:a1![]() a2
a2
Несмещенной
состоятельной оценкой матожидания
является выборочная средняя. H0:![]()
Поэтому H0 можно сформулировать, что средние равны.
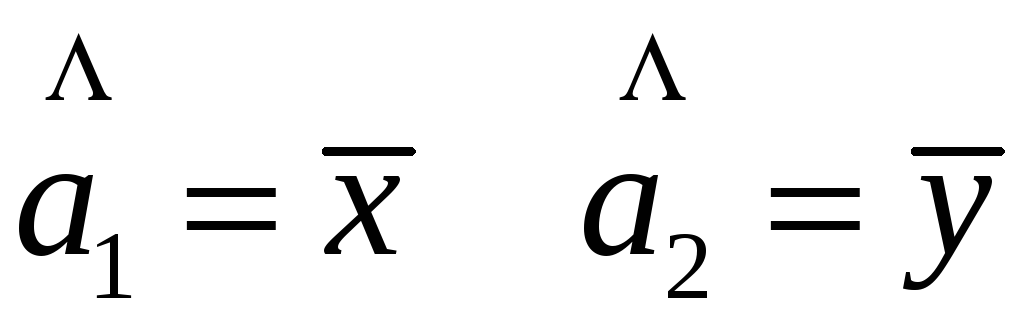
Средние
сравниваются путем вычисления их
разности и построения случайных величин
T=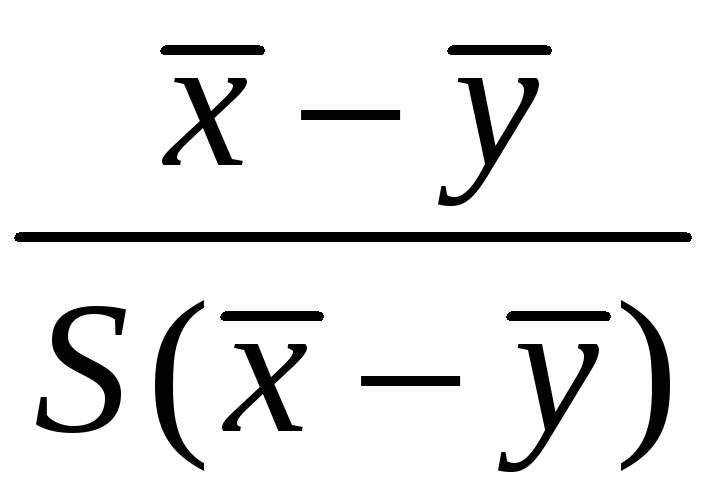 ,
,
![]() )
– ошибка разности средних.
)
– ошибка разности средних.![]()
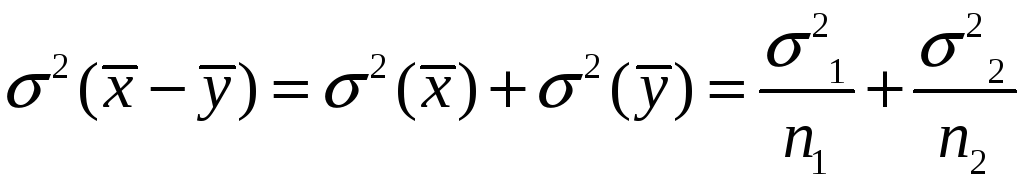
В данной задаче можно представить 4 случая.
1.
![]() и известны.
и известны.
2.
![]() и известны.
и известны.
3.
![]() и неизвестны.
и неизвестны.
4.
![]() и неизвестны.
и неизвестны.
-
T=
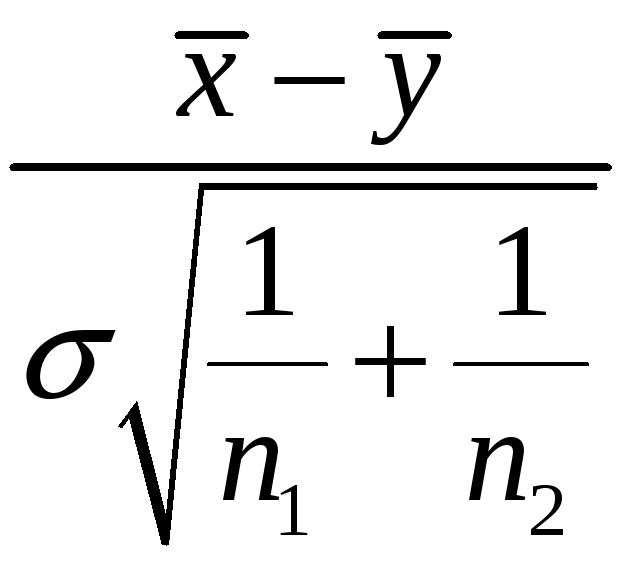 ,
,
В этом случае случайная величина T имеет стандартное нормальное распределение.T~N(0,1)
-
T=
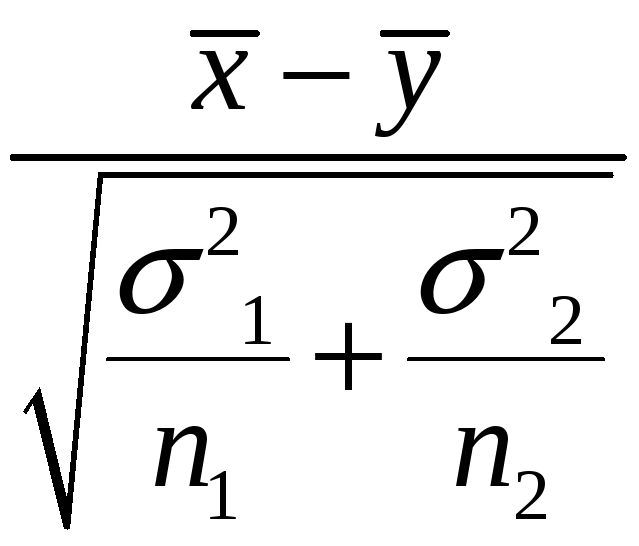 ~N(0,1)
~N(0,1)
Тогда
проверка H0
осуществляется следующим образом:
вычисляются наблюдаемое значение
критерия, по таблице нормального
распределения находят Zкр(![]() ).
Если |Tнабл|>
Zкр(
).
Если |Tнабл|>
Zкр(![]() ),
то H0
отвергаем и принимаем конкуренцию,
следовательно средние значения в
группах различаются равномерно (есть
отклик на воздействие).
),
то H0
отвергаем и принимаем конкуренцию,
следовательно средние значения в
группах различаются равномерно (есть
отклик на воздействие).
-
Если
 неизвестно, то вместо них нужно
подставить оценки
неизвестно, то вместо них нужно
подставить оценки
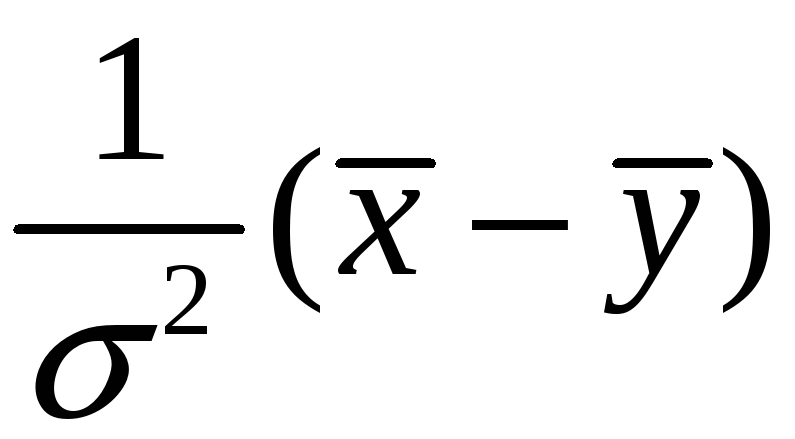 =
=
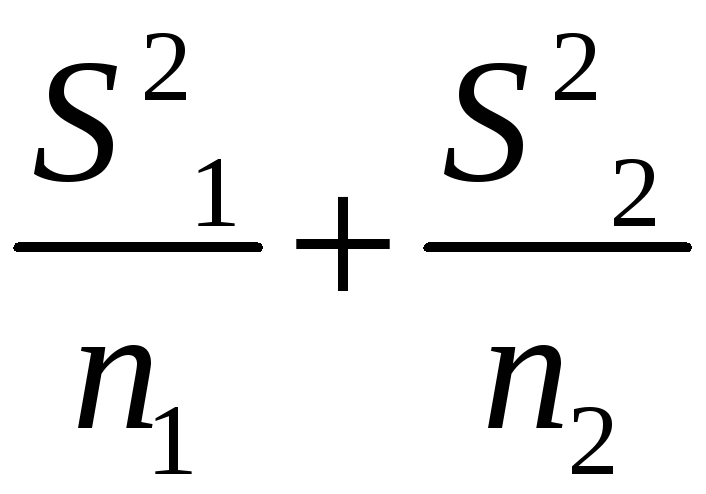
Наблюдаемое
значение критерия T=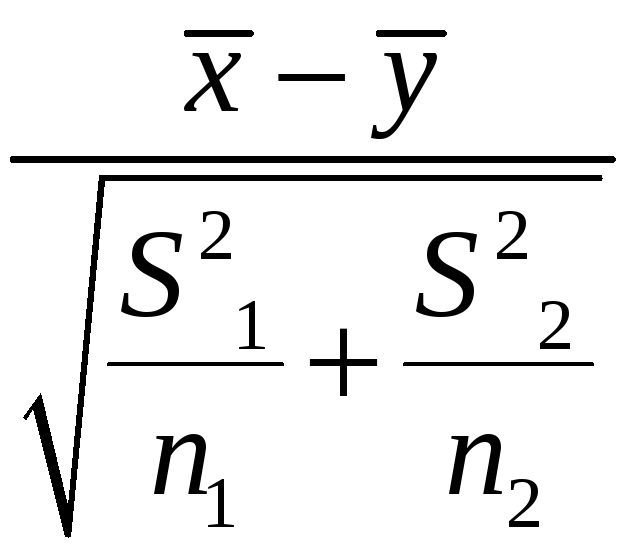 .
.
В
этом случае случайная величина T
имеет распределение Стьюдента с
(n1+n2-2)
числом степеней свободы. Tn~T(n1+n2-2).
Проверка гипотезы осуществляется с
использованием таблиц распределения
Стьюдента по выбранному уровню значимости
![]() и числу степеней свободы (n1+n2-2).
T
кр(
и числу степеней свободы (n1+n2-2).
T
кр(![]() ,
n1+n2-2).
Если |Tн|>|Tкр|,
то H0
отвергаем
и принимает конкурирующую гипотезу,
следовательно средние в группах
различаются достоверно.
,
n1+n2-2).
Если |Tн|>|Tкр|,
то H0
отвергаем
и принимает конкурирующую гипотезу,
следовательно средние в группах
различаются достоверно.
Замечание 1. Критерий Стьюдента применяется, когда n>30.
Замечание 2. Критерий Стьюдента является устойчивым к нарушению нормального распределения изучаемых выборок. В этом случае необходимо только иметь запас уровня значимости.
Если
бы мы могли отвергнуть H0
при
![]() =0.001,
то можно согласиться со следующими
выводами (есть отклик на воздействие).
=0.001,
то можно согласиться со следующими
выводами (есть отклик на воздействие).
-
В этом случае наблюдаемое значение критерия вычисляется по той же формуле, что и в пункте 3, однако точное распределение этой случайной величины указать нельзя. Можно лишь сказать, что при n1, n2
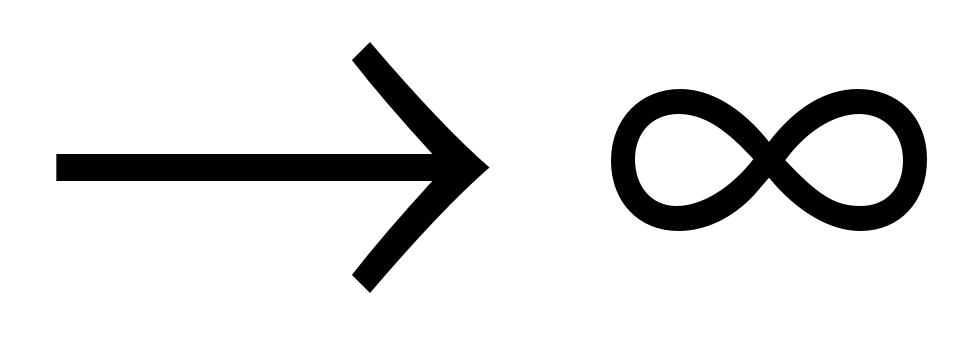 эта
случайная величина будет стремиться
к распределению Стьюдента с числом
степеней свободы
эта
случайная величина будет стремиться
к распределению Стьюдента с числом
степеней свободы
K=
(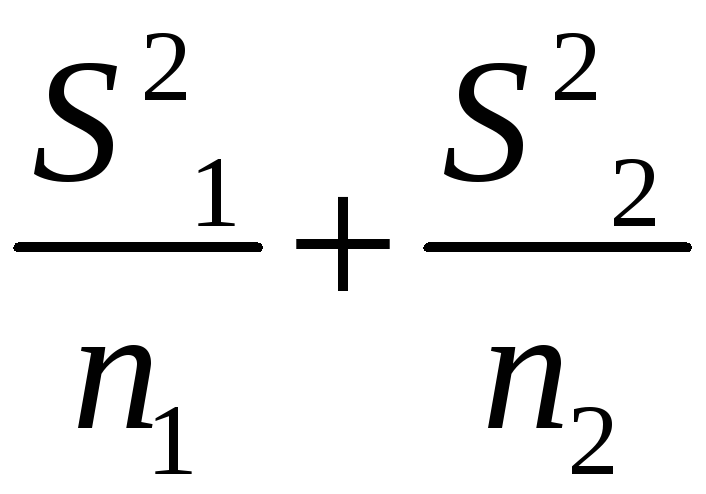 )2/
)2/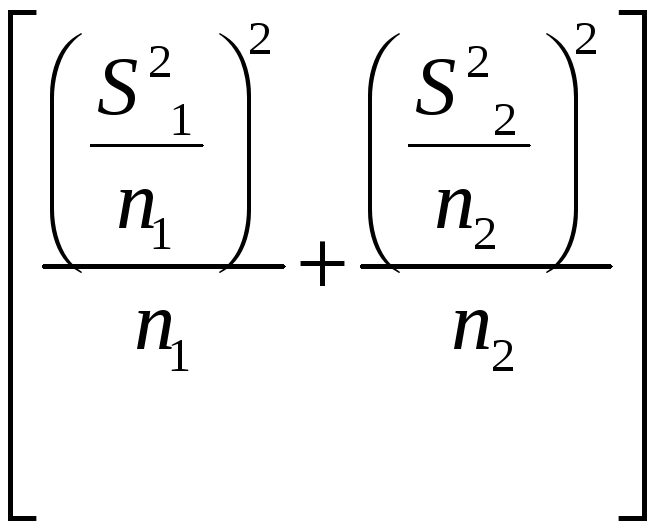 -
-
41. Дисперсионный анализ.
Часто возникает задача в ср-и законов нормального распределения в m группах
H0:F1(x)=…=Fm(x). Например, поступило задание сравнить успеваемость студентов 4 специальностей. Сравнение основывается на вычислении дисперсий. Сравнивают дисперсии, обусловленные влиянием факторов, и дисперсий, обусловленных влиянием случайных величин. Поэтому называется дисперсионный анализ. Если 1 дисперсия достоверно больше 2 дисперсии, то делают вывод о различии функции распределения в группах.
Рассмотрим сначала однофакторный дискретный анализ, т.е. имеется m групп однородных объектов и изучается влияние на них одного фактора. Например, изучаемый признак – успеваемость, а фактор специальность.
Предположим, что каждая группа имеет нормальное распределение
Xi~N(0,1),
i=![]()
Тогда нулевую гипотезу формулируют так H0:a1=…am
Т.к. несмещенной остается ошибкой мат ожидания выборочной средней, то

При конкурирующей гипотезе H1 не все средние равны между собой.
Пусть объемы в группах одинаковы
|
Гр\N |
1 |
2 |
… |
n |
|
|
1 |
X11 |
X12 |
… |
X1n |
|
|
2 |
X21 |
X22 |
… |
X2n |
|
|
… |
… |
… |
… |
… |
… |
|
m |
X31 |
X32 |
… |
X3n |
|
Средние сравнивают между собой. Пусть специальность не влияет на успеваемость.
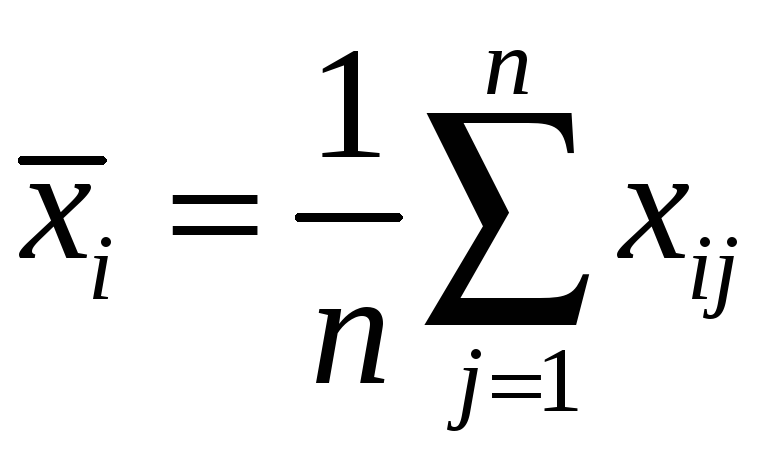 ;
; 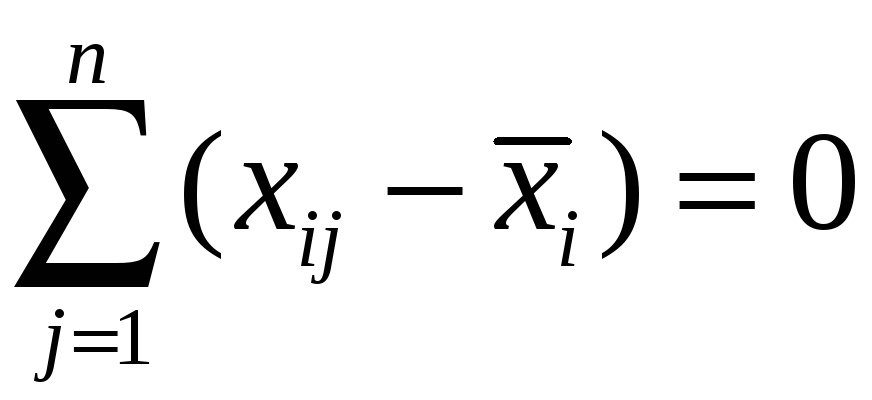 ;
; 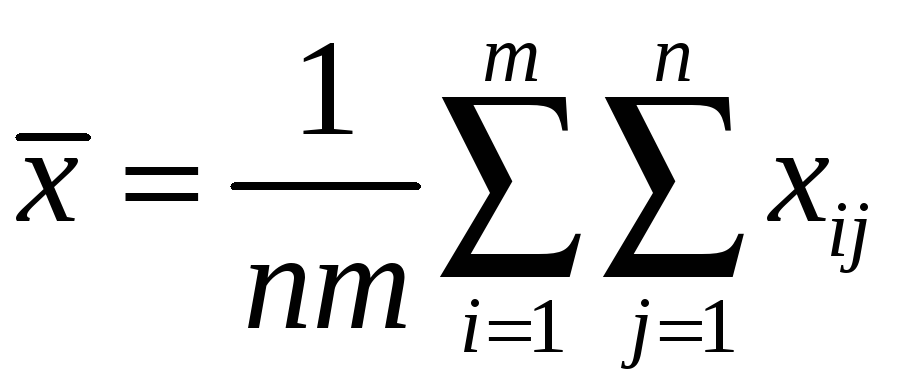 -общая
средняя.
-общая
средняя.
Разложим общую сумму квадратов отклонений на факторную и остаточную
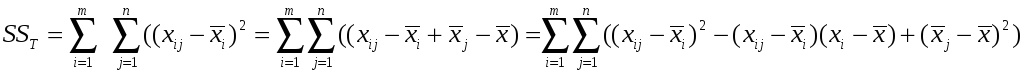
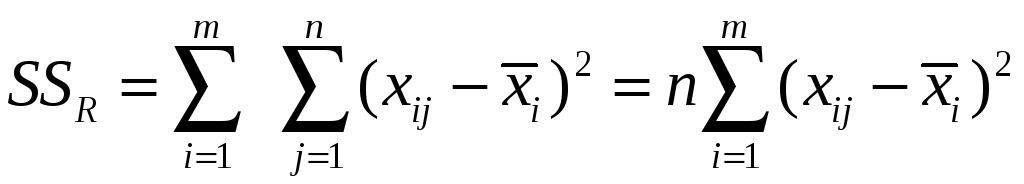 -остаточная
сумма квадратов отклонений, она
обусловлена влиянием случайных величин.
Характеризует рассеяние внутри группы.
-остаточная
сумма квадратов отклонений, она
обусловлена влиянием случайных величин.
Характеризует рассеяние внутри группы.
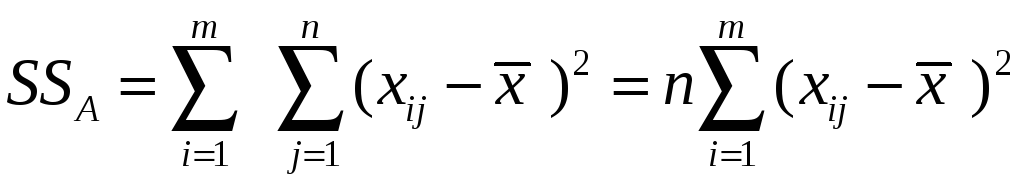 -факторная
сумма квадратов отклонений. Характеризует
рассеяние между группами.
-факторная
сумма квадратов отклонений. Характеризует
рассеяние между группами.
Т.о.
![]() .
Построим
дисперсию по каждой из этих сумм
.
Построим
дисперсию по каждой из этих сумм


Для сравнения факторных и остаточных дисперсий построим их математического ожидания.
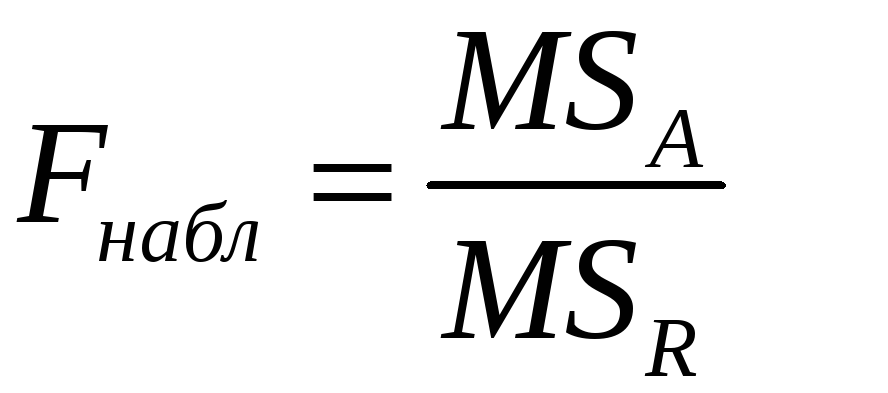
Для справедливости H0 F=0 и чем больше F значение отличное от нуля, тем больше факторная дисперсия. Проверка H0 осуществляется следующим образом:
-
Вычисляем наблюдаемое значение критерия
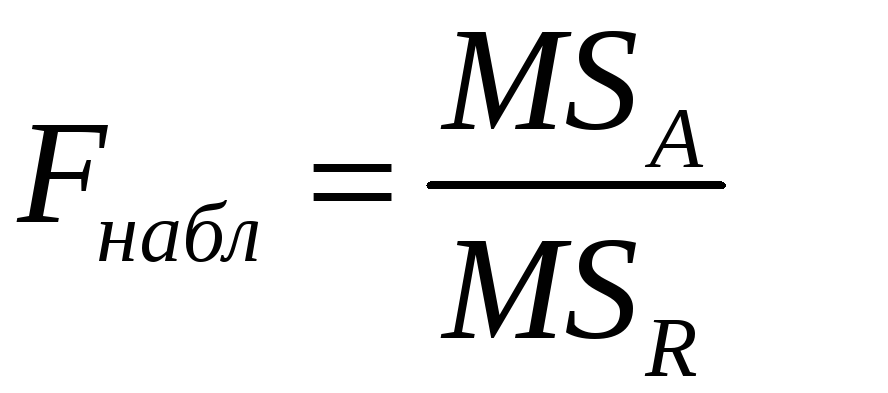
-
По таблице критических точек распределения Фишера по выбранному уровню значимости
 и числу степеней свободы (m-1)
и (mn-m)
находим Fкр.
и числу степеней свободы (m-1)
и (mn-m)
находим Fкр. -
если Fнабл < Fкр., то говорят, что нет основания отвергнуть H0. Следовательно средние в группах различаются недостоверно (случайно). – нет отклика на воздействие. если Fнабл > Fкр., то H0 . отвергается и принимается H1 , следовательно средние в группах различаются достоверно. – есть отклик на воздействие.
Замечание 1. Если Fнабл <1, то сразу H0 принимается.
Замечание 2. Пусть объемы в группах неодинаковы. Значит число степеней свободы остаточной дисперсии N-m.
Замечание
3. Если H0
отвергается, то не все средние в группах
равны между собой. При этом часто
интересует в каких именно группах есть
различия. Если число m
невелико, то это можно установить с
помощью критерия Стьюдента, сделав C![]() попарных сравнений средних. В стандартных
компьютерных программах реализовано
процедура попарного сравнения. Если
выборочные данные Xi
не соответствуют нормальному
распределению, то применение дисперсионного
анализа может привести к ошибочным
выводам. В этом случае необходимо
применить непараметрический дисперсионный
анализ.
попарных сравнений средних. В стандартных
компьютерных программах реализовано
процедура попарного сравнения. Если
выборочные данные Xi
не соответствуют нормальному
распределению, то применение дисперсионного
анализа может привести к ошибочным
выводам. В этом случае необходимо
применить непараметрический дисперсионный
анализ.
