36. Построение критической области.

Рассмотрим построение правосторонней критической области. Пусть вид распределения критерия k для проверки H₀ известен и его плотность P_k(X).

Критическую точку найдем из определения уровня значимости.

; и p_k(x) известны.

Найдем K_кр

;

Рассмотрим построение двусторонней критической области

Раскроем знак модуля и перейдем к правосторонней критической области

;

При компьютерном подходе на основании k наблюдаемого вычисляется минимальное значение уровня значимости при котором H₀ отвергается.

Если P мало(<0.05) то гипотезу отвергают.

37. Критерий согласия Пирсона.

Критерий проверки гипотез о предполагаемом виде распределения называется критерием согласия. Наиболее распространенным из них является критерий согласия Пирсона или критерий .

Пусть вид распределения изучаемого признака Х неизвестен и пусть есть основание предполагать, что он распределен по некоторой функции теоретического распределения. Обозначим

На основании данных выборки построим интервальный вариационный ряд. Для этого найдем:

1. и размах варьирования .

Весь интервал наблюдаемых значений Х разделим на k частичных интервалов одинаковой длины h=R/k k=3,32lgn Левую границу первого интервала возьмем так чтобы хмин попало внутрь интервала z0=xmin- h/2 тогда правая гр последнего интервала может быть zk=xmax +h/2

В результате получим следующий интервал z0<z1<z2<….<zk

2. Подсчитаем число вариант попавших в i-ый интервал

3. Затем для каждого интервала вычислим вероятности попадания случайной величины в построенные интервалы исходя из функции распределения .

4. Теоретические частоты вычислим по формуле .

Критерий Пирсона позволяет ответить на вопрос, значимо ли различаются теоретические и эмпирические частоты. В качестве критерия проверки нулевой гипотезы принимается величина

.

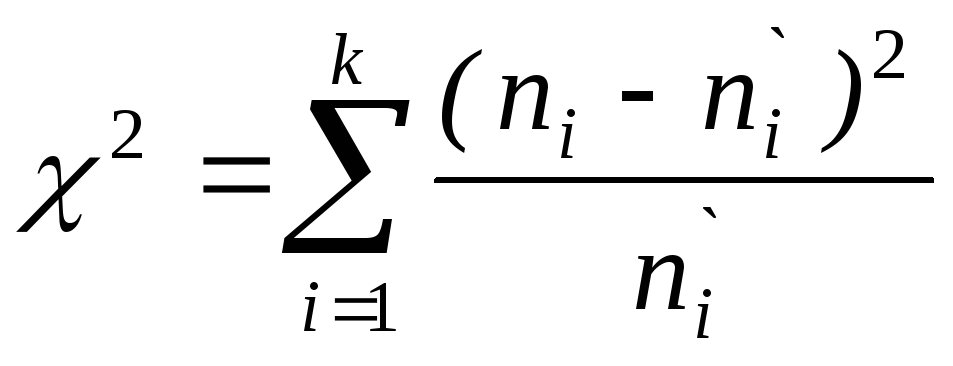Можно доказать, что при закон распределения случайной величины стремится к закону распределения с -степенями свободы =k-l-1, l-число параметров предлогаемого распр. Поэтому случайная величина обозначается через , а сам критерий называют критерием согласия «хи-квадрат».

Правило: Для того чтобы, при заданном уровне значимости проверить гипотезу H₀: генеральная совокупность распределена по закону , надо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия

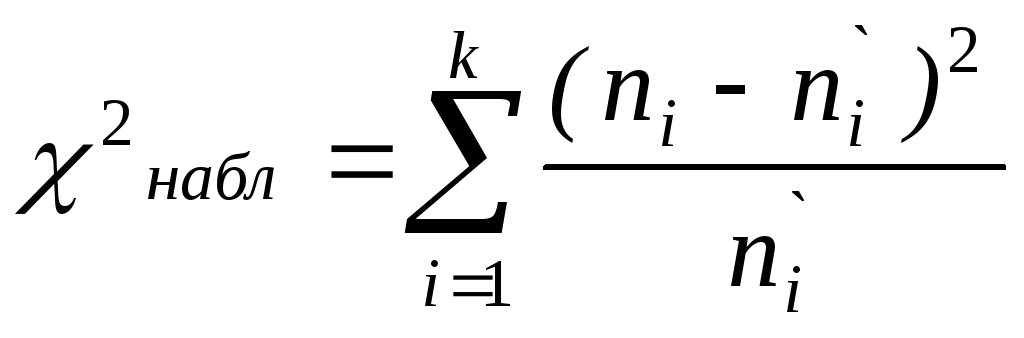и по таблице критических точек распределения , по заданному уровню значимости, и числу степеней свободы , найти критическую точку .

Если , то нет оснований отвергнуть H₀, следовательно, признак Х распределен по закону .

Если , то H₀ отвергаем и принимаем Н₁, следовательно, признак Х распределен по другому законную

Замечание. Для того чтобы эмперич ф-ция распр лучше приближалась к теоретич число интервалов к должно быть большим однако построение критерия хи-квадрат основано на немалых числах ni

Если некоторые частоты малы <5то соседние интервалы объединяються и соответствующие частоты складываются в этом случае число степеней свободы уменьшается на 1