- •1. Электрический заряд. Дискретность заряда. Закон Кулона.
- •2. Напряженность Эл.П. Принцип суперпозиции.
- •3. Работа электростатического поля. Потенциал.
- •4. Связь напряженности с потенциалом Эл.П.
- •60 Применение теоремы Гаусса к расчету электростатических полей
- •70 Статическое поле в веществе. Электрический диполь. Поляризованные заряды. Поляризованность
- •13. Энергия электрических зарядов заряженных проводников и конденсаторов.
- •17. Законы Ома и Джоуля - Ленца в дифференциальной форме
- •18. Правило Киргоффа расчёта разветвлённых электр.Цепей.
- •20. Закон Ома в классической электронной теории
- •21. Сила Ампера. Вектор магнитной индукции
- •22. Закон Био-Савара-Лапласа
- •23. Магнитное поле прямолинейного проводника с током.
- •24. Определение единицы силы тока-Ампера
- •26. Закон полного тока
- •27. Принцип закона полного тока к расчёту магнит поля тороида и длинного соленоида.
- •28. Сила Лоренца
- •29. Эффект Холла. Мгд генератор (магнитогидродинамический)
- •30. Магнитный поток. Теорема Остроградского-Гаусса.
- •31. Контур и виток с током в магнитном поле.
- •32. Явление электромагнитной индукции. Правило Ленца.
- •33. Фарадеевская и Максвеловская трактовка явления электромагнитной индукции
- •34° Самоиндукция. Индуктивность. Коэффициент взаимной индукции.
- •35° Магнитная энергия тока. Плотность магнитной энергии.
- •36. Магнитное поле в веществе. Намагниченность.
- •37. Напряженность магнитного поля.
- •38. Типы магнетиков. Диа- и парамагнетики.
- •39. Феромагнетики. Доменная структура. Техническая кривая намагниченности.
- •40. Ток смещения. С-ма ур-ий электродинамики Максвела в интегр. Форме.
- •41. Уравнения электродинамики Максвелла в дифференциальной форме.
- •42. Скорость распространения электромагнитных возмущений. Волновое уравнение.
- •44. Интерференция света. Когерентность и монохромотичность световых волн. Оптическая длина пути. Время и длина когерентности.
- •45. Расчет интерференциальной картины двух источников
- •46. Интерференция света в тонких пленках
- •47. Дифракция света
- •48. Приближения Френеля. Метод зон Френеля.
- •49. Дифракция Френеля на угол отверстия.
- •51. Дифракционная решётка.
- •52. Принцип голографии.
- •53. Дифракция на пространственной решетке. Формула Вульфа-Брэгга.
- •54. Излучение Вавилова-Черенкова.
- •60. Дисперсия света в области нормальной и аномальной дисперсии.
- •61. Поглащение и рассеивание света
- •55. Поляризация световой волны при отражении. Закон Брюстера.
- •56. Двойное лучепреломление.
- •59° Поляроиды и поляризационные призмы.
- •58. Поляризация света. Закон Малюса .
- •59. Искусственная оптическая анизотропия. Эффект Керра.
- •62. Контактная разность потенциалов. Законы Вольта.
- •63. Термоэлектричество. Эффект Зеебека (1821).
- •64. Эффекты Пельтье и Томсона.
- •65. Пьезоэлектрический и пироэлектрический эффекты.
26. Закон полного тока
Закон
полного тока(теорема о циркуляции
вектора магнитной индукции):циркуляция
вдоль замкнутого контура вектора
магнитной индукции в вакууме равна
произведению магнитной постоянной
0
на
алгебраическую сумму токов
охватываемых
этим контуром:
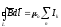 .
Выбор направления обхода контур L
согласовывается с направлением тока
по правилу правого винта. Ток берётся
с «+»если с острия тока I
обход контура совершается против часовой
стрелки иначе «-». Если замкнутый контур
не охватывает проводник с током, то
циркуляция вектора равна В=0. Рассмотрим
доказательство для магнитного поля
бесконечного прямолинейного проводника
с током I
в вакууме. За контур L
возьмем линии индукции В находящихся
на r
от оси проводника с током.
.
Выбор направления обхода контур L
согласовывается с направлением тока
по правилу правого винта. Ток берётся
с «+»если с острия тока I
обход контура совершается против часовой
стрелки иначе «-». Если замкнутый контур
не охватывает проводник с током, то
циркуляция вектора равна В=0. Рассмотрим
доказательство для магнитного поля
бесконечного прямолинейного проводника
с током I
в вакууме. За контур L
возьмем линии индукции В находящихся
на r
от оси проводника с током.
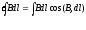 ,
,
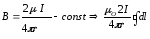




I
r
B
Теорема
о циркуляции вектора магнитной индукции
есть следствие з-на БСЛ, но она допуск
обобщение на поля и люб среды. При таком
обобщении эта теорема – одно из обобщ
электродинамики Максвелла:
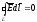 .
Т о цирк в-ра магн инд позвол магн поля
различных конструкций токов.
.
Т о цирк в-ра магн инд позвол магн поля
различных конструкций токов.
27. Принцип закона полного тока к расчёту магнит поля тороида и длинного соленоида.
Применим теорему о циркуляции вектора магнитной индукции. Для вычисления Тороида и длинного соленоида. Тороид – каркас с формой бублика с навитым на него витками проводника по которому течет ток I. Соленоид – цилиндрическая катушка из большого числа намотанного в плотную проводника с током I.
Тороид:
За контур L
возьмем окружность радиуса r
так, что контур внутри тороида. 
Тороид
можно рассмотреть как систему
последовательно соединенных
r
круговых токов одинакового
радиуса и нанизанных на общую
o
R
круговую ось радиуса R.
По
теореме циркуляции имеем
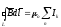
т.к.
контур L
проходит внутри тороида, то он охватывает
ток равный 2πRnI,
где n
– число витков на единицу длины –
плотность витков. Из симметрии вектор
В
в каждой точке напр по касй к L,
тогда
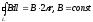 .
Ок-но имеем: В2πr=μ02πRnI
=>
.
Ок-но имеем: В2πr=μ02πRnI
=>
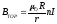 .
Если внутри тороида среда с магнитной
проницаемостью μ, тогда
.
Если внутри тороида среда с магнитной
проницаемостью μ, тогда
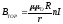 .
.
Соленоид: есть тороид бесконечно большого радиуса, т.е R→∞
N
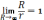
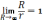
Bсол=μ0μnI
– магнитное
поле соленоида
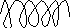
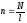 ,
где N
– число витков; l
– длина соленоида
,
где N
– число витков; l
– длина соленоида 
l
28. Сила Лоренца
Сила
Ампера действует на проводник с током,
но токи направленное упорядоченное
движение зарядов. Тогда сила Ампера
должна действовать и на отдельные
движущиеся заряды. Найдем исходя из
силы Ампера выражение для силы действующей
на заряд q
движущейся со скоростью 
 со стороны магнитного поля с индукцией
- сила Лоренца.
со стороны магнитного поля с индукцией
- сила Лоренца. 
B
dl
Рассмотрим проводник длиной
dl
и площадью поперечного сечения S
в 

S
магнитном поле с индукцией. Пусть
ток в проводнике – I.
Заряд q
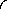



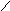

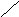

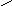
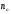 со
скор
со
скор
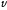 , а
, а
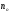 -концентрация
зарядов. На проводник с током
q
действ сила
Ампера:
-концентрация
зарядов. На проводник с током
q
действ сила
Ампера:
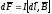 .
Покажем, что эл тока Idl
будет э
I
эквивалентен: qdn
.
Покажем, что эл тока Idl
будет э
I
эквивалентен: qdn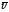 ,
Id
,
Id =qdn
=qdn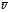 , где q
– заряд; dn
– число зарядов; υ – скорость их движения.
Действительно сила постоянного тока
I=jS,
где S
– площадь поперечного сечения; j
– плотность тока. Умножим на d
, где q
– заряд; dn
– число зарядов; υ – скорость их движения.
Действительно сила постоянного тока
I=jS,
где S
– площадь поперечного сечения; j
– плотность тока. Умножим на d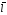 ,
тогда Id
,
тогда Id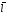 =jSd
=jSd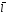 =
=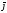 Sdl
=> Id
Sdl
=> Id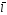 =
=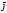 dV,
а
dV,
а
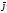 =qn0
=qn0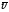 dV,
где n0dV=dn
– число зарядов, тогда Id
dV,
где n0dV=dn
– число зарядов, тогда Id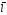 =qdn
=qdn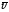 подставим
это выражение в формулу для силы Ампера,
тогда получим
подставим
это выражение в формулу для силы Ампера,
тогда получим
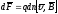 –
сила действующая на рассмотриваемый
проводник в котором число зарядов dn,
тогда сила действующая на один заряд:
–
сила действующая на рассмотриваемый
проводник в котором число зарядов dn,
тогда сила действующая на один заряд:
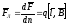 – сила Лоренца, знак q
учитывается. Абсолютны знак силы Лоренца
определяется согласно правилу векторного
произведения: сила Fл
перпендикулярна площади, в
– сила Лоренца, знак q
учитывается. Абсолютны знак силы Лоренца
определяется согласно правилу векторного
произведения: сила Fл
перпендикулярна площади, в
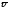
К
которой лежит
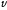 и В. Направление определяется правилом
правого
и В. Направление определяется правилом
правого 

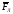
В
и
нта. Если вращать рукоятку правого
винта от первого вектора υ ко
α
второму вектору В на кратчайший
угол α, то поступательное движение

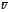
винта
укажет направление силы Лоренца при
положительном заряде:
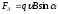 .
Выражение для силы Лоренца зависит от
выбора системы отсчета: если заряд
движется со скоростью
.
Выражение для силы Лоренца зависит от
выбора системы отсчета: если заряд
движется со скоростью 
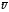 в эл-ском поле с индукцией , то на заряд
будет действовать сила
в эл-ском поле с индукцией , то на заряд
будет действовать сила
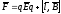 .
Виды траектории зар под действ силы
Лоренца: 1. прямая линия
.
Виды траектории зар под действ силы
Лоренца: 1. прямая линия
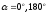 ;
2. окружность
;
2. окружность
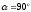 ;
3. цилиндрическая спираль (нарезка винта)
;
3. цилиндрическая спираль (нарезка винта)
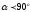 .
.
Магнитное
взаимод проводника с током и действ
магн поля на движ-ся зар предст собой
чисто релитивиский эффект. В сист Гаусса
выраж для силы:
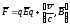 ,
,
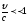 - в сист
Гаусса действ магн поля оч мало (много
меньш эл-ского).
- в сист
Гаусса действ магн поля оч мало (много
меньш эл-ского).