
- •1. Электрический заряд. Дискретность заряда. Закон Кулона.
- •2. Напряженность Эл.П. Принцип суперпозиции.
- •3. Работа электростатического поля. Потенциал.
- •4. Связь напряженности с потенциалом Эл.П.
- •60 Применение теоремы Гаусса к расчету электростатических полей
- •70 Статическое поле в веществе. Электрический диполь. Поляризованные заряды. Поляризованность
- •13. Энергия электрических зарядов заряженных проводников и конденсаторов.
- •17. Законы Ома и Джоуля - Ленца в дифференциальной форме
- •18. Правило Киргоффа расчёта разветвлённых электр.Цепей.
- •20. Закон Ома в классической электронной теории
- •21. Сила Ампера. Вектор магнитной индукции
- •22. Закон Био-Савара-Лапласа
- •23. Магнитное поле прямолинейного проводника с током.
- •24. Определение единицы силы тока-Ампера
- •26. Закон полного тока
- •27. Принцип закона полного тока к расчёту магнит поля тороида и длинного соленоида.
- •28. Сила Лоренца
- •29. Эффект Холла. Мгд генератор (магнитогидродинамический)
- •30. Магнитный поток. Теорема Остроградского-Гаусса.
- •31. Контур и виток с током в магнитном поле.
- •32. Явление электромагнитной индукции. Правило Ленца.
- •33. Фарадеевская и Максвеловская трактовка явления электромагнитной индукции
- •34° Самоиндукция. Индуктивность. Коэффициент взаимной индукции.
- •35° Магнитная энергия тока. Плотность магнитной энергии.
- •36. Магнитное поле в веществе. Намагниченность.
- •37. Напряженность магнитного поля.
- •38. Типы магнетиков. Диа- и парамагнетики.
- •39. Феромагнетики. Доменная структура. Техническая кривая намагниченности.
- •40. Ток смещения. С-ма ур-ий электродинамики Максвела в интегр. Форме.
- •41. Уравнения электродинамики Максвелла в дифференциальной форме.
- •42. Скорость распространения электромагнитных возмущений. Волновое уравнение.
- •44. Интерференция света. Когерентность и монохромотичность световых волн. Оптическая длина пути. Время и длина когерентности.
- •45. Расчет интерференциальной картины двух источников
- •46. Интерференция света в тонких пленках
- •47. Дифракция света
- •48. Приближения Френеля. Метод зон Френеля.
- •49. Дифракция Френеля на угол отверстия.
- •51. Дифракционная решётка.
- •52. Принцип голографии.
- •53. Дифракция на пространственной решетке. Формула Вульфа-Брэгга.
- •54. Излучение Вавилова-Черенкова.
- •60. Дисперсия света в области нормальной и аномальной дисперсии.
- •61. Поглащение и рассеивание света
- •55. Поляризация световой волны при отражении. Закон Брюстера.
- •56. Двойное лучепреломление.
- •59° Поляроиды и поляризационные призмы.
- •58. Поляризация света. Закон Малюса .
- •59. Искусственная оптическая анизотропия. Эффект Керра.
- •62. Контактная разность потенциалов. Законы Вольта.
- •63. Термоэлектричество. Эффект Зеебека (1821).
- •64. Эффекты Пельтье и Томсона.
- •65. Пьезоэлектрический и пироэлектрический эффекты.
41. Уравнения электродинамики Максвелла в дифференциальной форме.
Здесь
установлена локальна связь (в точке)
величин, описывая электронные поля.
Применим теорему Стокса к левым частям
уравнений (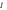
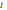 )
и (
)
и (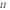
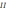 ):
«циркуляция в-ра
):
«циркуляция в-ра
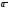 вдоль замкнутого контура L
= потоку в-ра
вдоль замкнутого контура L
= потоку в-ра
 через
пов-ть S
огранич этим контуром»:
через
пов-ть S
огранич этим контуром»:
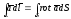 .
.
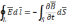
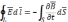 (
(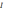
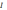 )
)
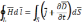
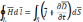 (
(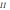
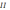 )
)
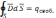
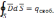 (
(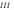
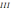 )
)
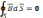
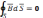 (
(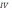
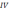 )
)
Пусть:
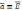 ,
,
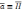 .
Тогда:
.
Тогда:
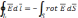 ,
,
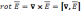
Уравнение
(I)
примет вид:
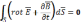 .
S-любая
поверхность, подынтегральное выражение
=0, т.е
.
S-любая
поверхность, подынтегральное выражение
=0, т.е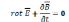
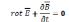 .
.
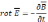
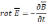
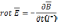
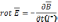 .
.
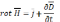
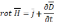

 Ур-я III
и IV
зап в диф форме по т. Остр-Г: «поток в-ра
Ур-я III
и IV
зап в диф форме по т. Остр-Г: «поток в-ра
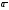 через замкн пов-ть S
= интегр от дивергенции
через замкн пов-ть S
= интегр от дивергенции
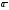 по всему объёму V
огран этой пов-тью»:
по всему объёму V
огран этой пов-тью»:
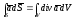
Пусть:
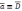 ,
,
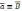 .
Левая
часть уравнения III
примет вид:
.
Левая
часть уравнения III
примет вид:
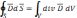
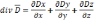 ,
,
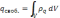 С
учетом сказанного, уравнение III
в дифференциальной форме:
С
учетом сказанного, уравнение III
в дифференциальной форме:
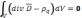

 -произвольный,
то
-произвольный,
то 
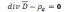
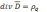
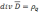
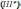
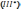 .
.
 Аналогично
уравнение IV:
Аналогично
уравнение IV:


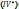
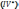
42. Скорость распространения электромагнитных возмущений. Волновое уравнение.
Из
уравнения электродинамики вытекает
существование электромагнитных волн.
Это существование обуславливается
наличием тока смещения 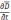
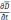 .
Получим волновое уравнение для
распростанения электромагнитных
колебаний в однородной изотропной среде
(
.
Получим волновое уравнение для
распростанения электромагнитных
колебаний в однородной изотропной среде
(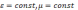
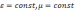 ),
нейтральной среде
),
нейтральной среде 
 ,
непроводящей (
,
непроводящей (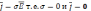
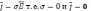 ).
).
Тогда с учетом связи
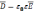
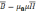
Уравнения
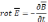
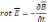
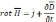
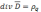

примут вид:

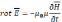 (1)
(1)
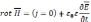
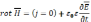 (2)
(2)
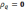

 (3)
(3)
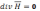
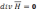 (4)
(4)
Возьмем частную производную от уравнения от уравнения (2)
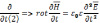
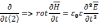 (5)
(5)
Из уравнения (1) имеем
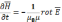
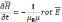 (6)
(6)
подставаим
из (6) 
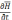 в уравнение (5)
в уравнение (5)
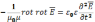
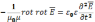 (7)
(7)

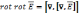


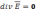
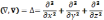
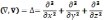 (8)
(8)
Уравнение (7) с учетом (8) имеет вид:
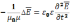
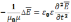 (9)
(9)

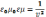
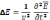
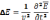

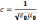
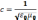


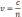
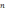
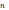 -покеазывает
во сколько раз скорость света больше
чем скорость в среде
-покеазывает
во сколько раз скорость света больше
чем скорость в среде
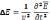
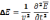 (10)- волновое уравнение
(10)- волновое уравнение
Скорость электромагнитных волн совпадает со скоростью света, данный факт привел Максвелла к выводу, что свет - Электромагнитная волна.
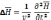
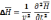 (11)
(11)
Решениями (10) и (11) является уравнение в однородном случае:
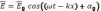
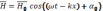


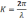
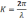 -волновое
число
-волновое
число 
 -смещение
от источника
-смещение
от источника
44. Интерференция света. Когерентность и монохромотичность световых волн. Оптическая длина пути. Время и длина когерентности.
Оптика
– учение о свете и его взаимод с в-вом.
Свет им двойств природу: волновую,
корпускулярную. Волновая оптира рассм
свет как эл-магн волну с
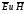 :
1.
:
1.
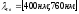 фиол-кр,
фиол-кр,
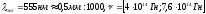 кр-фиол,
кр-фиол,
 кр-фиол; 2. свет – поток фатонов, с=3*108м/с.
кр-фиол; 2. свет – поток фатонов, с=3*108м/с.
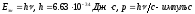 .
На глаз чел и приборы основное возд оказ
в-р
.
На глаз чел и приборы основное возд оказ
в-р
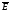 ,
,
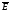 -наз световым в-ром. В-р
-наз световым в-ром. В-р
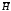 - значит меньш возд. Интерференция света
– явл усиления и ослабления свет колеб
при налож когер волн. Две волны наз когер
если они им постоян во врем разность
фаз:
- значит меньш возд. Интерференция света
– явл усиления и ослабления свет колеб
при налож когер волн. Две волны наз когер
если они им постоян во врем разность
фаз:
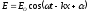 ,
когер могут быть лишь волны с один
частотой
,
когер могут быть лишь волны с один
частотой
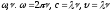 .
Монохроматические в-ны – в-ны с одинак
частотой. Интерференция наблюд лишь
для волн у кот колеб в-ра
.
Монохроматические в-ны – в-ны с одинак
частотой. Интерференция наблюд лишь
для волн у кот колеб в-ра
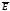 наблюд
в одной пл-ти. Рассм налож 2-ух волн:
наблюд
в одной пл-ти. Рассм налож 2-ух волн:
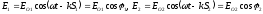 .
Из теории колеб известно, что рез колеб
будет гармонич с такой же частотой и
амплитудой =:
.
Из теории колеб известно, что рез колеб
будет гармонич с такой же частотой и
амплитудой =:
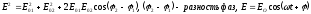 .
1).
.
1).
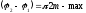
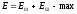 ;
2)
;
2)
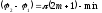
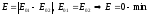 .
.
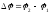 - склад (накл) волн. Получим усл мах и мин
на языке разнасти хода свет волн. Тогда
ур волн:
- склад (накл) волн. Получим усл мах и мин
на языке разнасти хода свет волн. Тогда
ур волн:
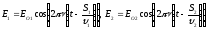 ,
,
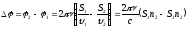 ,
,
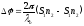 .
Оптической длиной l,
геометрического пути S,
наз в-на: l=Sn,
т.е. произв геом пути на покозатель
преломления среды. Оптич разность хода
.
Оптической длиной l,
геометрического пути S,
наз в-на: l=Sn,
т.е. произв геом пути на покозатель
преломления среды. Оптич разность хода
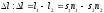 .
Разность фаз:
.
Разность фаз:
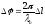 .
1)
.
1)
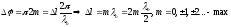 .
Им
интерференционный мах, если оптич разн
хода = чётному числу длин полуволн в
вакууме, или целому числу длин волн. 2)
.
Им
интерференционный мах, если оптич разн
хода = чётному числу длин полуволн в
вакууме, или целому числу длин волн. 2)
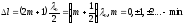 .
Им интерф мин, если оптич разн хода 2-ух
когер волн = нечётному числу длин полуволн
в вакууме или = нецелому числу длин волн.
Если разность фаз меняется случайно во
времени, то волны не когерентны.
.
Им интерф мин, если оптич разн хода 2-ух
когер волн = нечётному числу длин полуволн
в вакууме или = нецелому числу длин волн.
Если разность фаз меняется случайно во
времени, то волны не когерентны.
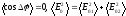 -
перераспред интенсивности света в
простр не происх. Естествен источн света
(не лазер) излуч не когер волны, т.к.
каждый атом в-ва излуч независимо. Различ
временную и простр когер. Кажд атом
излуч послед или цуг волн
-
перераспред интенсивности света в
простр не происх. Естествен источн света
(не лазер) излуч не когер волны, т.к.
каждый атом в-ва излуч независимо. Различ
временную и простр когер. Кажд атом
излуч послед или цуг волн
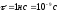 ,
волны 1 цуга когерентны
,
волны 1 цуга когерентны
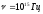 ,
кажд цуг излуч 106
волн (когер), т.к. распр со скор 3*108м/с,
то длина цуга Lког=0,3м.
для лазара: Lког=1000м.
Простр когер - когер-ть лучей исходящих
из протяжённого источника при этом
область отчётл интерфер картины им
опред разм.
,
кажд цуг излуч 106
волн (когер), т.к. распр со скор 3*108м/с,
то длина цуга Lког=0,3м.
для лазара: Lког=1000м.
Простр когер - когер-ть лучей исходящих
из протяжённого источника при этом
область отчётл интерфер картины им
опред разм.
