1. Электрический заряд. Дискретность заряда. Закон Кулона.

Из опытов следует, что тела, например при трении, способны наэлектризовываться, т.е. приобретать Эл/з. наэл тела взаим между сабой. Сущ. два вида Эл/з, условно называемые «+» и «-». Из опытов следует, что Эл/з дискретен, т.е. Эл/з q тела: q =Nе, N=0,1,2,3… е- элементарный зар. е=1,6*10ˉ¹⁹Кл. Носителем «-» Элем/з явл. электрон , «+» зар. ядро атома водорода, протон или позитрон. 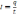Единицей измерения Эл/з в СИ Кулон (Кл), он определяется из силы тока 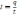⇒ q=It 1Кл=1А*1с. Кулон –зар. проходящий через поперечное сечение проводника за 1с при силе тока в проводнике 1А. Для Э/з споведл з-н сохр: «суммарный заряд электрич изолир сист сохран во врем». 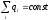. Система электрически изолированная, если через ее границу не проходят зар. тела. Электростатика изучает з-ны взаимодействия неподвижных зар. Основной З. электростатики – З.Кулона (1785): «сила взаимод 2-ух точечных неподвижных Э/л зар в вакууме прямопропорц произвед модулей этих зарядов и обратно пропорц квадр раст между зар». 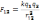. Сила направленная по прямой, соединяющих зар. так, что одноименные зар. отталкиваются, а разноименные притягиваются. Зар. точечный, если размеры зар. тел малы по сравнению с расстоянием между ними. к - к-т пропорциональности 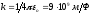, - электрическая постоянная, =8,85*10^-12Ф/м.

Диэлектрическая проницаемость показывает во сколько раз сила взаимодействия задов в среде меньше, чем в вакууме. 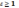. ε_вак=1, ε_стекла=4/3, ε_воды=81. З.Кулона в векторном виде:

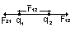
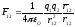
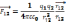
2. Напряженность Эл.П. Принцип суперпозиции.

Взаимодействие между покоящимися зар. осуществляется посредством Эл.п. (электро-статического поля) . понятие Эл.п. ввел Фарадей. Неподвижный Эл.зар. изменяет свойство пространства и создает Эл.п. Оно проявляется по действию на пробный зар. Отношение силы действующей со стороны поля на пробный зар. не зависит от величины этого зар. и может хар-ть само Эл.п. , тогда приходим к характеристике поля – напряженности :

Эл.п. эсть векторная силовая характеристика поля = отношению силы, действующей на зар. со стороны поля,к зар. , т.е.: 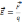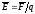, q≷0, Напряженность поля численно = силе, действующей на единичный «+» зар. 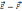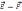, когда q=+1. Единицы измерения напряжения 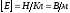, 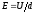. Найдем напряжение поля точечного зар. q , находящейся в точке. Хар. вектором в среде, по З.Кулона можем записать

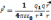
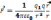
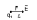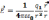
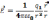, - созд. точечный зар.

Если известна Е , то сила со стороны поля действующая на зар. q =:

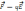
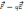
Сила F, действующая на пробный зар. q в данной точке поля, = векторной сумме сил каждого зар. в отдельности, т.е.: 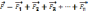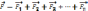, помножим на

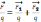
… т.е. 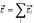- принцип суперпозиции .

Напряженность Эл.п. системы зар. = векторной сумме напряженностей полей, создаваемых каждым зар. в отдельности.

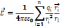
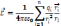
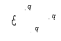
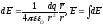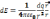
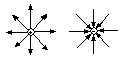
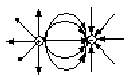
Если непрерывно распределенный зар. т.е. : . 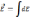Эл.п. графически изображается с помощью линий напряженности Е, силовых линий, линий Е, метод предложил Фарадей. Линии напряженности это кривые, касательный к которым в каждой точке совпадают с направлением вектора напряженности в данной точке. Линии напряженности начинаются на «+» зар. и заканчиваются на «-» или уходят в . Густота силовых линий ,т.е. число линий на ед. площади поверхности перпендикулярной к линиям. Она выбирается так, что количество линий пронизывающих ед. площади поверхности равно или пропорционально . 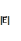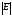По силовым линиям можно судить о величине и направлении вектора в разных точках пространства. Рассмотрим примеры силовых линий: