3. Формулы полной вероятности и формула Байеса

Если об обстановке опыта можно сделать n исключающих друг друга предположений (гипотез)  

Н₁, Н₂, ..., Н_n

и если событие А может появиться только при одной из этих гипотез, то вероятность события А вычисляется по формуле полной вероятности:

Р(А) = Р(Н₁) Р(А/Н₁) + Р(Н₂) Р(А/Н₂) +...+  Р(Н_n) Р(А/Н_n)

или   

где Р(Н_i) - вероятность гипотезы Н_i; Р(А/Н_i) - условная вероятность события а при этой гипотезе.

Если до опыта вероятности гипотез были Р(Н_i), P(H_i),...,P(H_n), а в результате опыта появилось А, то с учетом этого события "новые", т.е. условные вероятности гипотез вычисляются по формуле Байеса:

     (i = 1, 2, ..., n)

Формула Байеса дает возможность "пересмотреть" вероятности гипотез с учетом наблюдательного результата опыта.

Если после опыта, закончившегося появлением события А, производится еще один опыт, в котором может появится или не появиться событие В, то вероятность (условная) этого последнего события вычисляется по формуле полной вероятности, в которую подставлены не прежние вероятности гипотез Р(Н_i), а новые Р(Н_i/А):

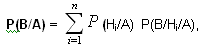
4. Формула Бернулли — формула в теории вероятности, позволяющая находить вероятность появления события A при независимых испытаниях. Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний.

Схема Бернулли состоит в следующем: производится последовательность испытаний, в каждом из которых вероятность наступления определенного события А одна и та же и равна р. Испытания предполагаются независимыми (т.е. считается, что вероятность появления события А в каждом из испытаний не зависит от того, появилось или не появилось это событие в других испытаниях). Наступление события А обычно называют успехом, а ненаступление - неудачей. Обозначим вероятность неудачи q=1-P(A)=(1-p). Вероятность того, что в n независимых испытаниях успех наступит ровно m раз, выражается формулой Бернулли:

Вероятность Р_n(m) при данном n сначала увеличивается при увеличении m от 0 до некоторого значения m₀, а затем уменьшается при изменении m от m₀ до n. Поэтому m₀, называют наивероятнейшим числом наступлений успеха в опытах. Это число m₀, заключено между числами np-q и np+p (или, что то же самое, между числами n(p+1)-1 и n(p+1)) .Если число np-q - целое число, то наивероятнейших чисел два: np-q и np+p. Важное замечание. Если np-q< 0, то наивероятнейшее число выигрышей равно нулю.

Локальная теорема Муавра-Лапласа

Пусть 0< p <1 и величина при n ® ограничена. Тогда .

На практике приближением Муавра-Лапласа пользуются при npq > 9.

Точность формулы растет, как с ростом величин n и k, так и по мере приближения величин p и q к 0.5.

 

Интегральная теорема Муавра-Лапласа

 

Пусть 0< p <1, тогда для схемы Бернулли при n ® для любых a и b справедлива формула

.

Отсюда, в частности, следует, что для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k₁ и k₂, можно использовать формулу

,

где , , - функция Лапласа.

Точность этой приближенной формулы растет с ростом n.

Если npq сравнительно невелико, то лучшее приближение дает формула

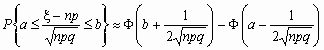
и для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k₁ и k₂, можно использовать формулу

, где , .

5.

6. Дискретные случайные величины.

Рассмотрим дискретную случайную величину (ДСВ) с возможными значениями . Каждое значение возможно, но не достоверно. Величина может принять каждое значение с некоторой вероятностью.

В результате опыта ДСВ примет одно из этих значений, которые несовместны и образуют полную группу.

Простейшая форма задания значений случайной величины и соответствующих вероятностей – это таблица, которая называется ряд распределения ДСВ .

X			
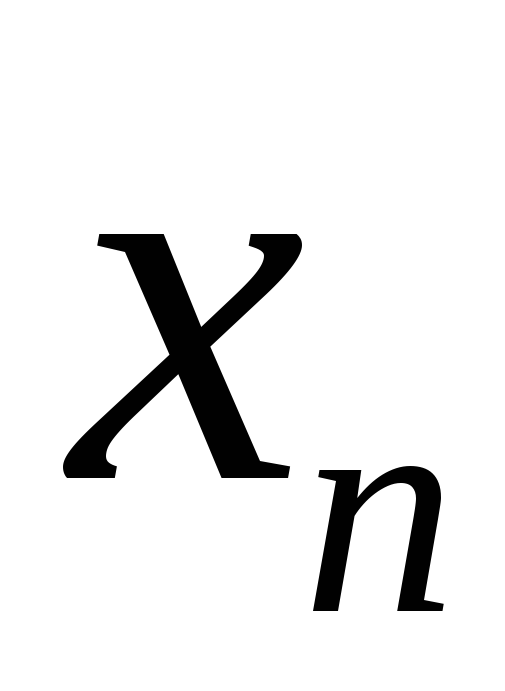
p			

Для наглядности можно по оси абсцисс отложить значения случайной величины, а по оси ординат соответствующие вероятности и соединить полученные точки.

Мы получили многоугольник распределения случайной величины.