
- •35. Постановка задач оптимального управления. Фазовые и управляющие переменные. Амплитудные ограничения. Примеры
- •37. Критерии качества управления. Типы критериев качества
- •38. Классификация задач оптимального управления по типу ограничений фазовые переменные.
- •39. Распространенные задачи оптимального управления. Основные проблемы теории управляемых процессов.
- •40. Принцип максимума л.С. Понтрягина в теории оптимальных систем
- •41. Метод динамического программирования р. Беллмана
- •42. Применение принципа максимума, как проверочного условия
- •43.Применение принципа максимума для сведения задачи оптимального управления к решению двухточечной краевой задачи.
- •45. Принцип максимума л.С. Понтрягина для задач Больца, Лагранжа
- •46. Принцип максимума л.С. Понтрягина для задач терминального управления
- •48. Свойства функции Гамильтона. Достаточность принципа максимума для линейных систем
- •47.Задачи синтеза оптимального управления по быстродействию
- •24. Процесс управления и требования к нему. Итд
40. Принцип максимума л.С. Понтрягина в теории оптимальных систем
Рассмотрим терминальную задачу оптимального управления
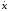 =f(x,
u, t), t0 ≤ t ≤ t1, x(t0) = x0, (12.5.1)
=f(x,
u, t), t0 ≤ t ≤ t1, x(t0) = x0, (12.5.1)
u(t) U
U Er.
(12.5.2)
Er.
(12.5.2)
J(u) =(x(t1)) → min. (12.5.3)
J(u*)
=
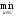 J(u).
J(u).
Предположим,
что вектор-функция f(x, u, t) непрерывна
по своим аргументам вместе с частными
производными
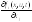 (i,j =1,…,n). U – произвольное ограниченное
множество. В частности, сюда входит
случай замкнутого множества. Функцию
(x)
будем считать непрерывной вместе с
частными производными
(i,j =1,…,n). U – произвольное ограниченное
множество. В частности, сюда входит
случай замкнутого множества. Функцию
(x)
будем считать непрерывной вместе с
частными производными
 (i = 1,…,n).
(i = 1,…,n).
Справедлива следующая теорема.
Теорема 12.1. (Принцип максимума Л.С. Понтрягина).
Пусть u*(t) оптимальное управление в задаче оптимального управления (12.5.1)-(12.5.3), x*(t), ψ*(t) – решение исходной и сопряженной систем, соответствующих оптимальному управлению
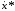 =
f(x*, u*, t), x*(t0)=x0,
=
f(x*, u*, t), x*(t0)=x0,
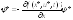 ,
,
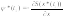 .
.
Тогда в любой момент времени t0 ≤ t ≤ t1 выполняется следующее условие максимума функции H
H(x*(t),
ψ*(t), u*(t), t) =
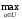 H(x*(t),
ψ*(t), u, t), t0 ≤ t ≤ t1, (12.5.4)
H(x*(t),
ψ*(t), u, t), t0 ≤ t ≤ t1, (12.5.4)
U – произвольное ограниченное множество r-мерного пространства управляющих воздействий. Рассмотрим случай открытой и выпуклой области.
Следствие 1. (Принцип максимума в случае открытой области управления).
Пусть
U открытая область r-мерного пространства.
U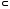 Er
(или оптимальное управление u*(t) проходит
по внутренним точкам множества U,
u*(t)
Er
(или оптимальное управление u*(t) проходит
по внутренним точкам множества U,
u*(t) int
int U)
и правая часть системы вектор-функция
f(x, u, t) дважды дифференцируема по
управлению u. Тогда вдоль оптимального
управления u*(t) выполнено условие
U)
и правая часть системы вектор-функция
f(x, u, t) дважды дифференцируема по
управлению u. Тогда вдоль оптимального
управления u*(t) выполнено условие
 =
0, t0 ≤ t ≤ t1, (12.5.5)
=
0, t0 ≤ t ≤ t1, (12.5.5)
Условие (12.5.5) называется условием стационарности функции H.
Из условия максимума (12.5.4) также следует, что квадратичная форма с матрицей вторых частных производных от функции H должна быть неположительно определенной.
 ≤ 0,
t0 ≤ t ≤ t1, (12.5.6)
≤ 0,
t0 ≤ t ≤ t1, (12.5.6)
η – произвольный вектор размерности r: η ={η1,…, ηr}.
Условие (12.5.6) носит название условия Лежандра-Клебша. Необходимые условия (12.5.5), (12.5.6) являются классическими необходимыми условиями оптимальности известными в вариационном исчислении.
Следствие 2. (Дифференциальный или линеаризованный принцип максимума) Пусть U – выпуклое замкнутое ограниченное множество. Тогда
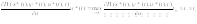 .
.
Определение 12.1. Назовем некоторое допустимое управление u(t), управлением, удовлетворяющим принципу максимума, если вдоль него выполнено условие
 ,
,
где х(t) и ψ(t) решение, исходной и сопряженной систем, соответствующих управлению u(t).
Тогда смысл теоремы 12.1. сводится к утверждению:
Для оптимальности допустимого управления, необходимо, чтобы оно удовлетворяло принципу максимума.
41. Метод динамического программирования р. Беллмана
Принцип
оптимальности:
Оптимальное управление u*(t) обладает
тем свойством, что каково бы ни было
начальное состояние x0
и момент времени t0
≤
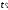 ≤
t1,
управление u*(t),
рассматриваемое на отрезке
≤
t1,
управление u*(t),
рассматриваемое на отрезке
 ≤
t
≤ t1
,оптимально по отношению к полученному
состоянию x*(
≤
t
≤ t1
,оптимально по отношению к полученному
состоянию x*( )
(Ри. 12.3).
)
(Ри. 12.3).
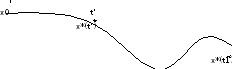
Рис. 12.3. Принцип оптимальности Р. Беллмана
Оптимальное
решение задачи на втором отрезке [ ,
t1]
будет совпадать с решением u*(t).Не
для всяких функционалов справедлив
этот принцип. Для функционала Больца
этот принцип справедлив. Из принципа
оптимальности вытекает следующее
правило для нахождения оптимального
управления:
,
t1]
будет совпадать с решением u*(t).Не
для всяких функционалов справедлив
этот принцип. Для функционала Больца
этот принцип справедлив. Из принципа
оптимальности вытекает следующее
правило для нахождения оптимального
управления:
Каково
бы ни было управление на начальном
отрезке управления [t0, ] (какова бы ни была предистория процесса),
управление на отрезке [
] (какова бы ни была предистория процесса),
управление на отрезке [ ,
t1]
необходимо выбирать оптимальным по
отношению к полученной точке x(
,
t1]
необходимо выбирать оптимальным по
отношению к полученной точке x( ).
).
В результате применяем идею задачи синтеза. Метод динамического программирования позволяет решить задачу синтеза. В соответствии с общей идеей метода динамического программирования вложим задачу (12.6.1)-(12.6.3) в семейство однотипных задач следующего вида:
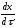 =
f
(x,
u,
τ),
x(t)=x,
=
f
(x,
u,
τ),
x(t)=x,
х
– произвольная точка фазового
пространства.
u(τ) U,
t
≤ τ
≤ t1,
Jx,t(u)
= (x(t1))
+
U,
t
≤ τ
≤ t1,
Jx,t(u)
= (x(t1))
+
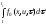 .
.
Значение функционала зависит от начальной точки x и начального момента t. Введем в рассмотрение функцию:
S(x,
t)
=
 Jx,t(u).
Jx,t(u).
Эта функция будет зависеть от начальных значений x, t, S(x, t) – называется функцией Беллмана.
Предположим,
что S(x,
t)
непрерывна для всех x X,
t
X,
t [t0,
t1]
вместе с частными производными
[t0,
t1]
вместе с частными производными
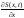 ,
,
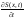 .
Т.е. предполагаем, что функция Беллмана
достаточно гладкая (обладает непрерывными
частными производными). Тогда справедливо
следующее дифференциальное уравнение
в частных производных для функции S(x,
t):
.
Т.е. предполагаем, что функция Беллмана
достаточно гладкая (обладает непрерывными
частными производными). Тогда справедливо
следующее дифференциальное уравнение
в частных производных для функции S(x,
t):
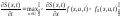 , (12.6.4)
, (12.6.4)
Граничные условия:S(x, t1) = (x).
Дифференциальное уравнение (12.6.4) называется уравнением Беллмана.
Теорема 12.2.(Достаточные условия оптимальности)
Пусть функция u*(x, t) удовлетворяет условию
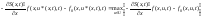 ,
,
где
S(x,
t)
есть гладкое решение уравнения Беллмана
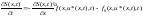 ,
,
S(x, t1) = (x).
Тогда управление u*(x, t) является оптимальным в исходной задаче оптимального управления (12.6.1)-(12.6.3) и
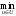 J(u)
= S(x0,
t0).
J(u)
= S(x0,
t0).
С
помощью метода динамического
программирования решается более общая
задача оптимизации – задача синтеза
оптимального управления, поскольку
оптимальное управление находится в
форме синтезирующей функции
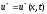 .
Это довольно сложная задача особенно
при большой размерности вектора x.
Основным ограничением является
размерность задачи. Если n3,
то метод динамического программирования
применим.
.
Это довольно сложная задача особенно
при большой размерности вектора x.
Основным ограничением является
размерность задачи. Если n3,
то метод динамического программирования
применим.
Рассмотрим один из возможных способов решения уравнения Беллмана (12.6.4).
Предположим,
что найдено управление
 (x,
(x,
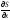 ,
t),
которое максимизирует правую часть
уравнения Беллмана, т.е.
,
t),
которое максимизирует правую часть
уравнения Беллмана, т.е.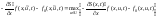 .
.
В
результате приходим к замкнутому
уравнению в частных производных: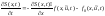 ,
,
S(x, t1)=S(x).
Из
краевого условия вытекает, что
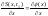 .
.
Рассмотрим
уравнение Беллмана в конечный момент
времени t1:
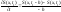
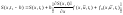 .
.
Все выражения вычисляются при t = t1. Выражение в правой части есть известная функция фазовой переменной x.
S(x, t1) = (x).
Таким образом, найдено значение S(x, t1 - h).
Далее процедура вычислений повторяется. Находим S(x, t1 - 2h), сдвинемся на шаг t1 - h, t1 - 2h и т.д., пока не дойдем до точки t0.
Тогда
управление
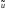 =
= (x,
(x,
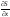 ,
t)
= u*(x,
t)
является оптимальным синтезирующим
управлением, определенным в точках t0,
t0+h,
…, t1.
В результате получим приближенное
решение задачи синтеза.
,
t)
= u*(x,
t)
является оптимальным синтезирующим
управлением, определенным в точках t0,
t0+h,
…, t1.
В результате получим приближенное
решение задачи синтеза.
Можно проводить разбиение и и по фазовой области.
Пример
1. Требуется
минимизировать функционал I=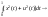 mi
при
условиях
mi
при
условиях 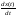 =x+u,
x(0)=1.
=x+u,
x(0)=1.
Решение.
Запишем уравнение Беллмана  .
.
Уравнение
Беллмана конкретизируется в виде 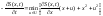 .
.
Необходимо
найти управление, минимизирующее правую
часть уравнения Беллмана при произвольных
x,
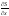 ,
t:
,
t:
 (x,
(x,
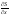 ,
t).
Обозначим p=
,
t).
Обозначим p=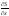 .
.
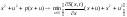
Т.к. левая часть представляет собой параболу с ветвями, направленными вверх, то решение этой задачи единственно и получается из условия равенства 0 первой производной по u от левой части. Это приводит к уравнению 2u+p=0.
Т.е.
u=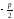 .
.
В
результате уравнение Беллмана
конкретизируется следующим образом: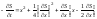 .
.
После
элементарных преобразований уравнение
Беллмана принимает вид: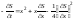 . (12.6.5)
. (12.6.5)
Начальное условие в данном случае имеет вид S(x, t) = 0. (12.6.6)
Таким образом, для нахождения функции Беллмана мы получили задачу Коши (12.6.5), (12.6.6) для нелинейного уравнения с частными производными первого порядка. Будем искать функцию S в виде
S(x, t) = q(t) x2, (12.6.7)
где q(t) – неизвестная функция, удовлетворяющая пока лишь условию:
q(1) = 0, (12.6.8)
что обеспечивает выполнение требования (12.6.6). Подставим теперь (12.6.7) в (12.6.5). Тогда получим
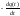 x2
= x2+2x2
q(t)
–
x2
= x2+2x2
q(t)
–
 .
.
Сокращая на x2, находим дифференциальное уравнение для неизвестной функции q(t)
 =
1+2q(t)
– q2(t), (12.16.9)
=
1+2q(t)
– q2(t), (12.16.9)
которое должно решаться при дополнительном условии (12.6.8).
В уравнении (12.16.9) переменные разделяются
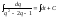 . (12.6.10)
. (12.6.10)
Т.к.
нам надо удовлетворить (12.6.8), то правую
часть в (12.6.10) удобно выразить в виде
(–(1–t)+С).
Левый интеграл в (12.6.10) вычисляется на
основе известных правил интегрирования
рациональных дробей. Полином знаменателя
имеет два вещественных корня q1,2
= 1±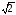 ,
так что дробь под интегралом разлагается
на элементарные следующим образом.
,
так что дробь под интегралом разлагается
на элементарные следующим образом.
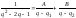 ,
,
где для постоянных А и В имеем систему алгебраических уравнений:
A+B=0,
A2 q2 + B1 q1 = –1,
решение которой B = –A, A = –1/(q1– q2).
Учитывая
значение корней q1,
q2
получимА =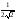 ,
В = –А.
,
В = –А.
Тогда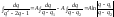 .
.
После
этого (12.6.10) переписывается так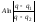 = – (1– t)+C.
= – (1– t)+C.
Отсюда
с учетом, того что А-1
= 2 ,
,
Получаем
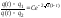 . (12.6.11)
. (12.6.11)
Константа С находится из условия (12.6.8), для этого надо положить в (12.6.11) t = 1, q(1)= 0, что дает С = q1/q2. Подставив данное выражение в (12.6.11) и разрешив относительно q(t) имеем
 .
.
После
этого оптимальный синтез вычисляется
по формуле u*(x,
t)
= –0.5 ,что
дает u*(x,
t)
= –q(t)
x.
,что
дает u*(x,
t)
= –q(t)
x.
Приведенная в данном примере техника решения уравнения Беллмана распространяется на т.н. линейно-квадратичный класс задач оптимального управления, в котором управляемый процесс описывается произвольной линейной системой (по x и u), а критерий оптимальности представляет собой интеграл от положительно определенной квадратичной формы. Этот класс нашел свое приложение в ряде задач механики и физики.
