1. Управление представляет собой процесс выработки и осущ-ия управляющего воздействия по переводу объекта в желаемое состояние. Под объектом управления понимается объект, для достижения желаемых результатов функционирования которого необходимы и допустимы специально организованные воздействия. Объектами управления могут быть как отдельные объекты, выделенные из окружающего нас мира (среды) по опред-ным признакам, так и совокупности объектов – комплексы. В зависимости от свойств или назначения объектов управления могут быть выделены технические, технологические, экономич-ие, организационные, социальные и другие объекты управления и комплексы. Объект управления выделяется из окружающей среды таким образом, чтобы выполнялись, по меньшей мере, два условия:

-на объект можно воздействовать;

-это воздействие может приблизить нас к осуществлению поставленных целей в объекте, т.е. изменить его состояние в желаемом для нас направлении. Под целью управления подразумевается совокупность условий, свойств, требований, которым должен удовлетворять объект управления.

Назовем системой управления такую совокупность объекта управления и управляющего устройства, процесс взаимодействия которых приводит к выполнению поставленной цели управления.

Признаки классификации	Принципы управления
Степень исп-ия при упр-ии инф-ии о событиях упр-я	С обратной связью; без обратной связи
Степень исп-ия при упр-ии инф-ии о возмущениях	По возмущениям; комбинированные
Степень использования при управлении информации о параметрах и структуре объекта управления	Адаптивное (беспоисковое, поисковое, с идентификацией); с переменной структурой; неадаптивное
Степень опред-сти преобр-ий координат в СУ	Детерминированное; стохастическое
Вид мат-кой модели преобр-ий координат в сист. Управления	Линейное; нелинейное (релейное, логическое и др.)
Вид управляющих воздействий	Аналоговое (непрерывное); дискретное (прерывистое, импульсное, цифровое)
Степень участия в управлении человека – оператора	Ручное; автоматическое; автоматизированное (человек - оператор)

Разомкнутые САУ – это системы, в которых выход ОУ не подается на вход УУ, т.е. нет контроля за состоянием ОУ. Разомкнутыми такие системы называются также потому, что в них отсутствует обратная связь между выходом ОУ и входом УУ, при наличии которой ОУ и УУ образуют замкнутый контур. Возможны разомкнутые САУ, в которых УУ измеряет только задающее воздействие g, только возмущение f и, наконец, оба эти сигнала одновременно. Первый вариант разомкнутой САУ называется САУ по задающему воздействию. Второй вариант называется САУ по возмущению, или системой автоматической компенсации. САУ по задающему и возмущающему воздействиям является наиболее полным видом разомкнутой САУ.

В замкнутых САУ на вход УУ подаются задающее воздействие g и выходная величина y. Исходя из величины g, УУ определяет соответствующее требуемое значение y, и на основе информации о текущем значении y обеспечивает необходимое соответствие между y и g путем воздействия на ОУ. В такой САУ УУ стремится ликвидировать все отклонения выхода ОУ от его значения, определяемого заданием для цели управления, независимо от причин, вызвавших это отклонение, включая любые возмущения, внешние и внутренние помехи, а также изменения параметров системы. САУ такого типа представляет собой замкнутый контур, образованный ОУ и УУ. При этом УУ создает обратную связь вокруг ОУ, связывая его выход со входом, поэтому замкнутые САУ называют еще системами с обратной связью или системами управления по отклонению. Это основной тип САУ.

Есть еще и комбинированные САУ, которые представляют собой объединение в одну систему замкнутой системы управления по отклонению и разомкнутой системы управления по внешнему воздействию.

Схема на рис. 1.4 является схемой такой комбинированной САУ. Комбинированные САУ обладают лучшими характеристиками. В них наиболее полно используется информация об ОУ и внешней ситуации.

2. На рис. 1.5 приведена более полная по сравнению с рис. 1.4 типовая функциональная схема САУ, на которой показаны основные составные части управляющего устройства: ЧУ, ВУ, ИУ.

Рис. 1.5– Типовая функциональная схема САУ

Чувствительные устройства (ЧУ) (измерительные устройства, датчики) служат для измерения подаваемых на управляющее устройство воздействий (сигналов) f, g, y.

Вычислительное устройство (ВУ) реализует алгоритм работы управляющего устройства. В простейшем случае оно осуществляет элементарные математические операции, такие, как операция сравнения, определяющая разность g – y, т.е. сравнение цели управления и выхода объекта управления. Используются также операции интегрирования, дифференцирования и т.п. В более сложных случаях ВУ может представить собой ЭВМ и даже комплекс ЭВМ.

Исполнительное устройство (ИУ) – предназначено для непосредственного управления объектом, т.е. изменения его состояния в соответствии с сигналом, выдаваемым ВУ.

Вышеперечисленные составные части являются основными, но, кроме них, могут быть и другие вспомогательные устройства, например преобразователи, служащие для согласования отдельных частей системы, устройства связи и т.п.

3. Рассмотрим классификацию САУ по ряду признаков, существенных с точки зрения теории управления.

Многие САУ создаются на основе комплексирования нескольких принципов управления, поэтому допустимы составные определения, например цифровое управление с идентификацией.

САР – это САУ, задачей которой является поддержание выходной величины ОУ y на заданном уровне g, т.е. поддержание равенства y = g. В зависимости от характера задающего воздействия САР делятся на три вида:

-системы автоматической стабилизации, задающий сигнал в которых g(t) = const, а выходной параметр САУ поддерживается на уровне заданного значения (y(t) = const);

-системы программного управления, задающий сигнал в которых g(t) зависит от известной задающей программы (например, числовое программное устройство управления станком);

-следящие системы, изменение задающего сигнала в которых происходит по неизвестному закону, заданному тем или иным способом.

По виду зависимости регулируемой величины от внешнего воздействия различают статические и астатические САУ:

статические САУ – это системы, в которых при возмущающем воздействии регулируемая величина y(t) по окончании переходного процесса принимает значения, пропорциональные возмущающему воздействию. В этих системах статическое звено САУ имеет между выходной и входной величинами строго определенную функциональную связь, которую принято называть статической характеристикой y = F(x); астатические САУ – это системы, в которых при внешнем воздействии f и окончании переходного процесса значение регулируемой величины устанавливается равным заданному, т.е. в установившемся режиме разность между заданным и текущим значениями регулируемой величины равна нулю.

По виду воздействия регулирующего органа (или ИЭ, УУ) на объект управления, т.е. по виду управляющих воздействий, различают непрерывные и дискретные системы.

В системах непрерывного аналогового управления между выходной и входной величинами существует определенная непрерывная функциональная связь y = F(g), где F является аналитической непрерывной функцией. В общем случае непрерывной динамической системы F представляет собой оператор системы, частными случаями которого являются функционал и функция. В системах прерывистого (дискретного) управления функция (оператор) F(g) является дискретной. Эти системы, в свою очередь, подразделяются на системы релейного действия, импульсные и цифровые системы.

В системах релейного действия в структуре САУ имеются один или несколько релейных элементов (РЭ – элементов порогового действия, типа 0,1).

Импульсные САУ характеризуются наличием импульсного элемента, выходная величина которого представляет собой последовательность импульсов. Один из параметров импульса (амплитуда, длительность, момент начала действия импульса) является функцией входной величины.

Существует много модификаций импульсных САУ, различающихся по принципу модуляции входного сигнала: временно-импульсные, широтно-импульсные, амплитудно-импульсные и САУ с комбинацией этих модуляций.

Цифровые САУ – это САУ, контур управления которых для реализации алгоритмов управления содержит ЭВМ или цифровые вычислительные устройства.

Системы комбинированного типа: аналого-дискретные, дискретно-аналоговые или аналого-цифровые, цифро-аналоговые – представляют собой смешанную реализацию рассмотренных выше структур.

4. По характеру звеньев, включаемых в САУ, системы делятся на линейные и нелинейные.

В линейных системах между выходной и входной величинами существует линейная функциональная зависимость (в статическом и динамическом режимах работы).

Процессы, происходящие в этих системах, описываются линейными дифференц. уравнениями.

Для линейных систем всегда выполняется принцип суперпозиции. Для нелинейных систем он не выполняется. Принцип суперпозиции заключается в следующем.

Пусть y(t) = A_ix(t), тогда, если

то

Нелинейной системой называется такая система, в которой хотя бы в одном звене нарушается линейность статической характеристики или же имеет место любое другое нарушение линейности уравнений динамики этого звена. Например, произведение переменных или их производных, корень, квадрат или более высокая степень переменной, любая другая нелинейная связь переменных или их производных.

Все реальные САУ обычно являются нелинейными, но САУ с несущественной нелинейностью характеристик линеаризуют. Несущественно нелинейные характеристики не содержат разрывов непрерывности. Существенно нелинейные характеристики содержат изломы, разрывы непрерывности первого рода и т.д. Теория линейных САУ в настоящее время полностью разработана, поэтому целесообразно сводить там, где это возможно, нелинейные САУ к линейным, используя методы линеаризации. Однако нелинейные САУ богаче по своим возможностям, в том числе и в смысле улучшения качества процессов управления.

5. В зависимости от вида дифференц. уравнения линейные системы подразделяются на следующие типы:

1) Обыкновенные САУ, описываемые обыкновенными линейными дифференц. уравнениями (уравнениями типа вход-выход):

2) САУ с распределенными параметрами, описываемые дифференциальными уравнениями в частных производных, например:

где x – пространственная координата.

3) САУ с запаздыванием, описываемые линейными дифференциальными уравнениями с запаздыванием:

где  - время чистого запаздывания.

4) САУ с переменными параметрами, коэффициенты в уравнениях которых зависят от времени. Такие системы называются также нестационарными системами и описываются, например, уравнениями следующего вида:

Если a_i = const, т.е. параметры системы постоянны, то она называется стационарной. При a_i = a_i(t) САУ называются нестационарными.

Стационарной называется система, реакция которой на любой тип возмущения зависит только от интервала между данным моментом времени и моментом начала возмущения.

6. принцип суперпозиции. Принцип суперпозиции заключается в следующем.

Пусть y(t) = A_ix(t), тогда, если

то

7. По степени использования при управлении информации о параметрах и структуре ОУ САУ делятся на адаптивные и неадаптивные. Адаптивные (самоприспосабливающиеся) системы обладают способностью приспосабливаться к изменению внешних условий, а также улучшать свою работу по мере накопления опыта.

Неадаптивные системы такой способностью не обладают. Они имеют постоянную настройку. Если вследствие какого-либо изменения условий работы такой системы ее настройку требуется изменить для того, чтобы сохранить заданное качество управления (н-р, точность, быстродействие), это должен сделать человек.

Область применения адаптивных САУ – это управление объектами, свойства и условия работы которых недостаточно известны или существенно непостоянны. В этих условиях неадаптивная система либо будет работать неудовлетворительно, либо потребует постоянного надзора.

Адаптивные САУ в свою очередь различаются по степени самонастройки, адаптации, оптимизации и интеллектуализации.

Экстремальные системы (системы с самонастройкой программы) – это САУ, в которых значение регулируемой величины y(t) автоматически поддерживается на экстремальном значении (максимум, минимум) при различных значениях неизвестных возмущающих воздействий f(t) (рис. 1.6). Программа изменения y(t) определяется автоматически в процессе работы САУ. В САУ добавлено специальное устройство автоматического поиска экстремума (УАПЭ), которое на основе анализа определенных характеристик ОУ (z) выдает на вход САУ воздействие g₃(t). В результате УУ (регулятор) вырабатывает управляющее воздействие u(t), определяющее оптимальное поведение САУ при изменении y(t), например поддержание работы САУ на экстремальном значении y=y_max.

ос

Рис. 1.6 – Функциональная схема экстремальной системы

Обычно при проектировании САУ всегда преследуют экстремальную цель управления. Экстремальные системы по существу являются системами автоматической стабилизации выходной величины y=y_extr или экстремума некоторого функционала . В последнем случае САУ решают не только задачу экстремального управления, но и задачу оптимизации, т.е. являются оптимальными САУ.

Системы с самонастройкой параметров (самонастраивающиеся системы) – это системы, в которых автоматически в зависимости от заранее неизвестных внешних условий (по f, g) устанавливаются оптимальные значения параметров системы. Следовательно, УУ работает таким образом, чтобы регулируемая величина на выходе САУ изменилась по наивыгоднейшему (оптимальному) закону в соответствии с априори заданным критерием качества – функционалом J. Под функционалом J могут рассматриваться сложные функции полезности, максимума прибыли, минимума потерь или минимума расхода энергии при работе САУ и т.п. В роли J могут быть использованы простые оценки качества процессов, например: минимум длительности переходного процесса t_n=min или минимум среднеквадратичной ошибки управления x²=min и т.п.

Рис. 1.7 – Функциональная схема самонастраивающейся САУ

В схему самонастраивающейся САУ (рис. 1.7) входит устройство самонастройки (УСН) – анализатор качества или оптимизатор, который определяет отклонение характеристик замкнутой САУ от желаемых (эталонных) и в зависимости от состояния системы – некоторой функции F(x,g,z,y) – воздействует на УУ. Следовательно, такие системы – это системы с самооптимизацией или иначе, адаптивные САУ со стабилизацией качества (оптимальные по быстродействию, по точности, по технико-экономическим показателям и т.п.).

Системы с самонастройкой структуры называются также самоорганизующимися или самоалгоритмизирующимися системами, в которых в зависимости от неопределенных внешних условий производится оптимальная настройка структуры таким образом, чтобы регулируемая величина на выходе изменилась по наивыгоднейшему (оптимальному) закону в соответствии с заданным критерием качества J (в простейшем случае, например, минимум ошибки управления). Автоматический поиск наивыгоднейшей (оптимальной) структуры САУ дает возможность решать более сложные задачи при управлении сложными ОУ – комплексами.

В схеме САУ с самонастройкой структуры (рис. 1.8) идентификатор производит сбор и обработку информации о работе ОУ. САУ строится как система принятия решений об управлении сложным ОУ.

Рис. 1.8 – Схема САУ с самонастройкой структуры

Системы комбинированного типа с самонастройкой структуры и параметров объединяют в своем составе определенные фрагменты рассмотренных выше структур. Все эти САУ являются также и оптимальными САУ.

В последние два десятилетия интенсивно разрабатывается новый класс САУ, получивший название интеллектуальные системы управления (ИСУ). В связи с возникновением этого класса САУ отметим, что в классическом понимании САУ, включающие разнообразные ОУ, воспринимались как системы, процессы в которых принципиально прогнозируемы и управляемы. Ошибки в управлении и неработоспособность систем часто рассматривались как недостаток априорных знаний (обычно об ОУ). Наращивание объема знаний в процессе эксплуатации САУ (принцип обучения и самообучения) привело к созданию обучающихся адаптивных САУ с гибкими алгоритмами управления (в том числе и процедурами принятия решений) и идентификации ОУ. Обучающиеся адаптивные САУ – это системы с накоплением, запоминанием и анализом информации о поведении сложного ОУ, среды функционирования и САУ в целом с изменением алгоритмов управления в зависимости от опыта и условий работы. Логика развития подобных проблем определила создание ИСУ, которые строятся как самообучающиеся, самонастраивающиеся системы с гибкими процедурами принятия решений об управлении, как системы, основанные на знаниях и формирующие новые знания в процессе управления и функционирования. ИСУ разрабатываются и как экспертные системы, встроенные в контур управления и работающие, в частности, в интерактивном режиме с лицом, принимающим решение.

8. При создании САУ одной из первоочередных задач, является математическое описание системы. Математическое описание (построение математической модели САУ) сопровождается разбиением системы на звенья и описанием этих звеньев. Совокупность описаний (уравнений, характеристик) отдельных звеньев определяет математическое описание или характеристики системы в целом.

При изучении принципа действия САУ рассматривалась ее функциональная схема, в которой САУ разбита на звенья исходя из их назначения. При математическом описании САУ разбивают на звенья по другому принципу: исходя из удобства получения этого описания. Для этого систему разбивают на возможно более простые «мелкие» звенья направленного действия, которые передают воздействия только в одном направлении – от входа на выход. При этом предполагается, что изменение состояния такого звена не влияет на состояние предшествующего звена, работающего на его вход. Именно поэтому при разбиении САУ на звенья направленного действия математическое описание каждого звена может быть составлено без учета его связей с другими звеньями. Соответственно математическое описание всей системы в целом может быть получено как совокупность составленных независимо друг от друга математических описаний или характеристик отдельных звеньев, дополненных уравнениями связей между звеньями. При этом целесообразно, чтобы каждое звено в динамике описывалось дифференциальным уравнением не выше второго порядка.

Независимое математическое описание звеньев позволяет легко составить структурную схему системы. Структурная схема системы состоит из прямоугольников, изображающих звенья системы, и стрелок, соединяющих входы и выходы звеньев. Стрелки показывают не только связи между звеньями, но также и внешние воздействия, приложенные к отдельным звеньям системы. Каждому звену структурной схемы придается описывающее его уравнение или характеристика. Обычно эта характеристика или уравнение записывается прямо внутри прямоугольника, изображающего звено. Структурная схема определяет основу математического описания САУ.

9. Динамические свойства линейных звеньев САУ в целом могут быть описаны либо аналитически в виде уравнений, связывающих выходные и входные величины звена, либо графически в виде характеристик, описывающих ту же связь.

В ТАУ применяются два типа таких характеристик: временные (переходные) и частотные.

Характеристики могут быть рассчитаны и построены по уравнению звена или сняты экспериментально. По экспериментально полученным характеристикам можно составить уравнение звена. С помощью этик характеристик можно определить реакцию на любое воздействие (возмущение) произвольного вида, так как для линейных систем справедлив принцип суперпозиции,

Из этой формулы следует, что если нам известны реакции линейной системы на элементарные (типовые) возмущения, то мы можем определить реакцию линейной системы на любое произвольное воздействие. В ТАУ применяются два вида типовых воздействий: типовые функции времени; типовые гармонические сигналы. На основе типовых функций времени определяются временные (переходные) характеристики, а на основе типовых гармонических сигналов – частотные характеристики. Таким образом, временные (переходные) и частотные характеристики однозначно связаны с уравнением звена (САУ) и наряду с ним является исчерпывающим описанием динамических свойств звена (САУ).

10. Из типовых функций времени наиболее часто используются две: единичная импульсная функция и единичная ступенчатая функция.

Единичной импульсной функцией (дельта-функцией, -функцией) называется функция, равная нулю всюду, кроме начала координат, принимающая бесконечное значение в начале координат и притом так, что интеграл от нее по любому интервалу, содержащему начало координат, равен единице: (t) = 0, t  0; (0) = ;

Функцию, обладающую такими свойствами, можно получить, например, как предел положительного импульса, имеющего единичную площадь, когда длительность этого импульса   0. Еще удобнее определить -функцию как предел функции при h  .

Практически удобно еще требовать, чтобы -функция была четной. Тогда, ,

при любом  > 0. Важным является то, что для любой непрерывной функции x(t):

Т.е. интеграл от произведения -функции на любую непрерывную функцию равен значению этой функции при том значении переменной интегрирования, при котором аргумент -функции обращается в нуль. Выражение можно переписать в более общем виде, для любого интервала (a, b), содержащего точку t, т.е. a < t < b:2.3.4

Действительно, формула (2.3.4) представляет функцию x(t) в виде суммы бесконечно большого числа бесконечно малых слагаемых вида x()(t-)d. Каждое такое слагаемое представляет собой бесконечно малый импульс x()d, действующий в момент времени t = , так как (t-) по определению является мгновенным единичным импульсом, действующий в момент времени t = .

Если функция x(t) задана при всех значениях t, и мы хотим представить ее разложением на элементарные импульсы на всей числовой оси, то, приняв в (2.3.4) a = - , b = , получим: форм.2.3.5

Пусть на вход линейной системы, описываемой оператором А_t (рис. 2.3), поступает сигнал x(t), тогда выходная величина этой системы равна y(t) = A_tx(t)

y(t) x(t)

Рис. 2.3. Оператор линейной системы

Подставим в эту формулу выражение (2.3.5) и проведем преобразование на основе (1.9.1):

. (2.3.7)

Формула (2.3.7) показывает, что для нахождения реакции линейной системы на произвольное возмущение x(t) достаточно знать ее реакцию на единичный импульс (t-), действующий на нее в произвольный момент времени .Эта реакция зависит от переменных t и , т.е. от момента действия импульса  и текущего момента времени t:.(2.3.8)

Функция , определяемая формулой (2.3.8), является исчерпывающей характеристикой линейной системы и называется ее весовой или импульсной переходной функцией. Весовая или импульсная переходная функция линейной системы представляет собой реакцию этой системы в момент времени t на единичный импульс, действующий на систему в момент времени .

Следовательно,. (2.3.9)

Таким образом, оператор любой линейной системы может быть представлен в форме линейного интегрального оператора.

Отметим, что физическая система не может реагировать в данный момент времени на возмущение, которое будет действовать на нее позже, т.е..(2.3.10)

Данное условие называется условием физической возможности системы (физической реализуемости системы).

Для физически возможной линейной системы, находящейся в покое до момента времени t₀, имеем

(2.3.11)

11. Во многих задачах практики удобно использовать в качестве типовых воздействий гармонические колебания всех возможных частот. Известно, что при весьма общих условиях любую функцию можно разложить в ряд Фурье или представить интегралом Фурье. Поэтому, зная реакцию линейной системы на гармонические колебания всех возможных частот и пользуясь принципом суперпозиции, мы можем определить реакцию системы на произвольное возмущение.

Рассмотрим некоторую функцию x(t). Если эта функция абсолютно интегрируема, то ее можно представить интегралом Фурье:(2.4.1) где(2.4.2)

Эти формулы определяют преобразование Фурье. Если возмущение x(t) действует на входе линейной системы, описываемой оператором A_t (рис. 2.3), то на основании принципа суперпозиции выходная функция системы равна (2.4.3)

где A_te^it – реакция системы на гармонические колебания частоты .

Реакция системы на гармонические колебания может принята за характеристику линейной системы. Зная эту характеристику, мы можем по формуле (2.4.3) вычислить реакцию линейной системы на произвольное возмущение, которое можно представить рядом или интегралом Фурье. Обычно эту характеристику обобщают и в качестве типового воздействия рассматривают показательную функцию e^pt, где p – произвольный комплексный параметр. Если p – чисто мнимый параметр, т.е. p = i, то e^pt - гармонические колебания частоты , т.к. e^pt = cost + isint. Если р – комплексный параметр с отрицательной действительной частью, то e^pt – затухающие гармонические колебания. Если р – комплексный параметр с положительной действительной частью, то e^pt – расходящиеся гармонические колебания. Если р – действительное число, то e^pt можно рассматривать как затухающие или расходящиеся гармонические колебания нулевой частоты. Таким образом, семейство показательных функций e^pt охватывает гармонические колебания всех возможных частот.

Любая система, которую мы будем возбуждать гармоническими колебаниями, будет реагировать на них также каким-то колебательным движением. Нужно задать такую характеристику, которая определяет преобразование амплитуды и сдвиг фазы выходного колебания по отношению к входному.

Такой характеристикой может быть следующее отношение: (2.4.4)

Функцию W(t,p) называют характеристикой реакции линейной системы на показательное возмущение или параметрической передаточной функцией.

12. В частном случае при чисто мнимых значениях параметра р формула определяет частотную характеристику линейной системы:

. (2.5.1)

Следовательно, частотная характеристика линейной системы есть отношение реакции линейной системы на гармонические колебания единичной амплитуды и частоты  к этой гармонической функции e^it. На основании (2.5.1) реакция линейной системы на гармонические колебания данной частоты  и единичной амплитуды e^it равна произведению значения частотной характеристики системы при данном значении частоты на входную функцию e^it: .

Найдем реакцию линейной системы на входные гармонические колебания произвольной амплитуды а и фазы :

(2.5.2)

Частотная характеристика линейной системы в общем случае является комплексной функцией, поэтому ее можно представить в показательной форме:.(2.5.3)

Подставляя (2.5.3) в (2.5.2), получим:

,

где

Эта формула показывает, что линейная система реагирует на гармонические колебания входной величины в общем случае колебаниями переменной амплитуды b(t) и переменного сдвига фазы (t).

Пользуясь частотной характеристикой линейной системы (2.5.1), можно связь (2.4.3) между выходом и выходом системы записать в следующем виде: . (2.5.4)

Сравнивая формулу (2.5.4) с формулой (2.3.9) видим, что они имеют много общего: за характеристику системы принимается некоторая функция двух переменных (текущего времени и какого-либо параметра). В (2.3.9) в качестве такого параметра принимается момент действия единичного импульса, а в (2.5.4) – круговая частота гармонического колебания . Однако из (2.5.4) следует, что применение частотных характеристик включает лишнюю операцию перехода к преобразованию Фурье. И это будет общей закономерностью.

Какими бы типовыми элементарными воздействиями мы не пользовались, кроме -функции, нужно находить какое-то преобразование входного воздействия, а потом уже определять выходную переменную системы. И только использование в качестве элементарного воздействия -функции дает существенное упрощение, так как при этом исключается необх-сть дополнительного преобразования входного воздействия.

Следовательно, для произвольных линейных систем применение частотных характеристик нерационально. Только для систем с медленно изменяющимися параметрами (т.е. параметры системы можно считать постоянными на значительных промежутках времени) целесообразно использование частотных характеристик.

Именно поэтому частотные характеристики широко используются для исследования стационарных линейных систем.

13. На основании изложенного выше для линейной стационарной системы (2.5.3) перепишется в следующем виде: .(2.6.1)

Эту характеристику называют амплитудно-фазовой частотной характеристикой (АФХ) (в литературе иногда используются выражение «частотная передаточная функция») стационарной линейной системы. Здесь A()=|W(i)| - амплитудная частотная характеристика, а - фазовая частотная характеристика. Из (2.6.1) следует, что частотные характеристики линейной стационарной системы являются функцией одного параметра – частоты гармонических колебаний. Именно этим объясняется широкое использование частотных методов исследования в классический период развития ТАР и ТАУ. Графики амплитудной и фазовой частотных характеристик приведены на рис. 2.4, причем амплитудная частотная характеристика (АЧХ) является четной функцией, т.е. A(-)=A(), а фазовая частотная характеристика (ФЧХ) – нечетной функцией, т.е. (-)=-().

Графически амплитудно-фазовая частотная характеристика изображается на комплексной плоскости (рис. 2.5) в полярных координатах (А, ) как годограф функции W(i).

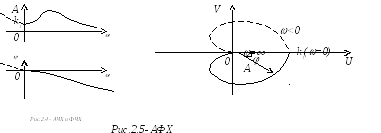
Однако чаще строят амплитудно-фазовую частотную характеристику в прямоугольных координатах (U,V) (рис.2.5), выделив в выражении W(i) вещественную и мнимую части

При этом U() называют вещественной частотной характеристикой, а V() – мнимой.

Угол  показан на рис.2.5 как отрицательный (отложен по часовой стрелке), так как чаще всего реакция на выходе звена имеет отставание по фазе по сравнению с входной величиной. При этом частоту  изменяют от 0 до  (сплошная кривая на рис.2.5) или от -  до + , тогда добавляется еще симметричная к ней пунктирная кривая.

15. На практике чаще всего амплитудную и фазовую частотные характеристики изображают в логарифмическом масштабе.

Построенные таким образом частотные характеристики на­зываются логарифмическими частотными характеристиками.

Логарифмическая амплитудная частотная характеристика (ЛАХ) строится в виде зависимости

L()=20 lg A()=20 lg|W(i)|,

а логарифмическая фазовая частотная характеристика (ЛФХ) строится в виде зависимости () от lg().

В качестве единицы измерения величины L() используют децибел:

1 Б соответствует усилению мощности сигнала в 10 раз, 2 Б – в 100 раз и т.д.

Мощность сигнала пропорциональна квадрату амплитуды: , поэтому усиление в белах, выраженное через отношение амплитуд А, равно. Следовательно, в децибелах оно равно 20lgA.

На оси абсцисс указываются значения [c^-1] Единицей приращения lg является декада, соответствующая изме­нению частоты в 10 раз (иногда используется октава, соот­ветствующая изменению частоты в 2 раза (1 октава равна 0,303 декады, так как)). Начало координат обычно помещают в точке , так как. Точка пересечения ЛАХ с осью абсцисс определяет частоту среза _ср.

Главное достоинство ЛАХ состоит в возможности их по­строения практически без вычислительных работ, например, суммированием или в виде асимптотических ЛАХ (совокупности отрезков прямых линий с наклоном, кратным 20 дБ/дек). Кроме того, в логарифмических координатах уменьшается кривизна ха­рактеристик.

16. Передаточная функция линейной САУ в общем случае оп­ределяется формулой W(t,p)=A_te^pt/e^pt. (2.8.1)

Реакция стационарной линейной системы на по­казательное возмущение не зависит от текущего времени, по­этому из формулы (2.8.1) следует, что для стационарного случая A_te^pt=W(p)e^pt.

Отсюда получим следующее определение: передаточной функцией стационарной линейной системы называется множи­тель, на который умножается показательная функция e^pt, про­ходя через эту систему. Непосредственно из формулы частотной характеристики для стационарной линейной системы следует, что (2.8.2) т.е. передаточная функция стационарной линейной системы яв­ляется преобразованием Лапласа от весовой (импульсной пере­ходной) функции. Для физически возможной стационарной ли­нейной САУ имеем (2.8.3)

Из операционного исчисления известно, что интеграл (2.8.3) является интегралом свертки. Обозначая преобразования Лап­ласа от входной x(t) и выходной y(t) переменных системы со­ответственно через X(p) и Y(p), учитывая (2.8.2), предполагая равенство нулю всех внешних возмущений и нулевые начальные условия, получим из (2.8.3) следующее выражение для переда­точной функции стационарной линейной системы:

Данное описание является наиболее распространенной де­терминированной математической моделью стационарной ли­нейной системы.

19. (2.11.1)

Выражение (2.11.1) формально определяет передаточную функцию стационарной линейной системы, поведение которой описывается дифференциальными уравнениями (2.9.8), при всех значениях р, кроме совпадающих с корнями характеристиче­ского уравнения системы (2.11.2)

Однако физически эта передаточная функция существует не при всех значениях р. В общем случае реакция системы на показательное возмущение представляет собой полное решение уравнения (2.9.8), а не частное. Для получения полного решения уравнения (2.9.8) следует к найденному частному решению доба­вить общее решение соответствующего однородного диффе­ренциального уравнения

(2.11.3)

Из теории дифференциальных уравнений известно, что ес­ли корни характеристического уравнения (2.11.2) v,...,vn все различны, то общее решение уравнения (2.11.3) представляет собой линейную комбинацию показательных функций с произвольными коэффициентами. Если некоторые корни харак­теристического уравнения совпадают, например , то функции заменяются функциями . Таким образом, в случае, когда харак­теристическое уравнение не имеет кратных корней, общее ре­шение уравнения (2.9.8) определяется формулой (2.11.4)

Для определения передаточной функции системы разделим (2.11.4) на ept : (2.11.5)

Если действительные части всех разностей отрицательны, то все показательные функции в (2.11.5) стремятся к 0 при . В этом случае передаточная функция системы, представляющая собой отношение реакции этой системы на бесконечно долго действующее на нее возмущение ерt к самому возмущению ерt, определяется формулой (2.11.1). Если хотя бы одно из чисел имеет по­ложительную действительную часть, то соответствующая пока­зательная функция в (2.11.4) неограниченно возрастает при , и, следовательно, передаточная функция системы не су­ществует.

Таким образом, передаточная функция стационарной линей­ной системы, описываемой дифференциальным уравнени­ем (2.9.8) существует только в области значений р, действи­тельные части которых больше действительных частей всех корней характеристического уравнения (рис.2.5).

Рис.2.5 - Область существования передаточной функции

Очевидно, что частотная характеристика, представляющая собой значение передаточной функции на мнимой оси , существует для рассматриваемой системы только в том случае, когда действительные части всех корней характеристической: уравнения отрицательны. В дальнейшем мы увидим, что эт условие необходимо и достаточно для устойчивости стационар ной линейной системы.

Все виды динамических характеристик линейных систем (дифференциальное уравнение, передаточная функция, частот­ные характеристики, весовая (импульсная переходная) функция, переходная функция) связаны между собой определенными за­висимостями и эквивалентны друг другу в определении динами­ческих свойств системы, поэтому изложенного выше вполне до­статочно для изучения динамических свойств звеньев линейных САУ, описываемых дифференциальными уравнениями.

18. Переменные состояния – это промежуточные переменные системы (рис.2.4), число которых равно ее порядку n. В общем случае u и выходные у переменные могут быть векторными величинами размерности m и l соответственно.

Рис.2.4 – Состояние системы

Переменные состояния называют также координатами состояния, так как их совокупность задает вектор состояния .

Множество возможных положений этого вектора образует векторное пространство Х, называемое пространством состояний системы. В переменных состояния САУ описывается векторно-матричным уравнением

(2.9.9)

где - квадратная матрица коэффициентов (ее называют также собственной параметрической матрицей системы); – входная матрица (матрица управления) системы; – выходная матрица системы; – вектор переменных состояния внутренних координат системы; – вектор входных переменных (управляющих и возмущающих); – вектор наблюдаемых или выходных переменных; размерности матриц А, В, С соответственно .

Процессы в САУ в свободном движении (без внешних воздействий) согласно уравнению (2.9.9) описываются векторно-матричным уравнением с характеристическим уравнени­ем , где Е - единичная матрица, или в раз­вернутом виде системой дифференциальных уравнений

с характеристическим уравнением

(2.9.10)

Эти уравнения при определенных начальных условиях дают возможность изучить процессы в системе путем их решения чис­ленными методами с использованием ЭВМ.

Разработаны различные способы перехода от уравнений типа «вход-выход» к уравнениям состояния вида (2.9.9) и наобо­рот. Один из наиболее распространенных способов состоит в следующем. Пусть САУ описывается уравнением (2.9.1). Введем обозначения

С помощью этих обозначений преобразуем уравнение (2.9.1) к следующему виду:

(2.9.11) где

В нашем примере у и и₁ являются скалярными величина­ми. В общем случае (2.9.9) - это, соответственно, вектор наблю­даемых или выходных переменных и вектор входных перемен­ных (управляющих и возмущающих), поэтому в (2.9.11) матрицы В и С выродились в вектор-столбец и вектор-строку соответст­венно.

Система уравнений (2.9.11) представляет собой описание ли­нейной непрерывной системы в пространстве состояний . Уравнения (2.9.11) с матрицей называют уравнениями в форме Фробениуса. Если , то

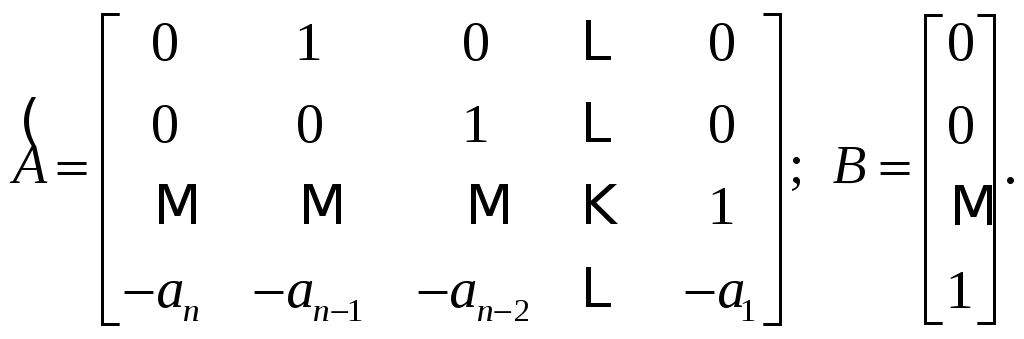
Форма уравнений (2.9.11) с подобными матрицами и В называется в ТАУ канонической формой фазовой переменной.

Для современной ТАУ как математической теории харак­терно то, что в ней важное место занимает исследование прин­ципиальной возможности синтеза алгоритмов оценивания, иден­тификации, управления и адаптации. Эта возможность в значи­тельной степени выявляется при изучении свойств системы, ко­торые принято называть наблюдаемостью, идентифицируемо­стью, управляемостью и адаптируемостью. Заметим, что часто между наблюдаемостью и идентифицируемостью не делают различий, а адаптируемость рассматривают как частный случай управляемости. Разъясним суть понятий управляемости и на­блюдаемости в САУ.

Управляемость САУ - САУ управляема (полностью управ­ляема), если она может быть переведена в произвольный мо­мент времени из любого начального состояния x(t₀) в любое другое путем приложения кусочно-непрерывного воздействия , за конечный интервал времени .

Наблюдаемость САУ (дуальное понятие управляемости) – САУ наблюдаема (полностью наблюдаема), если все ее пере­менные состояния можно непосредственно или косвенно опре­делить по выходному (измеряемому) вектору системы. При на­личии какой-либо переменной состояния, изменение которой не влияет на выходной вектор САУ, система не вполне наблюдае­ма, т.е. имеет место неполная наблюдаемость.

Для оценки управляемости и наблюдаемости линейных ста­ционарных САУ применяют критерии Гильберта и Калмана. Пер­вый из них основан на использовании канонического уравнения состояния. Второй использует матрицы управляемости размерности п(пт) или матри­цы наблюдаемости размерности . Например, если матрицы М и L имеют ранг п, то САУ полностью управляема и наблюдаема.

Принцип дуальности (двойственности) дает возможность оценивать по условиям наблюдаемости одной САУ управляе­мость другой (сопряженной) или по условиям управляемости – наблюдаемость другой сопряженной системы.

17.

20. Передаточные функции стационарных линейных систем, описываемых обыкновенными дифференциальными уравне­ниями, являются отношениями полиномов с действительными коэффициентами. Такие полиномы имеют только действитель­ные и комплексные попарно сопряженные корни. При разложе­нии этих полиномов на множители каждый действительный ко­рень даст линейный относительно р двучлен, а каждая пара комплексно сопряженных корней – квадратный трехчлен относи­тельно р с действительными коэффициентами. Каждый нуле­вой корень даст дополнительный множитель р. Поэтому отно­шение полиномов (2.11.1) можно переписать в следующем виде: 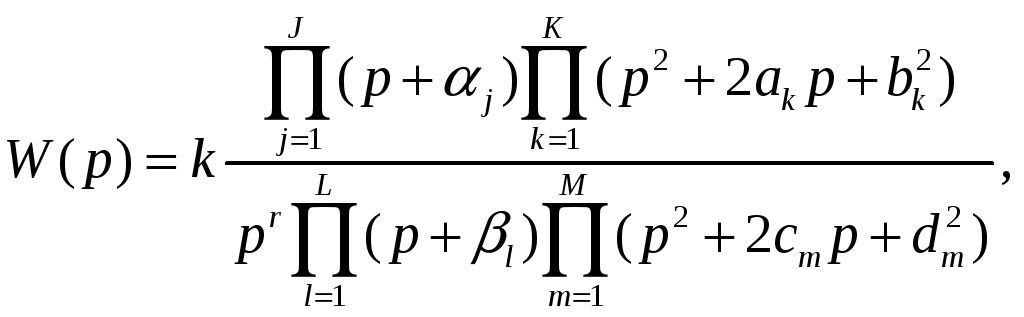(2.12.1) где – любое целое число.

Для исследования стационарных линейных систем удобно ввести элементарные типовые стационарные линейные звенья, передаточными функциями которых являются отдельные про­стейшие множители в формуле (2.12.1):

идеальный дифференциатор ;

форсирующее звено 1-го порядка ;

форсирующее звено 2-го порядка ;

идеальный интегратор W_u(p) = k/p;

статическое звено 1-го порядка ;

- статическое звено 2-го порядка .

Перечисленных шести элементарных типовых звеньев вполне достаточно для исследования систем, описываемых уравнениями вида (2.9.1), (2.9.8). Иногда целесообразно рассмат­ривать как отдельное элементарное звено идеальный безынерционный усилитель – .

21. 4.1. Передаточная функция и характеристики разомкнутой цепи звеньев

Системы автоматического управления (САУ) как правило, являются замкнутыми системами, но при проектировании и анализе качества процесса управления часто возникает необходимость рассмотрения разомкнутой цепи звеньев, которая затем замыкается. Предварительно рассмотрим различные способы соединения динамических звеньев между собой.

4.1.1. Цепь из последовательно соединенных звеньев

Структурная схема последовательного соединения представлена на рис.4.1.

Рис.4.1. Структурная схема последовательного соединения звеньев

Предположим, что все передаточные функции, входящие в рассматриваемое соединение, известны

Если перемножить между собой все левые части передаточных функций и все правые части, то получится передаточная функция последовательной цепи звеньев

(4.1)

Передаточная функция разомкнутой цепи последовательно соединенных звеньев равна произведению передаточных функций всех звеньев.

4.1.2. Цепь из параллельно соединенных звеньев

Структурная схема параллельного соединения представлена на рис.4.2. Если известны все передаточные функции звеньев , то выходной сигнал

Рис.4.2. Структурная схема параллельного соединения звеньев

цепи , следовательно, передаточная функция параллельно соединенных звеньев имеет вид

(4.2)

Передаточная функция разомкнутой цепи параллельно соединенных звеньев равна сумме передаточных функций всех звеньев.

4.1.3. Цепи с местной обратной связью

Структурная схема цепи с местной обратной связью (ОС) приведена на рис.4.3.

Рис.4.3. Структурная схема цепи с местной ОС

На рис.4.3. знаками «» обозначается знак сигнала, поступающего из цепи обратной связи. При отрицательной ОС (ООС) , а при положительной ОС (ПОС) . Составим систему уравнений, описывающую динамическое поведение звена с ОС

(4.3)

Следовательно, передаточная функция цепи с ОС будет иметь вид

(4.4)

Передаточная функция цепи с местной ОС равна отношению передаточной функции прямой цепи к выражению , причем, знак «+» соответствует цепи с ООС, а знак «–» сответствует ПОС.

Если обратная связь представляет собой пропорциональное звено, то такая ОС называется жесткой обратной связью (ЖОС).

Если обратная связь содержит звенья дифференцирующего типа с передаточными функциями или и т.п., то такая обратная связь называется гибкой ОС (ГОС) или дифференцирующей ОС.

Если обратная связь содержит звенья интегрирующего типа с передаточными функциями вида , то такая обратная связь называется интегрирующей ОС.

22. Линейные законы регулирования. Понятие о законах регулирования

Понятие о законах регулирования

Под законом регулирования, или, в более общем случае, законом управления понимается математическая форма преоб­разований задающих воздействий, возмущений, воздействий обратных связей, определяющих управляющие воздействия u(t). Иными словами, это функциональная зависимость, в соот­ветствии с которой УУ формирует управляющие воздействия u(t) . Она может быть представлена в следующем виде: u(t)=F(x,g,f), где F – некоторая, в общем случае нелинейная, функция от ошибки х, задающего g и возмущающего воздействия f, а также их производных и интегралов по времени.

Линейные законы регулирования

Мы рассмотрим только линейные законы, когда УУ (регуля­тор) вырабатывает величину u(t) в функции ошибки в соответ­ствии с линейной формой: При рассмотрении линейных законов дополни­тельно предположим, что ОУ (ОР) представляет собой звено статического типа. Это означает, что в установившемся состоя­нии между регулируемой величиной и управляющим воздейст­вием существует пропорциональная зависимость, вытекающая из при равенстве нулю возмущающих воздействий: