Приближение функции с использованием метода наименьших квадратов Определение коэффициентов линейной регрессии с помощью решающего блока

a := 1 b := 1 - Задание начальных значений переменных

Given - Ключевое слово, указывающее на начало блока

- Совокупность решаемых уравнений

- Функция Find находит искомые значения

коэффициентов в уравнениях.

После нахождения коэффициентов линейного уравнения записывается уравнение связи и строится график корреляционной зависимости

- Уравнение связи

Вопрос 13. Численное дифференцирование. Основные понятия, геометрическая интерпретация. Вторая производная. Метод Эйлера

Численное дифференцирование – функция трудно (невозможно) продифференцировать аналитически (Ex – функция задана таблицей).

Вычисление 1^ой производной

Пусть f(x) дифференцируема в окрестности точки x. Из определения производной следует

и (1.1)

Здесь h>0 - шаг.

Для оценки погрешностей

Г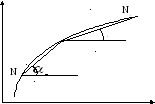еометрия интерпретируется f’(x)=tg,

= tg₊;=tg_-

Вычисление 2^ой производной

Выражение для погрешности

Вопрос 14. Численное дифференцирование. Задача Коши. Численное дифференцирование с использованием формулы Тейлора

Решением обыкновенного ДУ первого порядка y’(t)=f(t,y(t)) (*) называется дифференциальная функция y(t), которая, при подстановке в (*), обращает его в тождество.

Чтобы выделить из семейства решений ДУ(*) одно конкретное, задают начальные условие y(t₀)=y₀ (**). Задачу нахождения при t>t₀ решения y(t) ДУ (*), удовлетворяющего (**), называют задачей Коши.

Простейшие дискретный аналог ДУ (*)

Отсюда следует расчетная формула численного дифференцирования по методу Эйлера.

4. Использование формулы Тейлора

Разложение в ряд Тейлора

y’(t) – известна = f(t,y(t))

y”(t) = f’_t + f’_yy’ – дифференцирование сложной функции

y”’(t) = f⁽²⁾_tt + f⁽²⁾_tyy’ + (f⁽²⁾_yt + f⁽²⁾_yyy’)f + f’_y(f’_t + f’_yy’)

По мере роста порядка (р) усложняются выражения для производных. Недостаток метода Эйлера - значит-я погрешность – на практике редко используется. Желательно поправить расчетную формулу.

Пусть y(t) – решение ДУ y’(t)=f(t,y(t)), удовлетворяет условию y(t_n)=y_n

Пусть (1.3)

- угловой коэффициент секущей, проходящей через точки (t_n, y(t_n)) и (t_n+1, y(t_n+1)) графика функции y(t). Ясно, что «метод» y_n+1 = y_n + hK_n имеет нулевую локальную погрешность. Следовательно нужно научиться вычислять значение K_n. Интегрируя и используя формулу Ньютона – Лейбница приходим к равенству

(1.4)

Из (1.3) и (1.4) следует K_n =

Примечание. Для приближенного вычисления интеграла используется формула прямоугольников:

приводит к методу Эйлера.

Но больший порядок точности имеет формула трапеций:

Итого приходим к правилу трапеций:

Если подставим в правую часть значение y_n+1 «предсказанное» методом Эйлера, получим в результате метод Эйлера-Коши:

Этот метод относится к методам прогноза и коррекции.