30. Які ви знаете властивості опорних планів транспортної задачі?

Опорним планом транспортної задачі є такий допустимий її план, що містить не більш ніж m + n – 1 додатних компонент, а всі інші його компоненти дорівнюють нулю. Такий план є невиродженим. Якщо ж кількість базисних змінних менша ніж m + n – 1, то маємо вироджений опорний план.

Якщо умови транспортної задачі і її опорний план записані у вигляді транспортної таблиці,то клітини, в яких (ненульові значення поставок), називаються заповненими, всі інші — пустими. Заповнені клітини відповідають базисним змінним і для невиродженого плану їх кількість дорівнює m + n – 1.

Циклом називають таку послідовність заповнених клітин таблиці, яка задовольняє умову, що лише дві сусідні клітини містяться або в одному рядку, або в одному стовпці таблиці, причому перша клітина циклу є і його останньою клітиною. Якщо для певного набору заповнених клітин неможливо побудувати цикл, то така послідовність клітин є ациклічною.

1)Кількість клітин, які утворюють будь-який цикл транспортної задачі, завжди парна.

2)Щоб деякий план транспортної задачі був опор­ним, необхідно і достатньо його ациклічності.

3)Будь-яка сукупність з клітин матриці транспортної задачі утворює цикл.

4)Якщо всі запаси і всі потреби 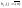є невід’ємними цілими числами, то будь-який опорний план складається із значень, що є цілими числами.

31. Побудуйте просту економіко-математичну модель. Запишіть до неї двоїсту. Дайте економічну інтерпретацію двоїстих оцінок.

max F = –5x₁ + 2x₂;

Розв’язання. Перш ніж записати двоїсту задачу, необхідно пряму задачу звести до стандартного вигляду. Оскільки цільова функція F максимізується і в системі обмежень є нерівності, то вони мусять мати знак «». Тому перше обмеження задачі помножимо на (–1). Після цього знак нерівності зміниться на протилежний. Отримаємо:

max F = –5x₁ + 2x₂;

Тепер за відповідними правилами складемо двоїсту задачу:

;

Економічна інтерпретація двоїстих оцінок.

Якщо для виготовлення всієї продукції в обсязі, що визначається оптимальним планом Х^*, витрати одного і-го ресурсу строго менші, ніж його загальний обсяг , то відповідна оцінка такого ресурсу (компонента оптимального плану двоїстої задачі) буде дорівнювати нулю, тобто такий ресурс за даних умов для виробництва не є «цінним». Якщо ж витрати ресурсу дорівнюють його наявному обсягові , тобто його використано повністю, то він є «цінним» для виробництва, і його оцінка буде строго більшою від нуля.

У разі, коли деяке j-те обмеження виконується як нерівність, тобто всі витрати на виробництво одиниці j-го виду продукції перевищують її ціну сj, виробництво такого виду продукції є недоцільним, і в оптимальному плані прямої задачі обсяг такої продукції дорівнює нулю. Якщо витрати на виробництво j-го виду продукції дорівнюють ціні одиниці продукції , то її необхідно виготовляти в обсязі, який визначає оптимальний план прямої задачі .

Двоїсті оцінки є унікальним інструментом, який дає змогу зіставляти непорівнянні речі. Очевидно, що неможливим є просте зіставлення величин, які мають різні одиниці вимірювання. Якщо взяти як приклад виробничу задачу, то цікавим є питання: як змінюватиметься значення цільової функції (може вимірюватися в грошових одиницях) за зміни обсягів різних ресурсів (можуть вимірюватися в тоннах, м2, люд./год, га тощо).