
- •Элементарные функции Степень и степенная функция с натуральным показателем
- •40. , Если
- •Степень и степенная функция с целым отрицательным показателем
- •20. , Если
- •40. , Если
- •2. Если – чётное, то функция – чётная. Если – нечётное, то функция – нечётная.
- •Показательная функция с рациональным показателем
- •Понятие степени с иррациональным показателем.
- •Показательная функция с действительным показателем
- •Логарифмическая функция
- •Тригонометрические функции: синус, косинус.
Показательная функция с действительным показателем
Определение.
Показательной функцией с действительным
показателем называется функция вида
![]() ,
,
![]() ,
,
![]() .
.
Свойства.
-
После того как было введено понятие степени положительного числа с любым рациональным и иррациональным показателем можно сказать, что показательная функция определена на множестве действительных чисел.
-
Функция
 принимает лишь положительные значения.
принимает лишь положительные значения.
-
Если
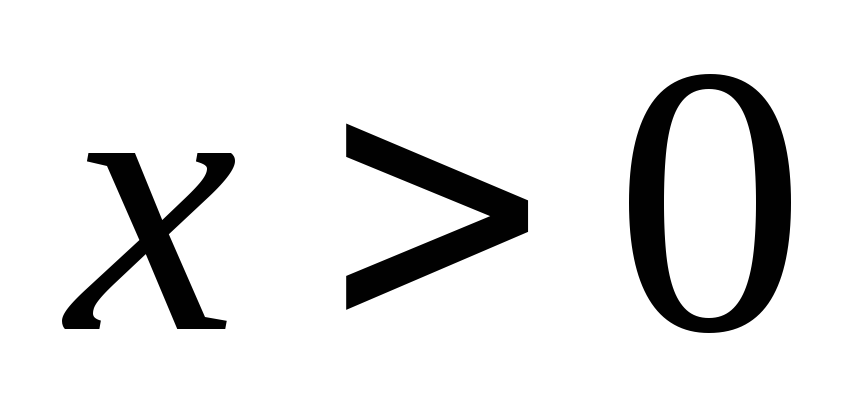 ,
то
,
то
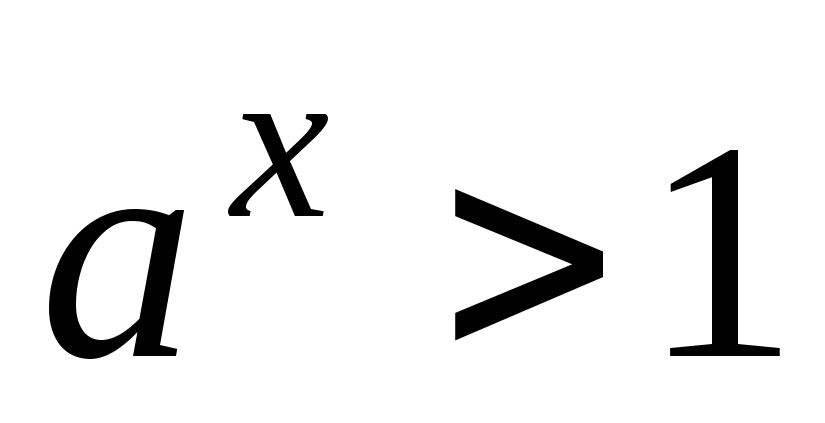 при
при
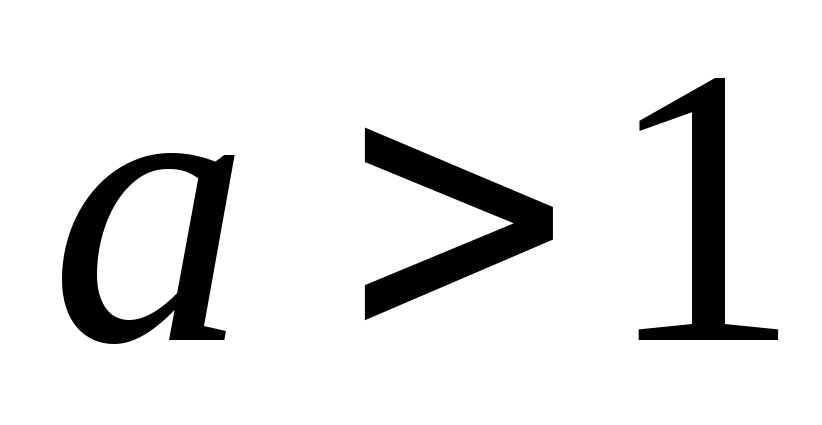 ,
и
,
и
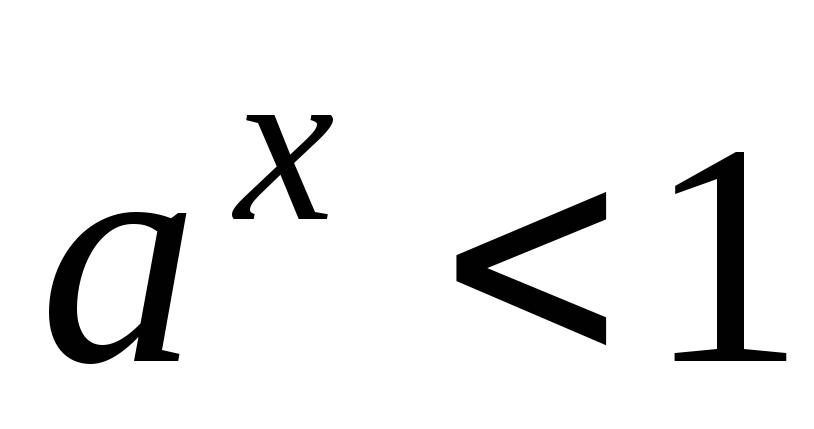 при
при
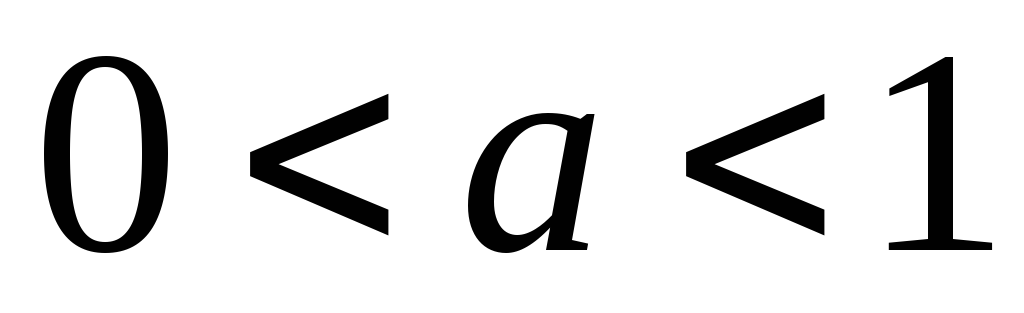 .
.
Если
![]() ,
то
,
то
![]() при
при
![]() ,
и
,
и
![]() при
при
![]() .
.
-
Характеристическое свойство:
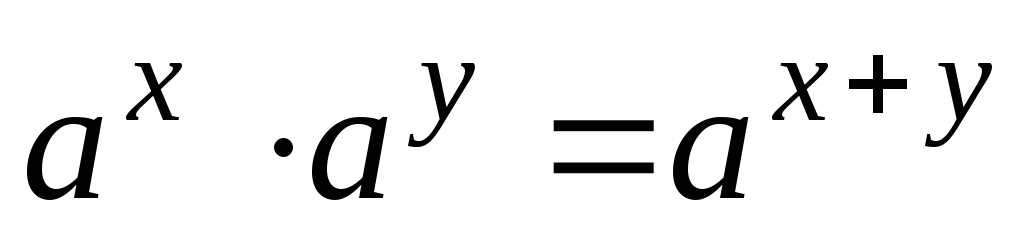
Следствие 1.
![]()
Следствие 2.
![]()
-
Функция
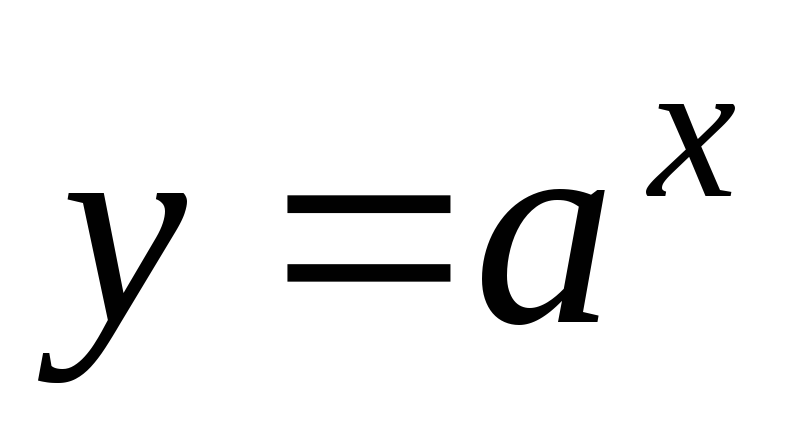 строго возрастает на множестве
действительных чисел при
строго возрастает на множестве
действительных чисел при
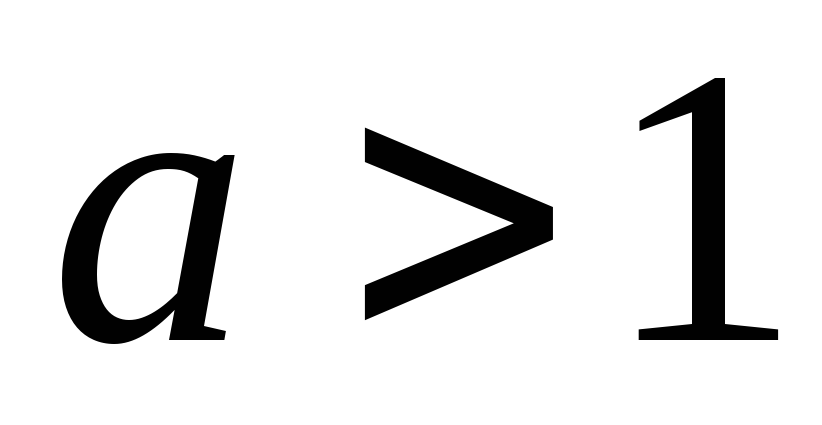 и строго убывает на этом множестве при
и строго убывает на этом множестве при
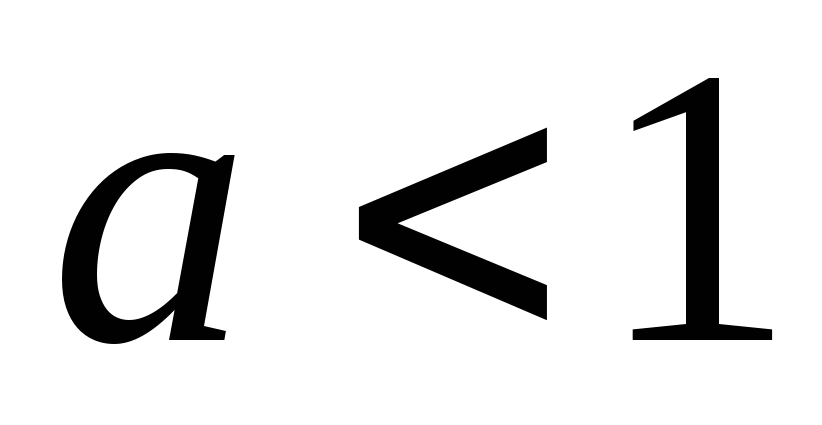 .
.
-
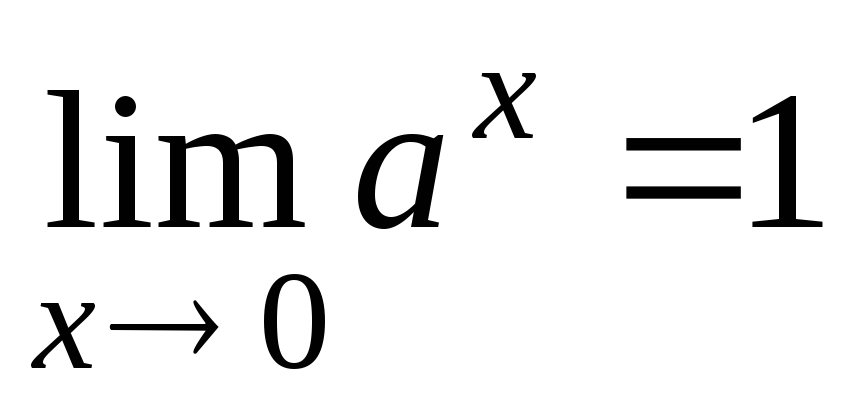
-
Функция
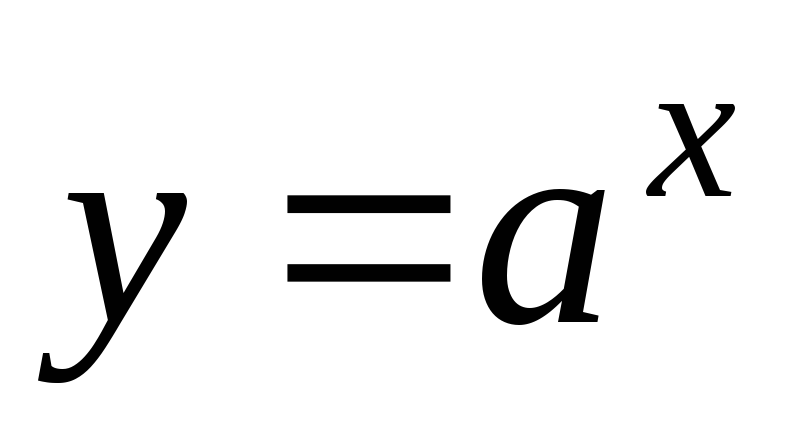 непрерывна на множестве действительных
чисел.
непрерывна на множестве действительных
чисел.
-
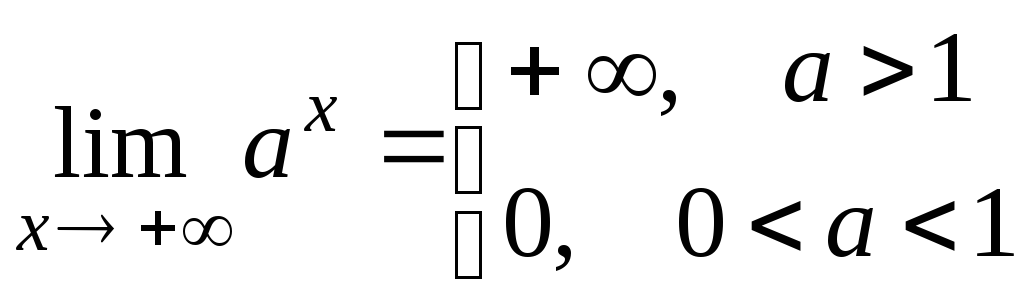 и
и
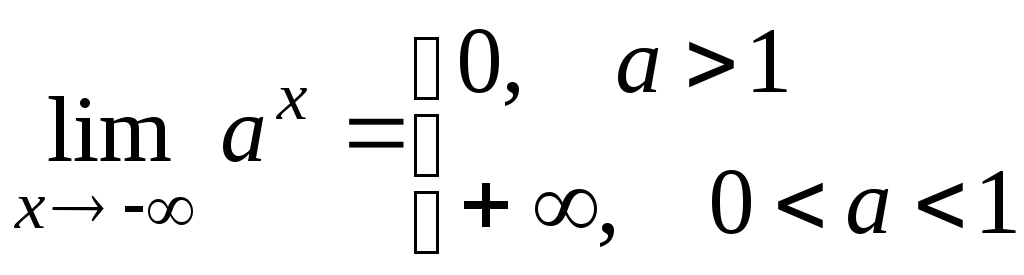
-
Множеством значений функции
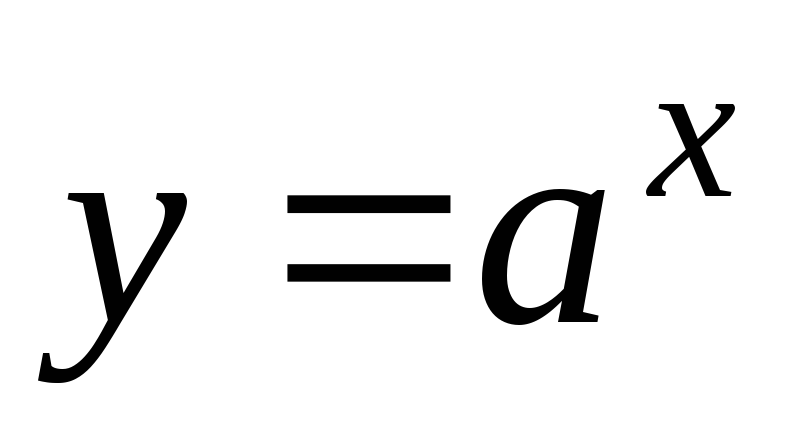 является интервал
является интервал
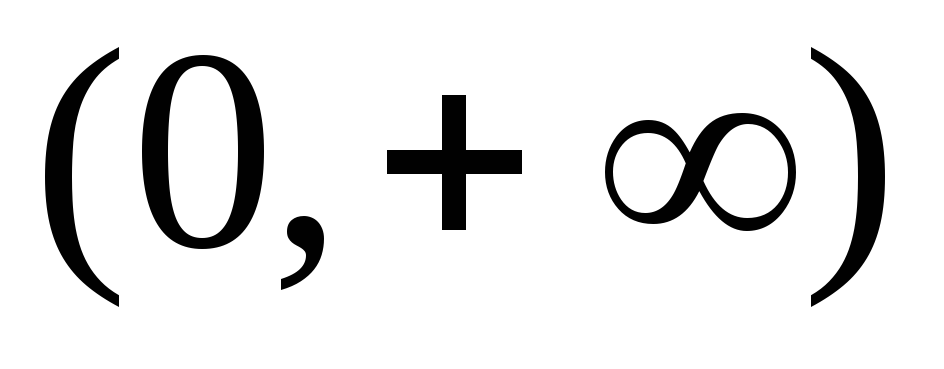 .
.

Логарифмическая функция
Функция вводится как обратная функция к показательной функции.
Пусть
![]() .
Рассмотрим функцию
.
Рассмотрим функцию
![]() .
Она непрерывна и строго возрастает на
множестве
.
Она непрерывна и строго возрастает на
множестве
![]() ,
причём существует
,
причём существует
![]() и
и
![]() .
Тогда по теореме о существовании обратной
функции в случае интервала получаем,
что на интервале
.
Тогда по теореме о существовании обратной
функции в случае интервала получаем,
что на интервале
![]() существует функция, обратная данной,
непрерывная и строго возрастающая на
интервале
существует функция, обратная данной,
непрерывная и строго возрастающая на
интервале
![]() .
Будем обозначать её
.
Будем обозначать её
![]() и называть – логарифмической
функцией по основанию
и называть – логарифмической
функцией по основанию
![]() .
Переходя к принятому обозначению
аргумента через
.
Переходя к принятому обозначению
аргумента через
![]() ,
запишем функцию в виде
,
запишем функцию в виде
![]() .
.
Свойства.
-
Функция
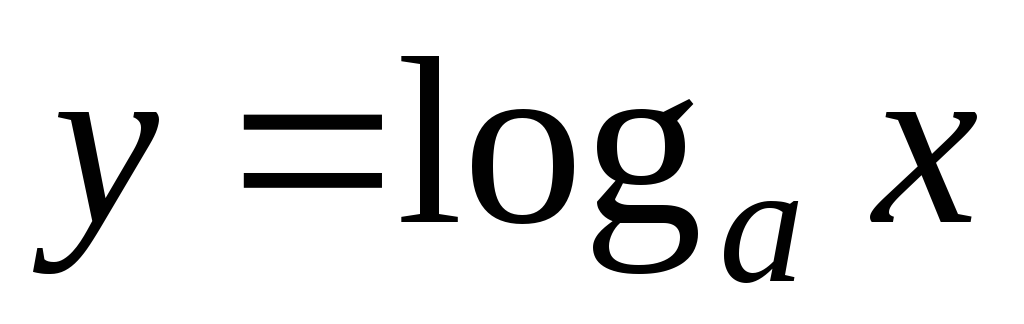 определена
на интервале
определена
на интервале
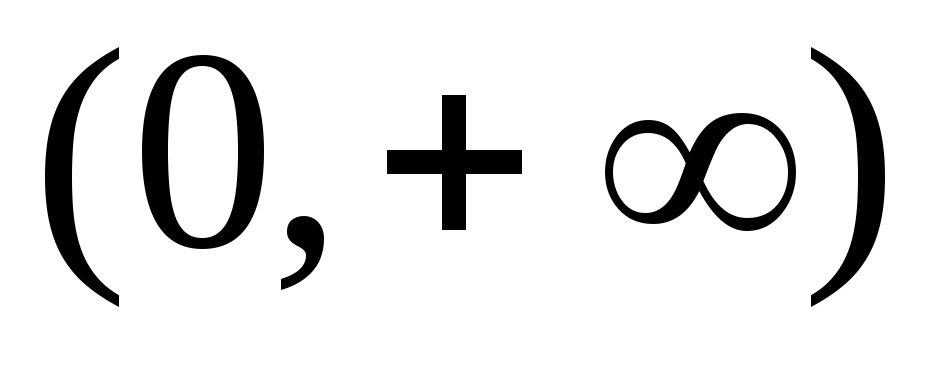 .
. -
Функция строго возрастает на
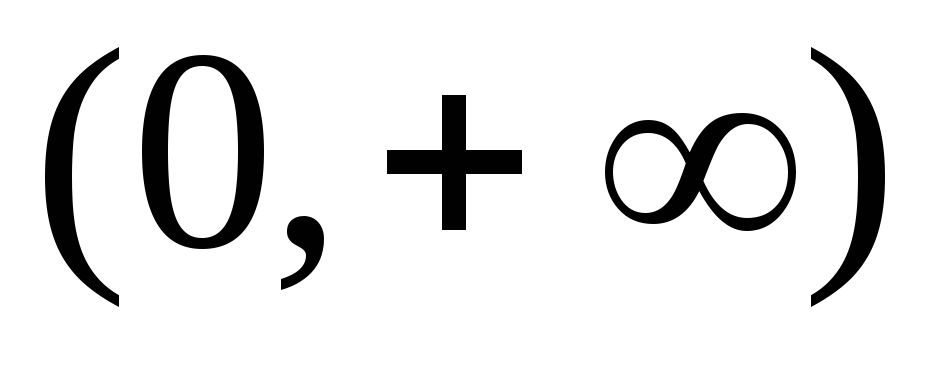 .
. -
Функция непрерывна на
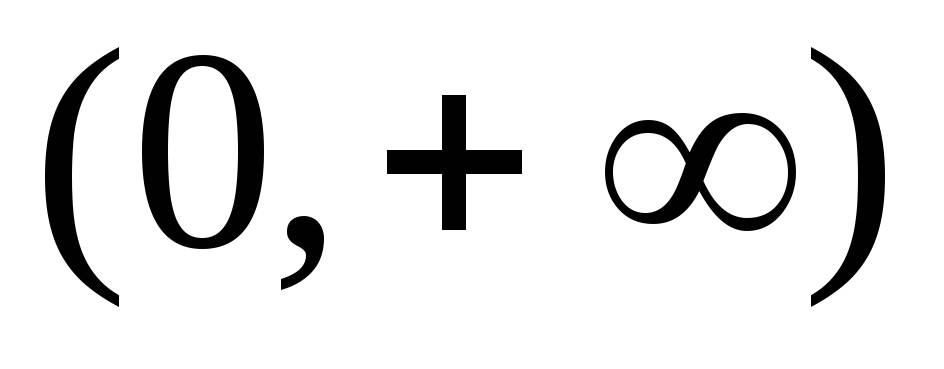 .
. -
Множеством значений является интервал
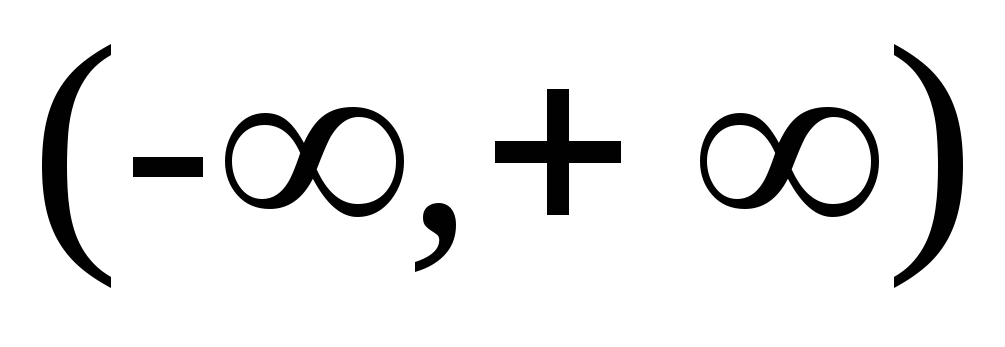 .
. -
Из того что
 ,
а
,
а
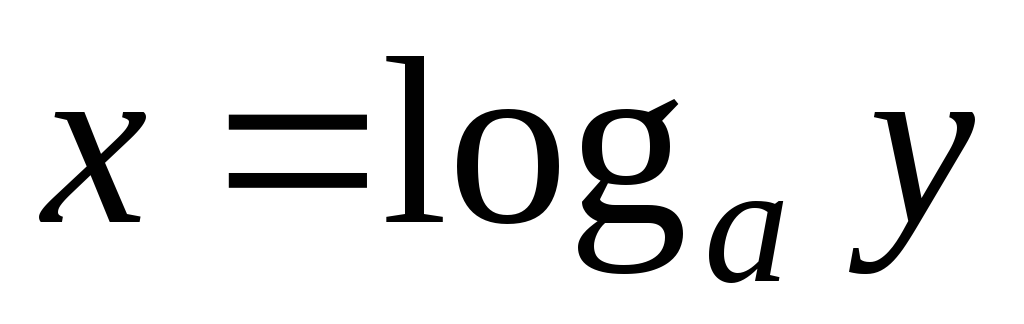 получаем тождества
получаем тождества
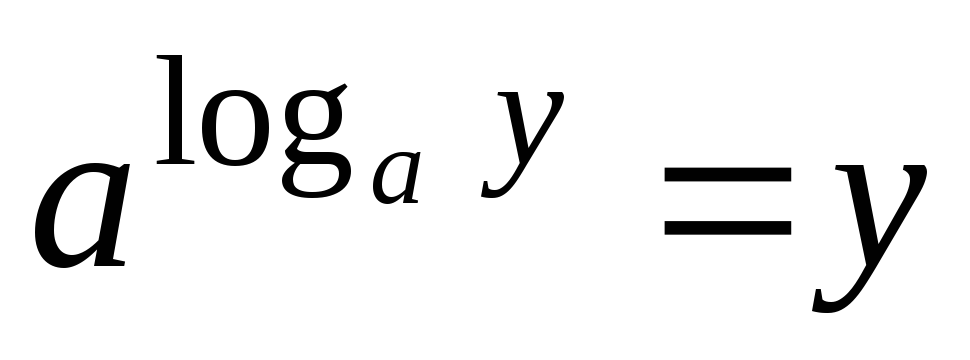 и
и
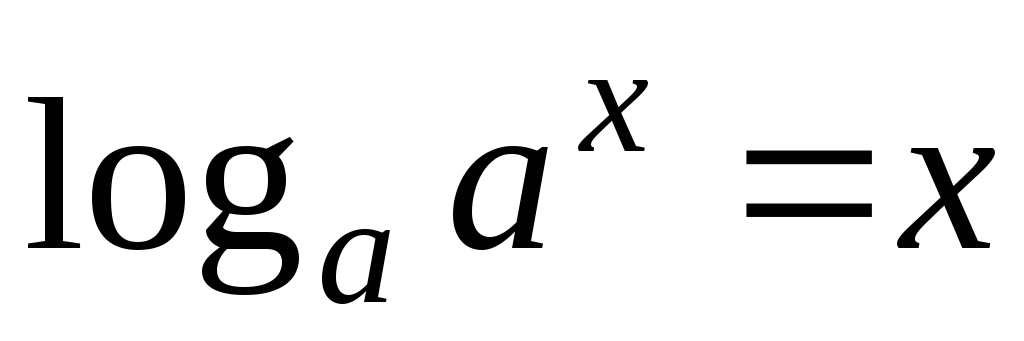 .
. -
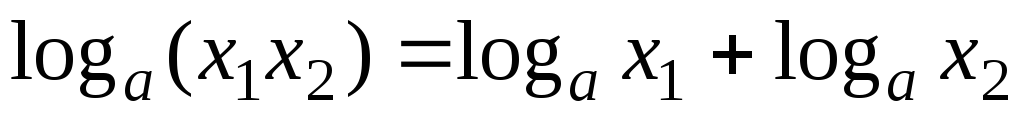 ,
где
,
где
 .
. -
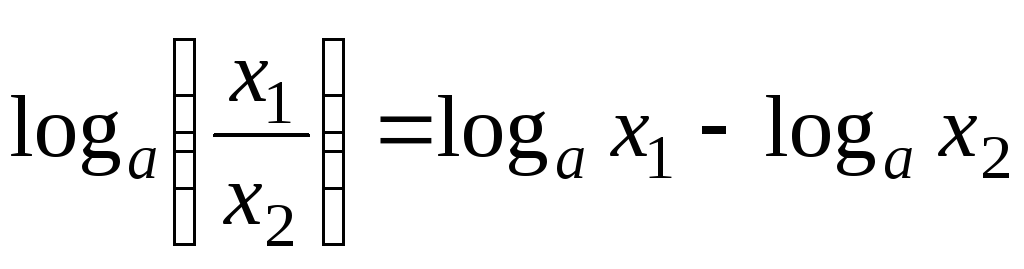
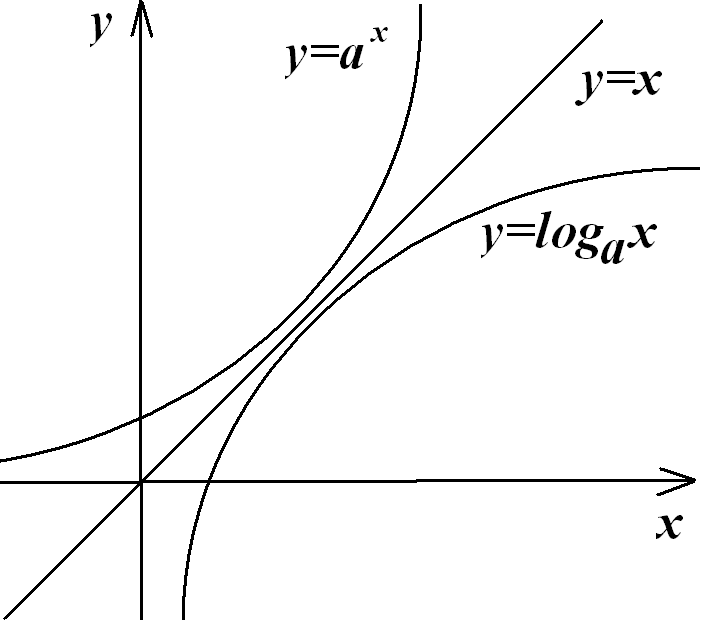 ,
где
,
где
 .
. -
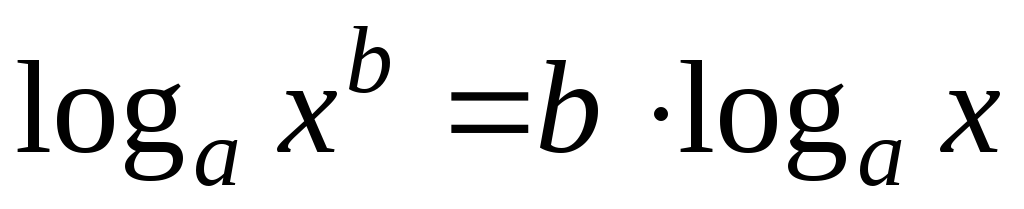 ,
где
,
где
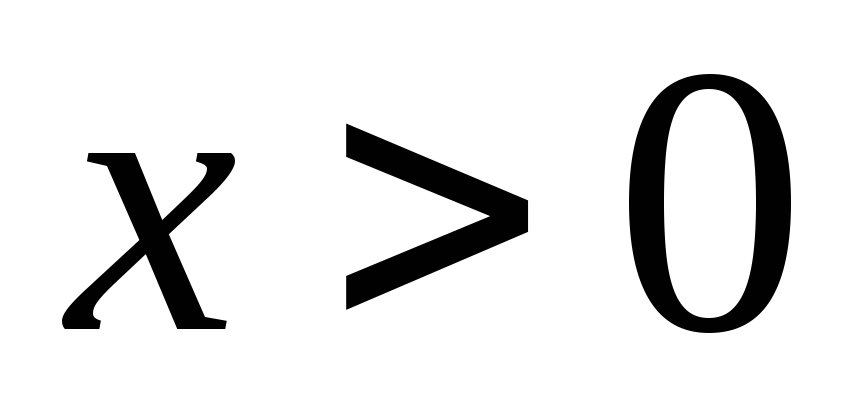 .
. -
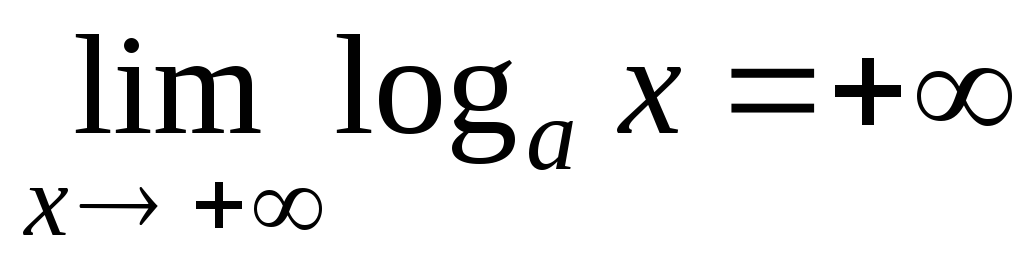
-

А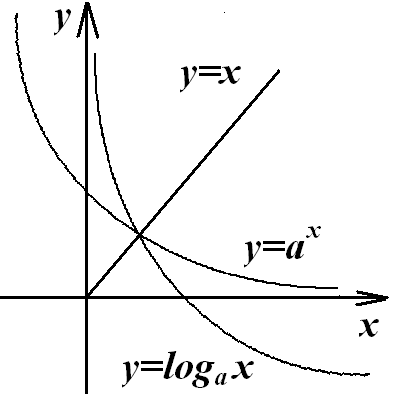 налогично
вводится логарифмическая функция по
основанию
налогично
вводится логарифмическая функция по
основанию
![]() при
при
![]() ,
которая по теореме о существовании
обратной функции обладает свойствами:
,
которая по теореме о существовании
обратной функции обладает свойствами:
-
Функция
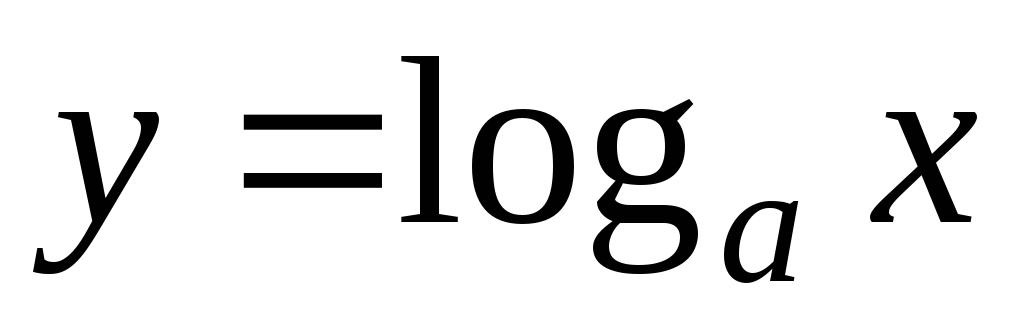 определена
на интервале
определена
на интервале
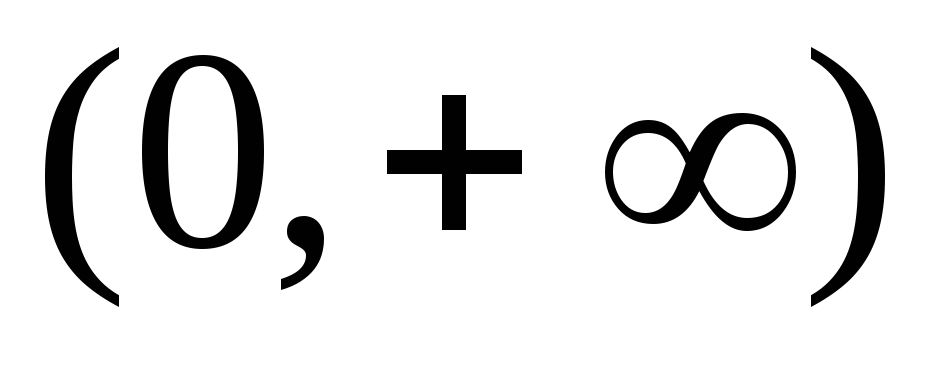 .
. -
Функция строго возрастает на
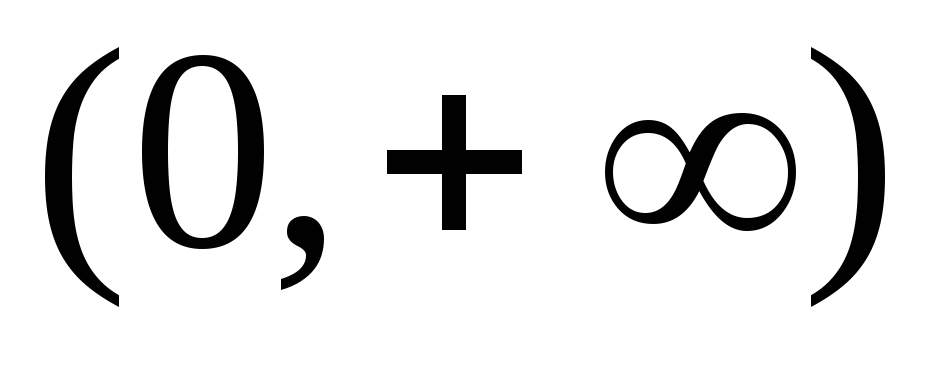 .
. -
Функция непрерывна на
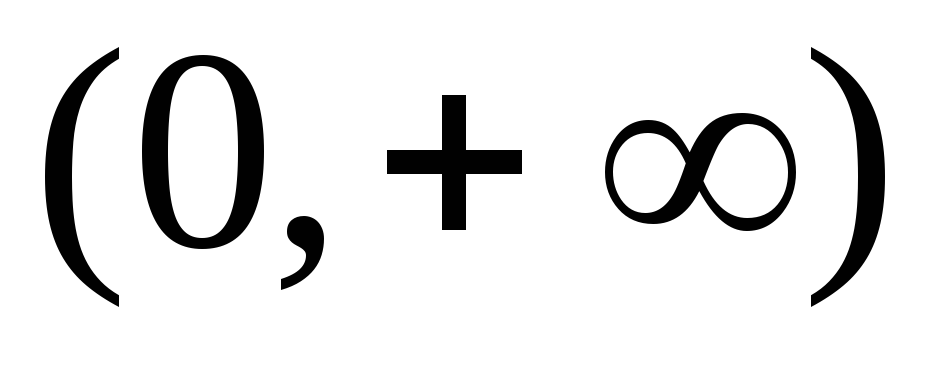 .
. -
Множеством значений является интервал
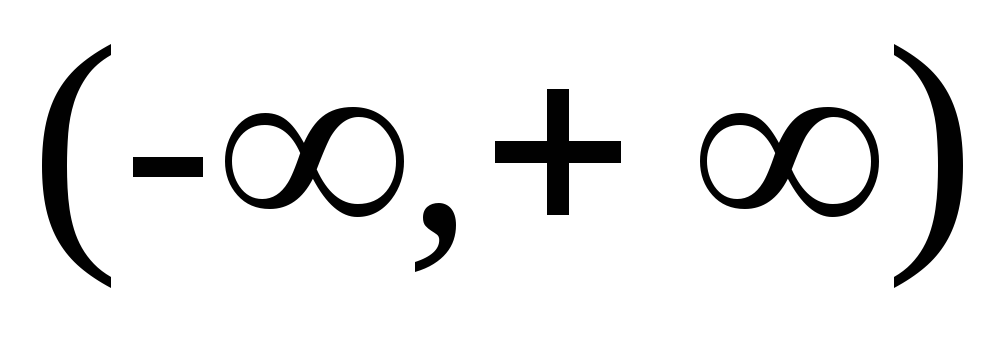 .
. -

-
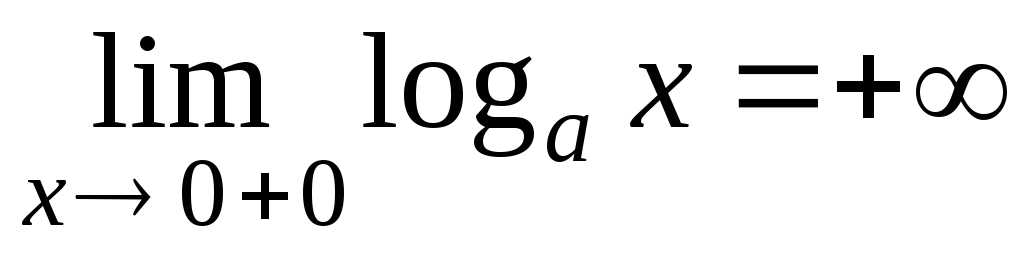
Тригонометрические функции: синус, косинус.
Р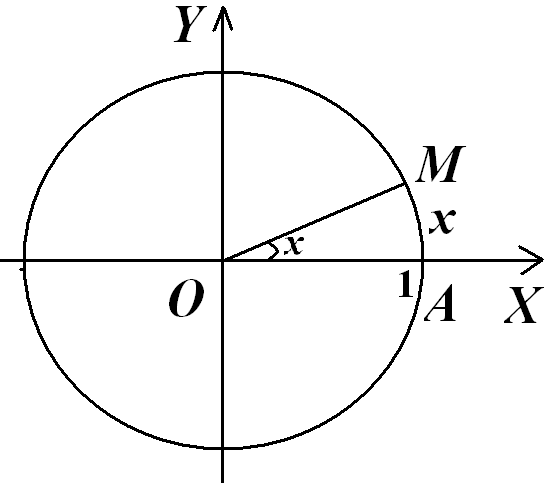 ассмотрим
на плоскости
ассмотрим
на плоскости
![]() единичный круг. Примем точку
единичный круг. Примем точку
![]() за начальную точку на окружности. Пусть
точка
за начальную точку на окружности. Пусть
точка
![]() – произвольная точка окружности и может
двигаться по окружности по и против
часовой стрелки. Движение точки
– произвольная точка окружности и может
двигаться по окружности по и против
часовой стрелки. Движение точки
![]() против часовой стрелки считается
положительным направлением. Движение
не ограничивается одним оборотом.
против часовой стрелки считается
положительным направлением. Движение
не ограничивается одним оборотом.
Пусть точка
![]() движется в положительном направлении.
Положение точки
движется в положительном направлении.
Положение точки
![]() на окружности можно определить длиной
на окружности можно определить длиной
![]() дуги
дуги
![]() .
Так как
.
Так как
![]() ,
то длина
,
то длина
![]() численно совпадает с радианной мерой
угла между вектором
численно совпадает с радианной мерой
угла между вектором
![]() и положительным направлением оси
и положительным направлением оси
![]() .
.
Определение.
Абсцисса
![]() и ордината
и ордината
![]() точки
точки
![]() являются функциями величины
являются функциями величины
![]() и называются косинусом
и синусом
аргумента
и называются косинусом
и синусом
аргумента
![]() ,
при этом
,
при этом
![]() ,
,
![]() .
.
Так как
![]() –
координаты точки единичной окружности,
то
–
координаты точки единичной окружности,
то
![]() ,
,
![]() .
.
Свойства функций.
-

-
Функции – периодические с периодом
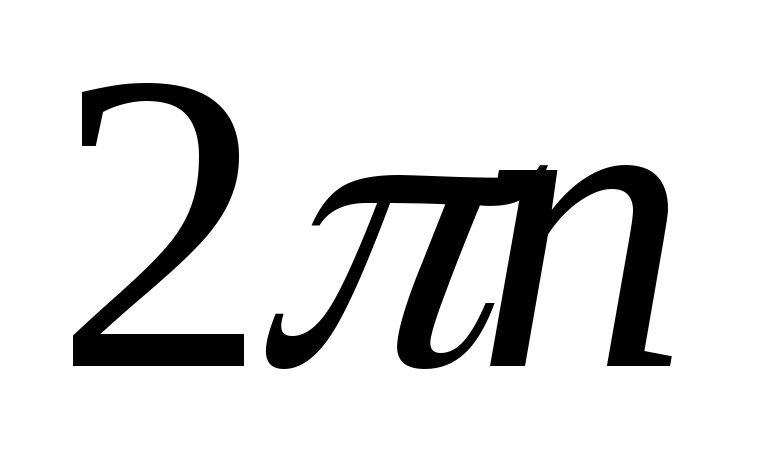 ,
,
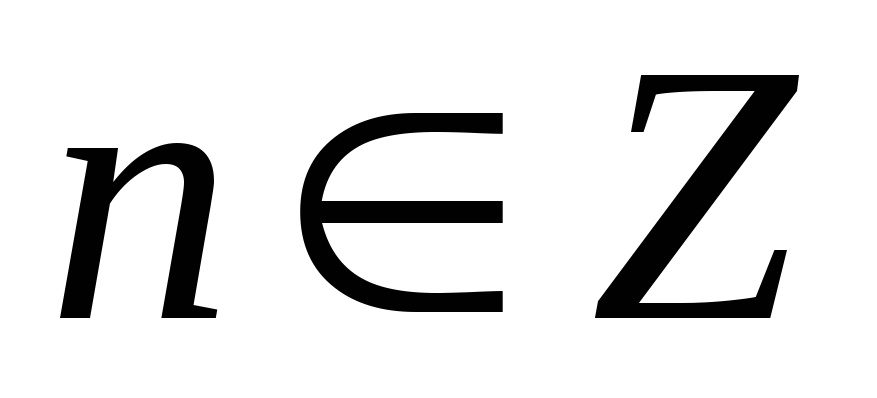 ,
и наименьшим положительным периодом
,
и наименьшим положительным периодом
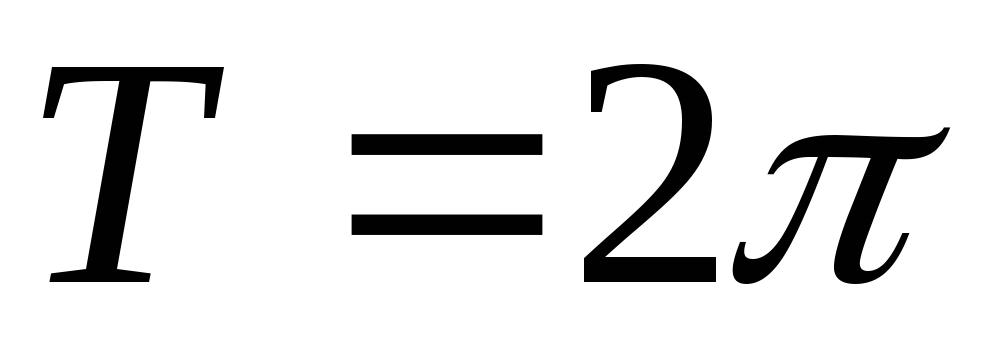
![]()
-
Функции
 ,
,
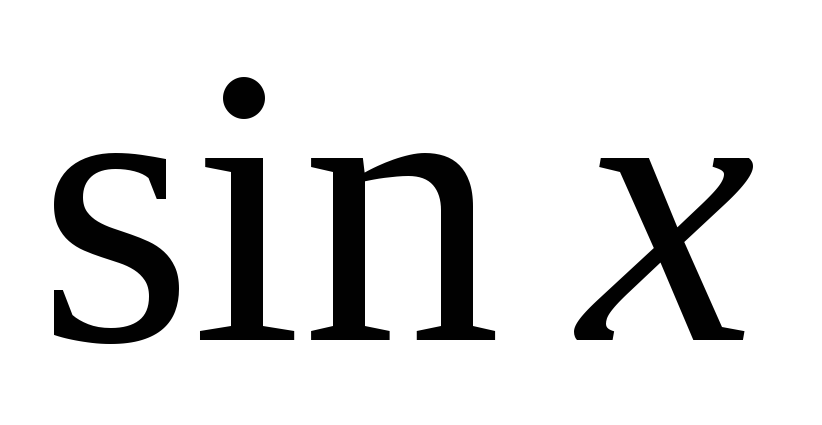 непрерывны в интервале
непрерывны в интервале
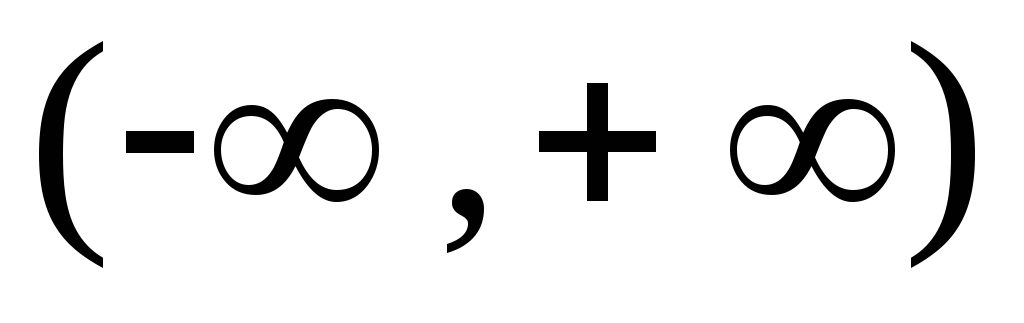 .
.
Доказательство.
Возьмём
любое
![]() и покажем, что функция
и покажем, что функция
![]() непрерывна в
непрерывна в
![]() ,
то есть
,
то есть
![]() ,
то есть для любого
,
то есть для любого
![]() существует
существует
![]() ,
такое что для любых
,
такое что для любых
![]() ,
таких что
,
таких что
![]() выполняется неравенство
выполняется неравенство
![]() .
(1)
.
(1)
![]()
Таким образом,
![]() (2)
(2)
Положим
![]() (3)
(3)
Выберем
![]() .
Тогда из неравенства (3) в силу транзитивности
неравенств (2) и (3) получаем неравенство
(1). Следовательно,
.
Тогда из неравенства (3) в силу транзитивности
неравенств (2) и (3) получаем неравенство
(1). Следовательно,
![]() .
В силу произвольности выбора точки
.
В силу произвольности выбора точки
![]() получаем, что функция
получаем, что функция
![]() непрерывна в
непрерывна в
![]() .
.
Непрерывность в
![]() функции
функции
![]() доказывается аналогично (доказать
самостоятельно).
Ч.Т.Д.
доказывается аналогично (доказать
самостоятельно).
Ч.Т.Д.
-
Функция
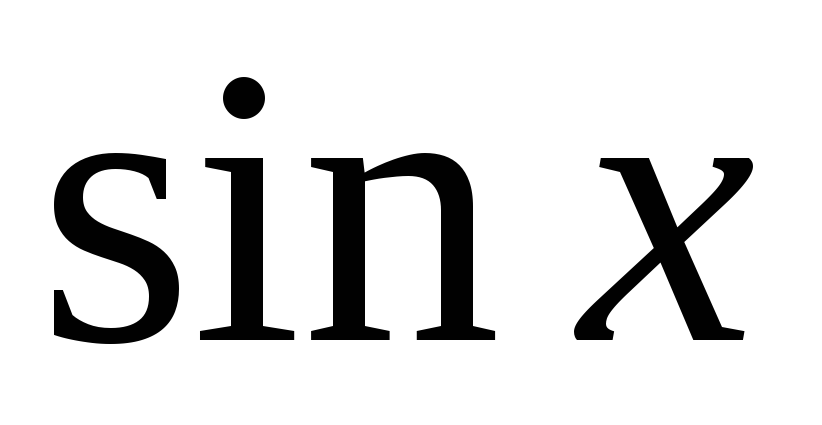 возрастает на
возрастает на
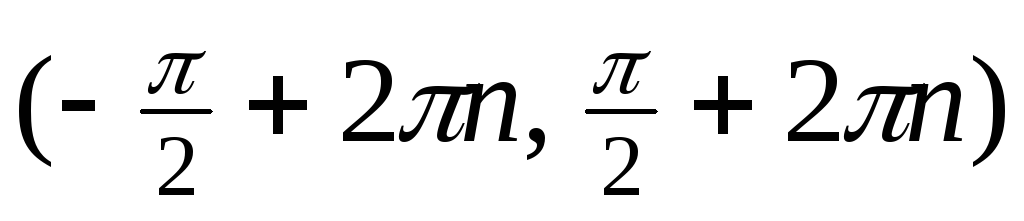 и убывает на
и убывает на
 .
Функция
.
Функция
 возрастает на
возрастает на
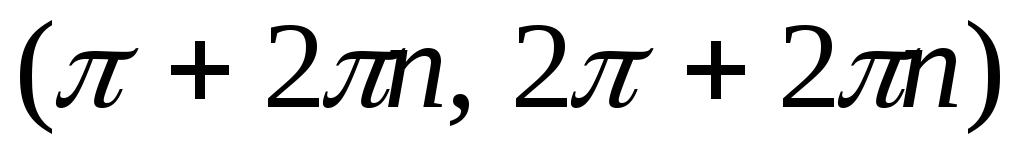 и убывает на
и убывает на
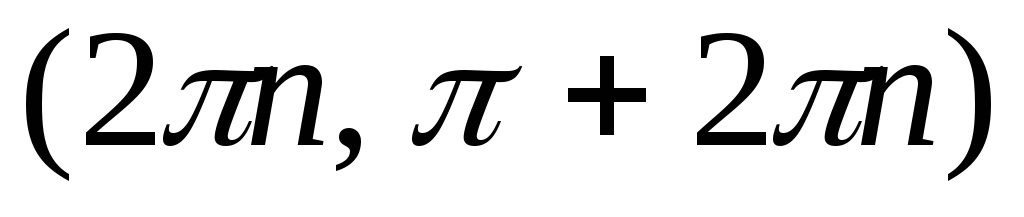 .
.
Доказательство.
Покажем, что функция
![]() возрастает на
возрастает на
![]() .
Пусть
.
Пусть
![]() ,
при этом
,
при этом
![]() .
Найдём
.
Найдём
![]()
![]()
Аналогично:
![]() ,
но так как
,
но так как
![]() ,
то
,
то
![]() .
.
Тогда
![]() ,
,
![]() .
Отсюда
.
Отсюда
![]() и
и
![]() .
.
Аналогично доказываются остальные утверждения. Ч.Т.Д.
-
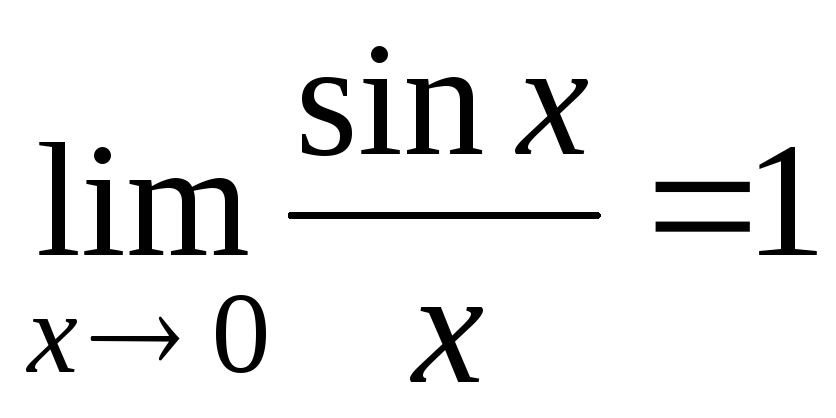
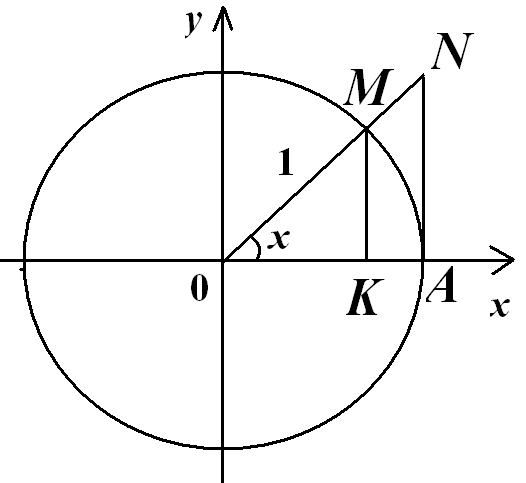 ,
где
,
где
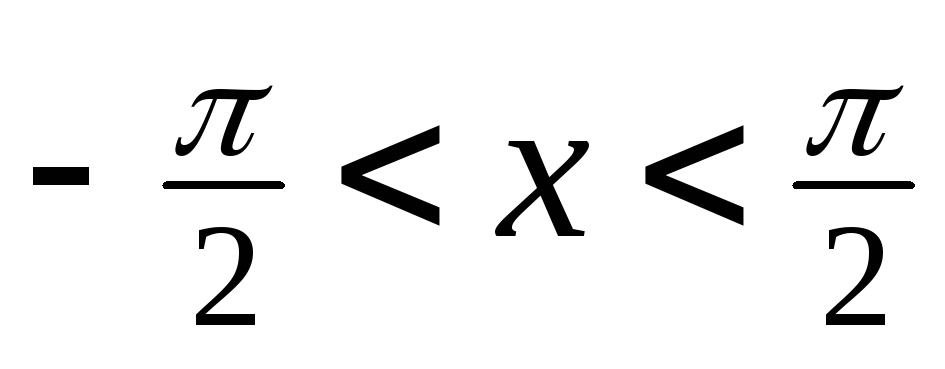
Доказательство.
Пусть
![]() .
Тогда
.
Тогда
![]()
![]()
![]()
Разделим на
![]() :
:
![]() для любого
для любого
![]() .
.
Покажем, что
последнее неравенство выполняется и
для
![]() .
Если
.
Если
![]() ,
то
,
то
![]() .
Тогда
.
Тогда
![]() .
Отсюда
.
Отсюда
![]() .
.
Итак,
![]() для любого
для любого
![]() ,
,
![]() .
Причём
.
Причём
![]() .
Тогда по теореме (если в некоторой
проколотой окрестности точки
.
Тогда по теореме (если в некоторой
проколотой окрестности точки
![]() выполняется неравенство
выполняется неравенство
![]() и
и
![]() ,
то
,
то
![]() )
получаем, что
)
получаем, что
![]() .
Ч.Т.Д.
.
Ч.Т.Д.
-
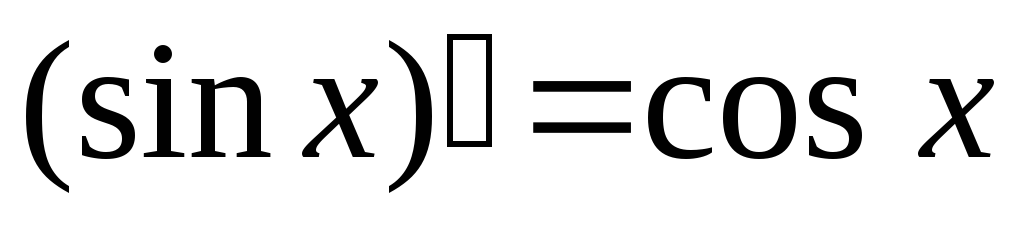 ,
,
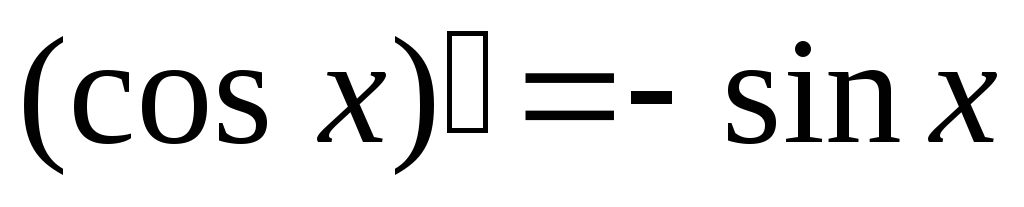
Доказательство.
Докажем
![]() .
Возьмём
произвольную точку
.
Возьмём
произвольную точку
![]() и выберем приращение аргумента
и выберем приращение аргумента
![]() ,
такое что
,
такое что
![]() .
Тогда приращение функции
.
Тогда приращение функции
![]() .
Найдём
.
Найдём
![]() :
:
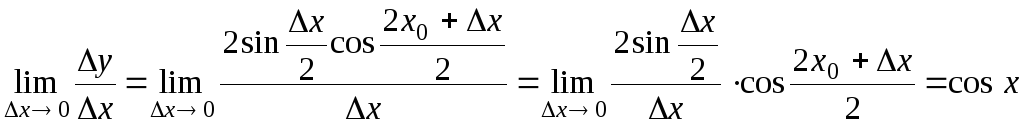
Таким образом,
![]() .
Аналогично доказывается
.
Аналогично доказывается
![]() .
Ч.Т.Д.
.
Ч.Т.Д.
-
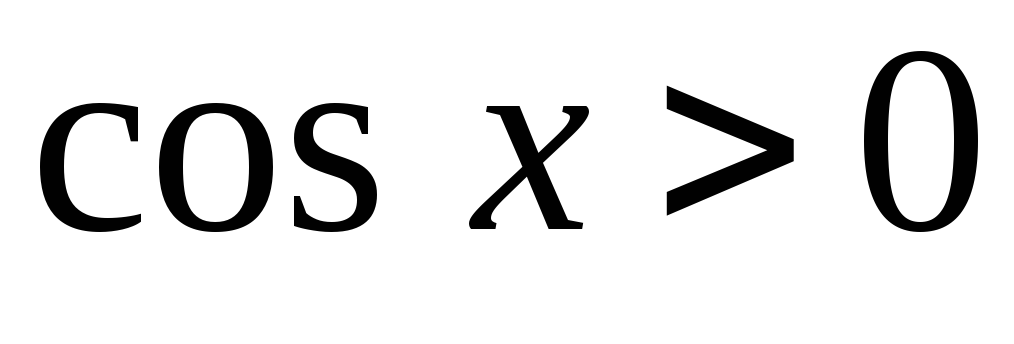 для любого
для любого

![]() для любого
для любого
![]()
![]() для любого
для любого
![]()
![]() для любого
для любого
![]()
-
Множество значений
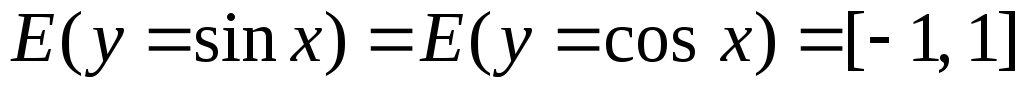
Доказательство.
Известно, что для любого
![]()
![]() .
Возьмём произвольное
.
Возьмём произвольное
![]() и покажем, что существует
и покажем, что существует
![]() ,
такое что
,
такое что
![]() .
.
Функция
![]() непрерывна и строго возрастает на
непрерывна и строго возрастает на
![]() ,
при этом
,
при этом
![]() и
и
![]() .
Тогда по свойству функции, непрерывной
на отрезке получаем, что для любого
.
Тогда по свойству функции, непрерывной
на отрезке получаем, что для любого
![]() существует хотя бы одно
существует хотя бы одно
![]() ,
такое что
,
такое что
![]() .
.
Свойство для
функции
![]() доказывается аналогично. Ч.Т.Д.
доказывается аналогично. Ч.Т.Д.
-
Ф
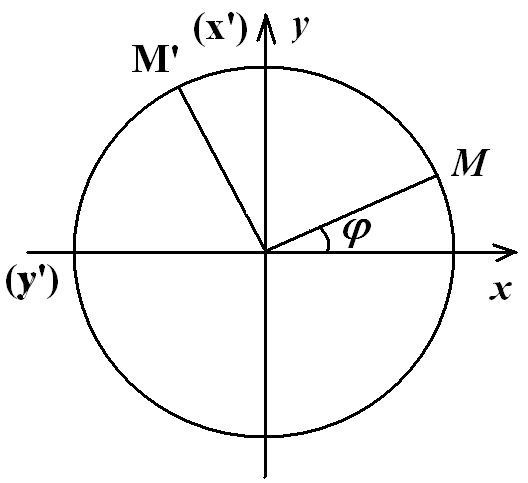 ормулы
приведения для функций с аргументами
ормулы
приведения для функций с аргументами
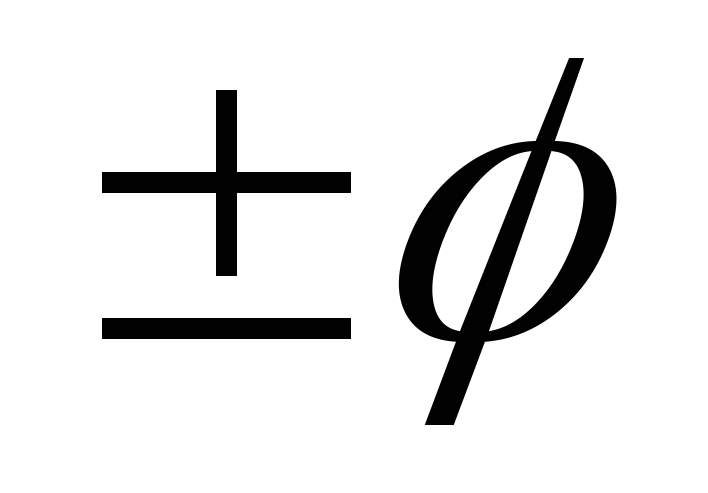 ,
,
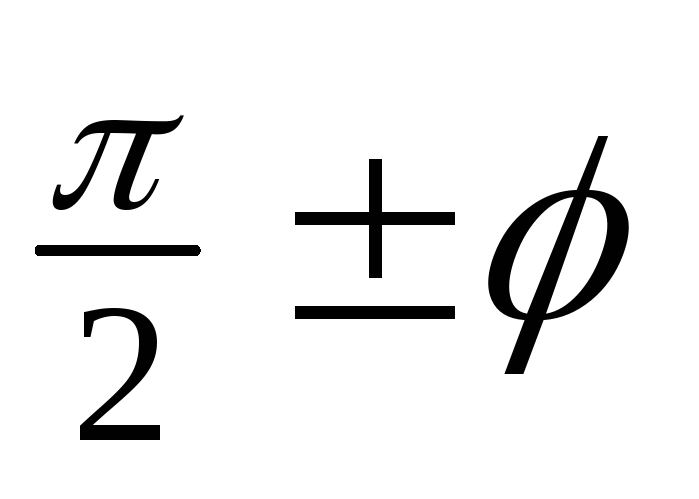 ,
,
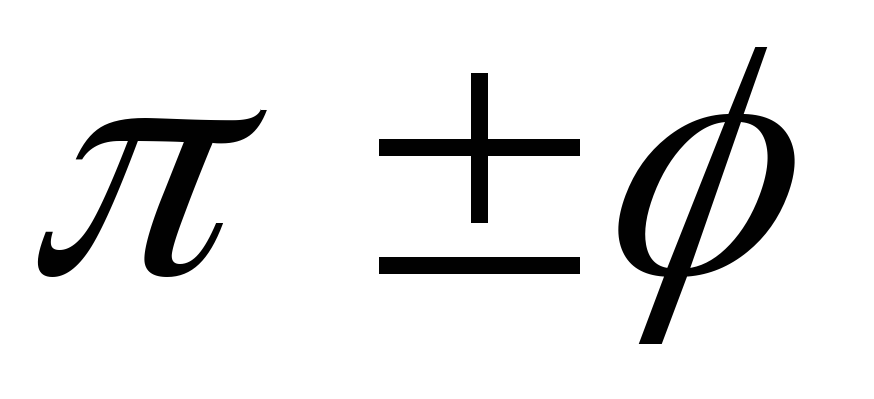 ,
,
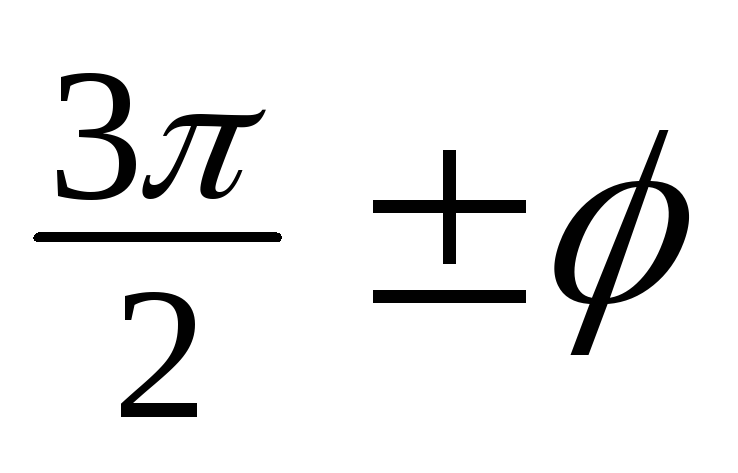 .
.
Доказательство.
Рассмотрим в плоскости
![]() единичную окружность и точку
единичную окружность и точку
![]() на данной окружности. Повернём систему
на угол
на данной окружности. Повернём систему
на угол
![]() ,
получив систему
,
получив систему
![]() ,
при этом точка
,
при этом точка
![]() перейдёт в точку
перейдёт в точку
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.
Известно, что
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Отсюда получаем, что
.
Отсюда получаем, что
![]() ,
,
![]() .
.
Аналогичным образом доказываются остальные формулы приведения. Ч.Т.Д.
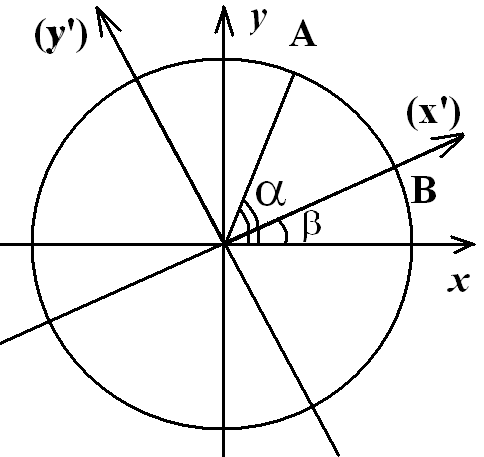
-
Формулы сложения
![]()
![]()
Доказательство.
В системе
![]() :
:
![]() ,
,
![]() .
Тогда
.
Тогда
![]()
![]()
Повернём оси
координат на угол
![]() ,
тогда в новой системе
,
тогда в новой системе
![]() :
:
![]() ,
,
![]() :
:
![]()
Таким образом
![]()
![]()
Отсюда
![]()
![]()
Заменим
![]() .
Тогда
.
Тогда
![]()
![]()
![]()
Отсюда
![]()
![]()
Ч.Т.Д.
-
Формулы двойного аргумента:
![]()
![]()
![]()
![]()
![]()
