
- •Элементарные функции Степень и степенная функция с натуральным показателем
- •40. , Если
- •Степень и степенная функция с целым отрицательным показателем
- •20. , Если
- •40. , Если
- •2. Если – чётное, то функция – чётная. Если – нечётное, то функция – нечётная.
- •Показательная функция с рациональным показателем
- •Понятие степени с иррациональным показателем.
- •Показательная функция с действительным показателем
- •Логарифмическая функция
- •Тригонометрические функции: синус, косинус.
Элементарные функции Степень и степенная функция с натуральным показателем
Определение.
Степенью
числа
![]() с натуральным показателем
с натуральным показателем
![]() называется
называется
![]()
Свойства степени:
10.
![]()
Доказательство.
По определению:
![]() и
и
![]() .
Тогда
.
Тогда
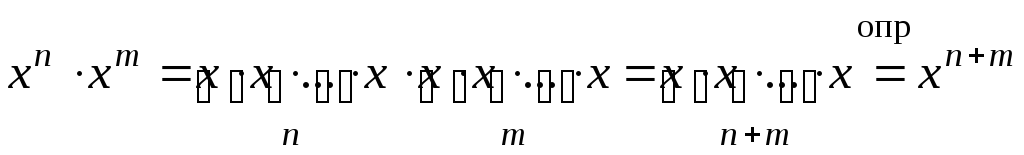 .
Ч.Т.Д.
.
Ч.Т.Д.
20.
![]() ,
если
,
если
![]() ,
,
![]()
30.
![]()
40. , Если
50.
![]()
Свойства 20 – 50 доказать самостоятельно.
Определение.
Степенная
функция с натуральным показателем
– это функция, определяемая формулой
![]() ,
,
![]() ,
,
![]() – переменная.
– переменная.
Свойства функции.
-
Областью определения функции
 является множество всех действительных
чисел:
является множество всех действительных
чисел:
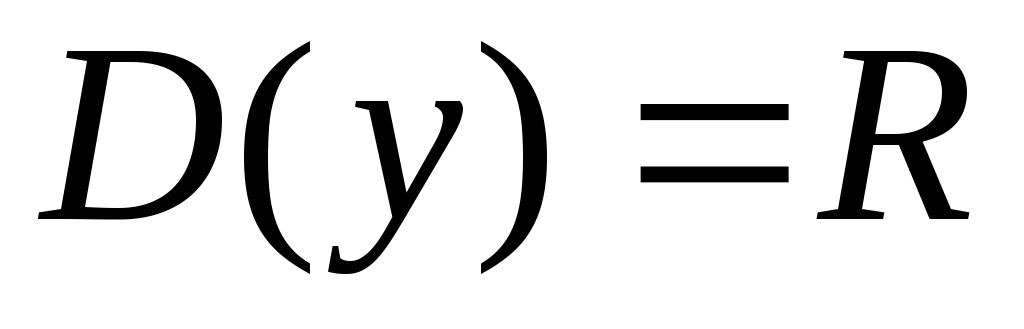 .
.
-
Если
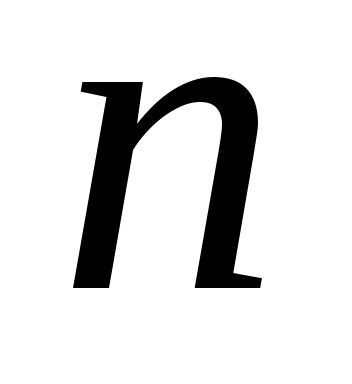 – чётное, то функция
– чётное, то функция
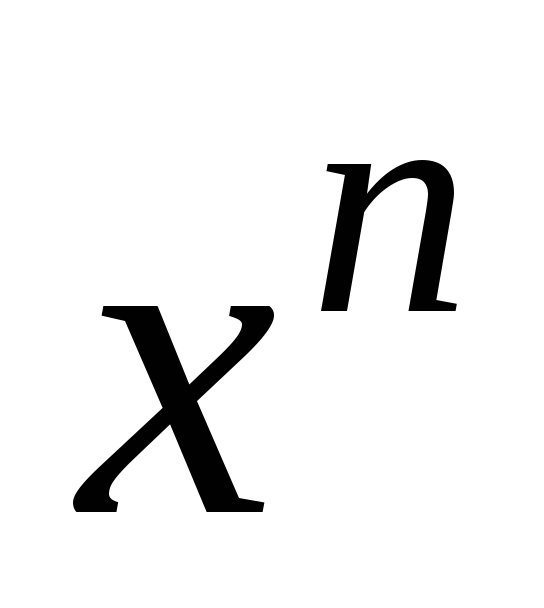 – чётная. Если
– чётная. Если
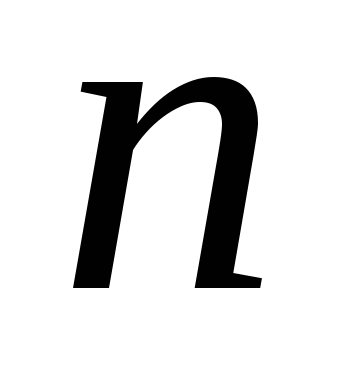 – нечётное, то функция
– нечётное, то функция
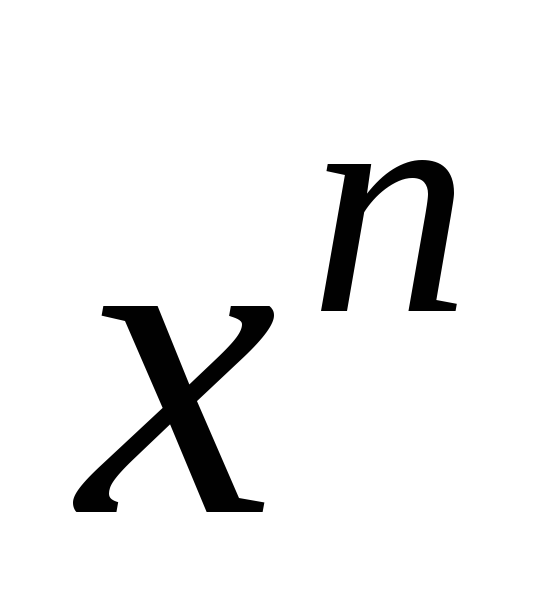 – нечётная.
– нечётная.
Доказательство.
Пусть
![]() – чётное, то есть
– чётное, то есть
![]() .
Тогда
.
Тогда
![]() .
.
![]()
Итак,
![]() при любом
при любом
![]() .
Следовательно, функция
.
Следовательно, функция
![]() – чётная. Аналогично доказывается, что
при нечётном
– чётная. Аналогично доказывается, что
при нечётном
![]() функция
функция
![]() – нечётная. Ч.Т.Д.
– нечётная. Ч.Т.Д.
-
Функция
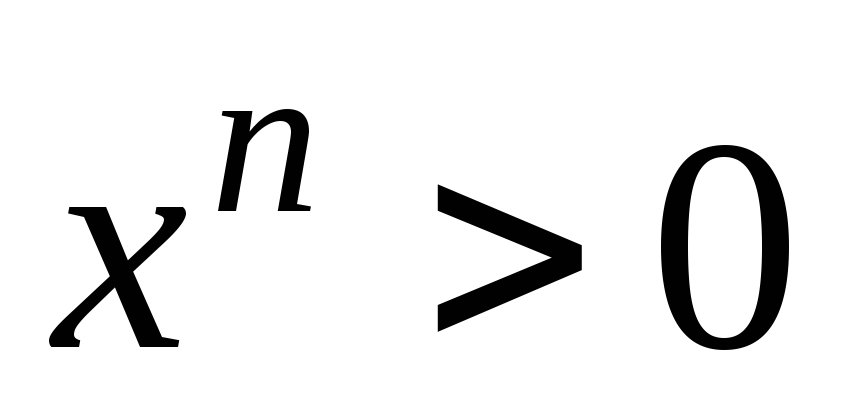 ,
если
,
если
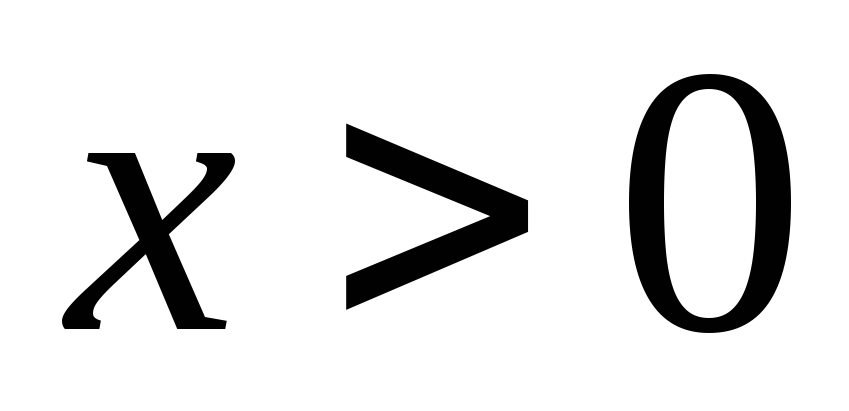 .
Если же
.
Если же
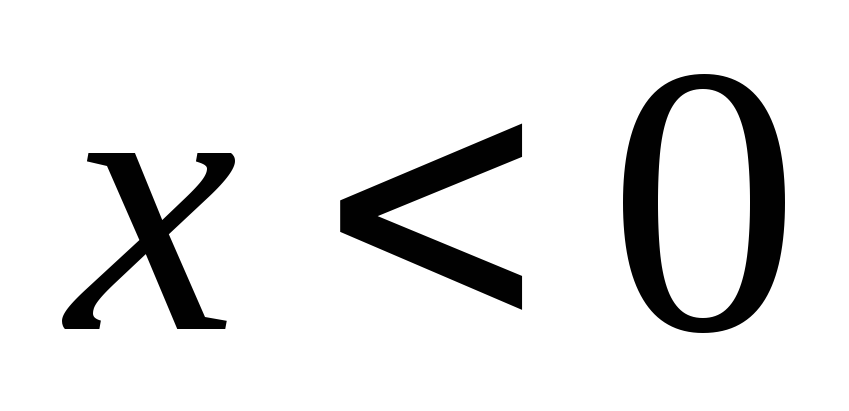 ,
то
,
то
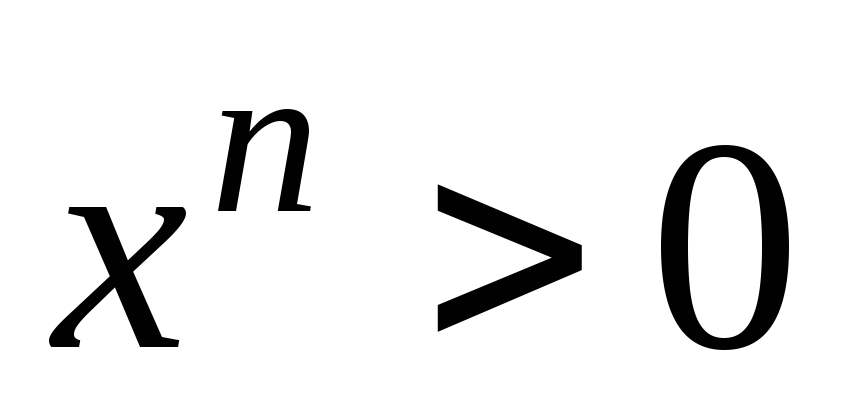 при чётном
при чётном
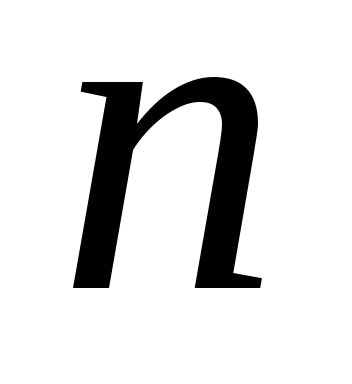 и
и
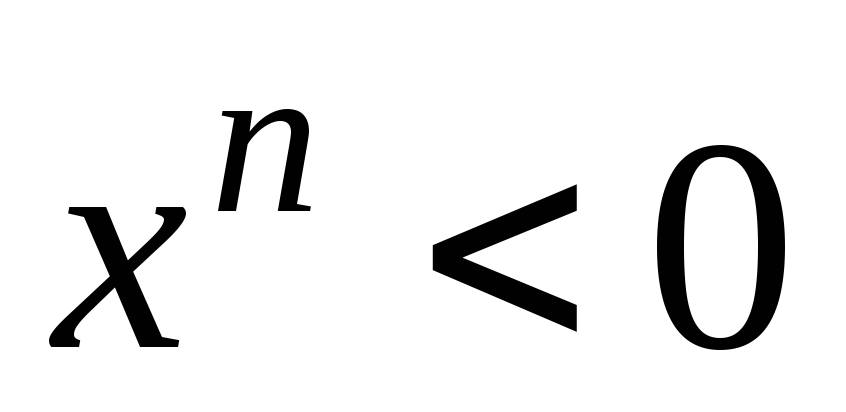 при нечётном
при нечётном
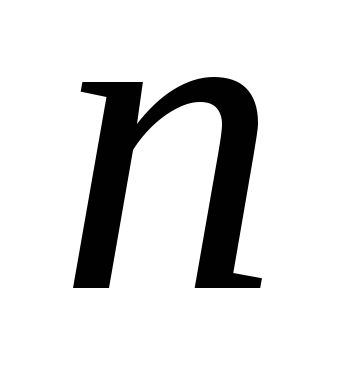 .
.
Доказательство.
Очевидно, что при
![]() и функция
и функция
![]() .
Докажем второе утверждение. Пусть
.
Докажем второе утверждение. Пусть
![]() ,
тогда
,
тогда
![]() .
В этом случае по первому утверждению
.
В этом случае по первому утверждению
![]() .
Отсюда получаем: при чётном
.
Отсюда получаем: при чётном
![]()
![]() ,
,
при нечётном
![]()
![]()
Ч.Т.Д.
-
Функция
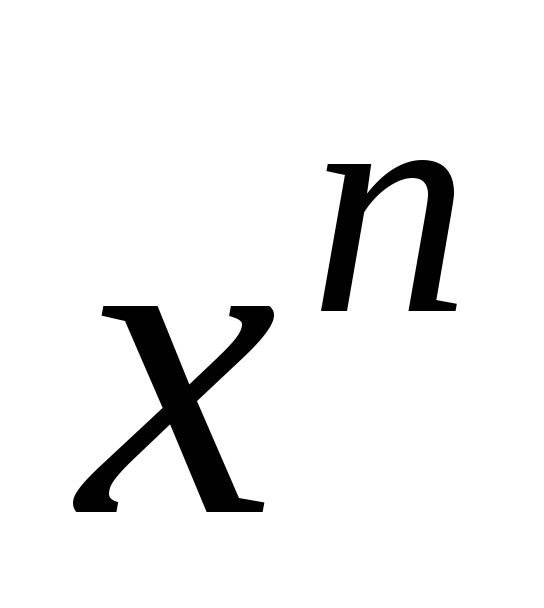 непрерывна на множестве всех действительных
чисел.
непрерывна на множестве всех действительных
чисел.
Доказательство.
Сначала покажем, что функция
![]() непрерывна на множестве
непрерывна на множестве
![]() .
Для этого достаточно показать, что
.
Для этого достаточно показать, что
![]() непрерывна в любой точке
непрерывна в любой точке
![]() .
По определению непрерывности в точке
надо доказать, что
.
По определению непрерывности в точке
надо доказать, что
![]() ,
то есть что
,
то есть что
![]() .
Возьмём любое
.
Возьмём любое
![]() и докажем что существует
и докажем что существует
![]() :
:
![]() :
:
![]() ,
то есть
,
то есть
![]() .
Очевидно, что для любого
.
Очевидно, что для любого
![]() можно взять
можно взять
![]() ,
так как из неравенства
,
так как из неравенства
![]() следует
следует
![]() .
.
Итак, функция
![]() непрерывна в любой точке множества
непрерывна в любой точке множества
![]() .
Тогда функция
.
Тогда функция
![]() непрерывна на множестве
непрерывна на множестве
![]() по теореме о непрерывности произведения
конечного числа непрерывных функций.
Ч.Т.Д.
по теореме о непрерывности произведения
конечного числа непрерывных функций.
Ч.Т.Д.
-
Если
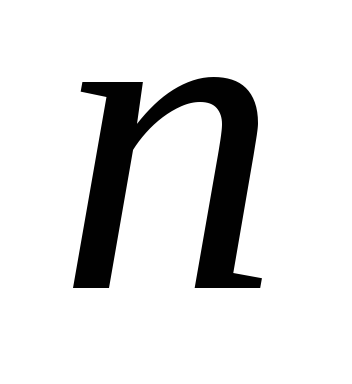 – чётное, то функция
– чётное, то функция
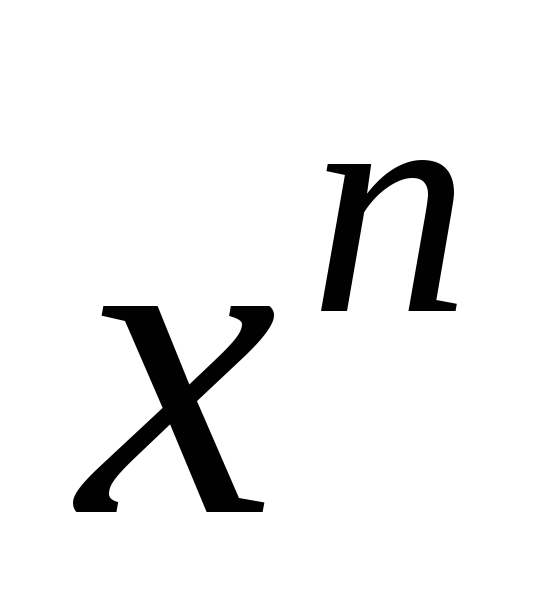 строго возрастает на промежутке
строго возрастает на промежутке
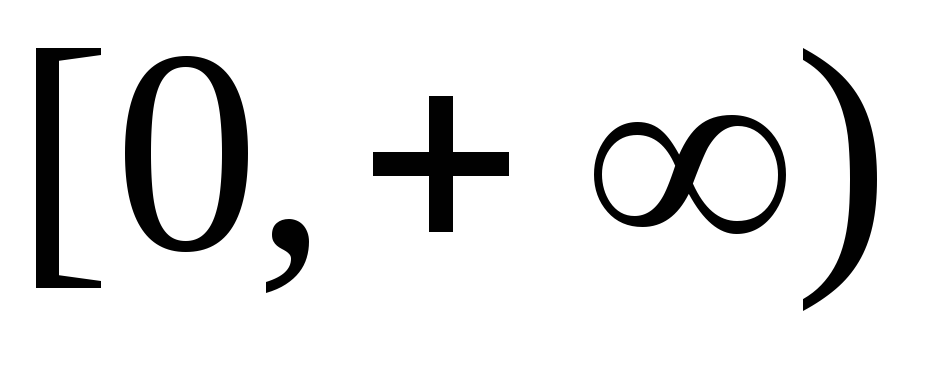 и строго убывает на промежутке
и строго убывает на промежутке
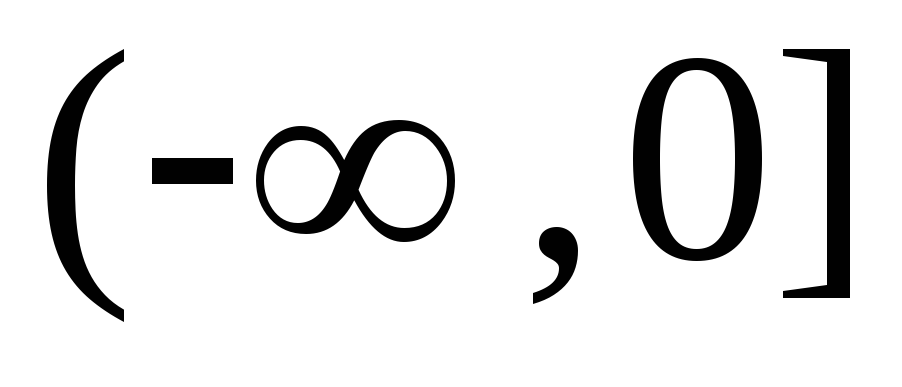 .
Если
.
Если
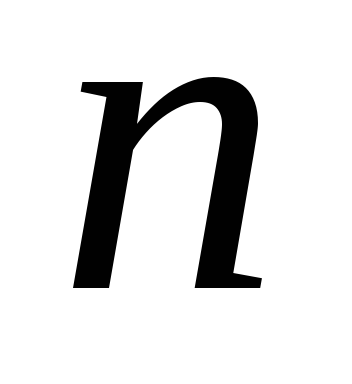 – нечётное, то функция
– нечётное, то функция
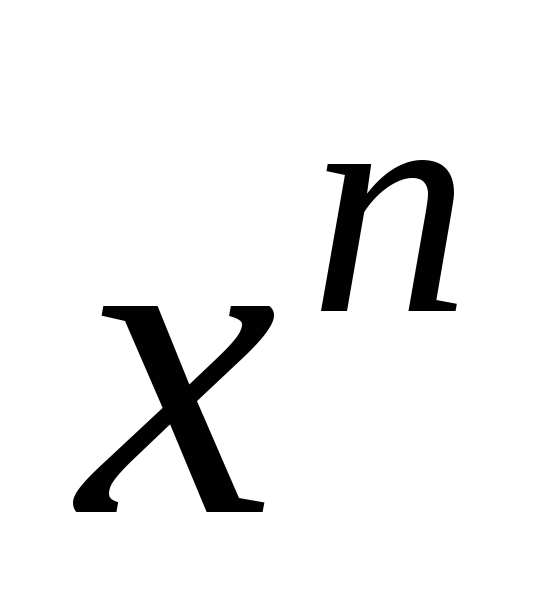 строго возрастает на интервале
строго возрастает на интервале
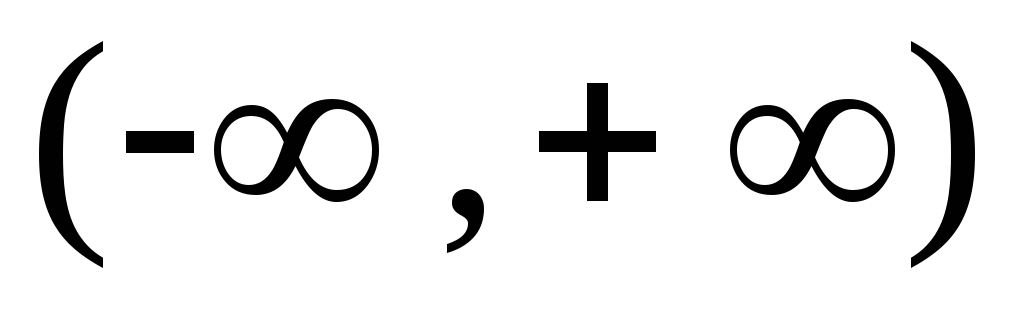 .
.
Доказательство.
Пусть
![]() – чётное. Покажем, что функция
– чётное. Покажем, что функция
![]() строго возрастает на промежутке
строго возрастает на промежутке
![]() .
Возьмём любые
.
Возьмём любые
![]() ,
то есть
,
то есть
![]() ,
,
![]() ,
причём
,
причём
![]() ,
и докажем, что
,
и докажем, что
![]() .
Рассмотрим равенство
.
Рассмотрим равенство
![]()
![]() (*)
(*)
Так как
![]() ,
то
,
то
![]() .
Так как
.
Так как
![]() ,
,
![]() ,
то
,
то
![]() .
Следовательно, правая часть равенства
(*) положительна
.
Следовательно, правая часть равенства
(*) положительна
-
Графики всех функций
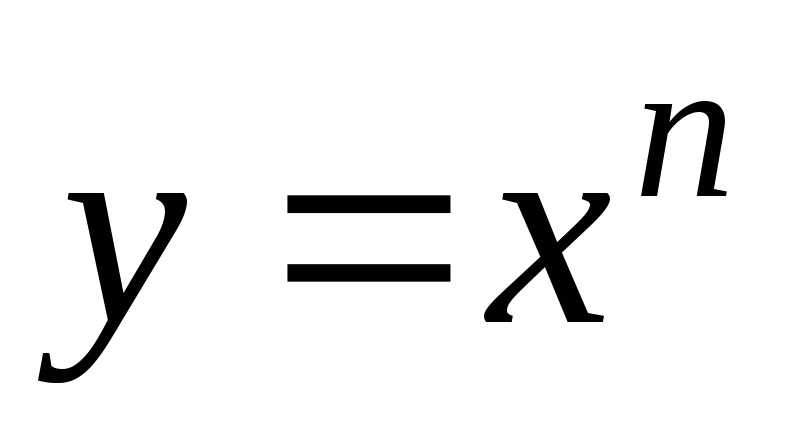 проходят через точки
проходят через точки
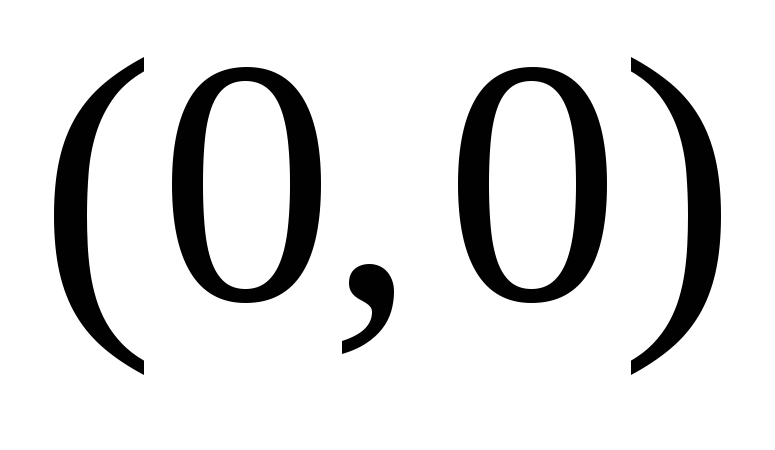 и
и
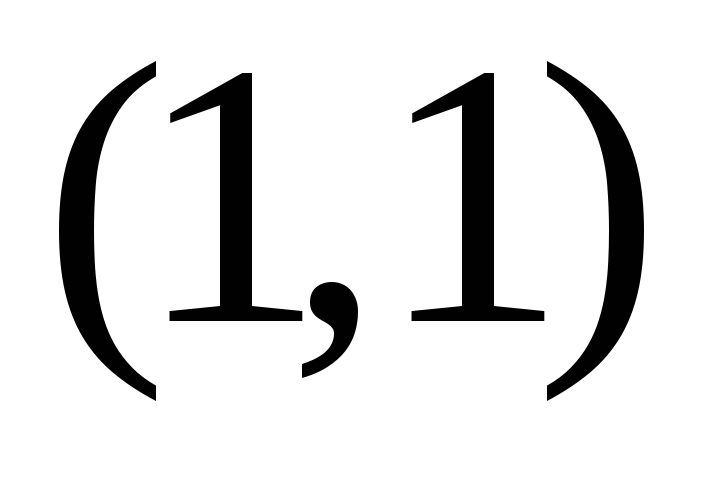 .
.
-
Если
 ,
то
,
то
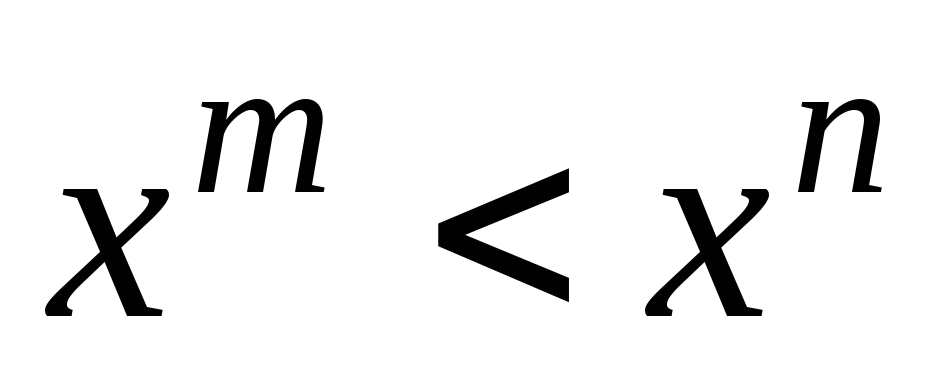 для любого
для любого
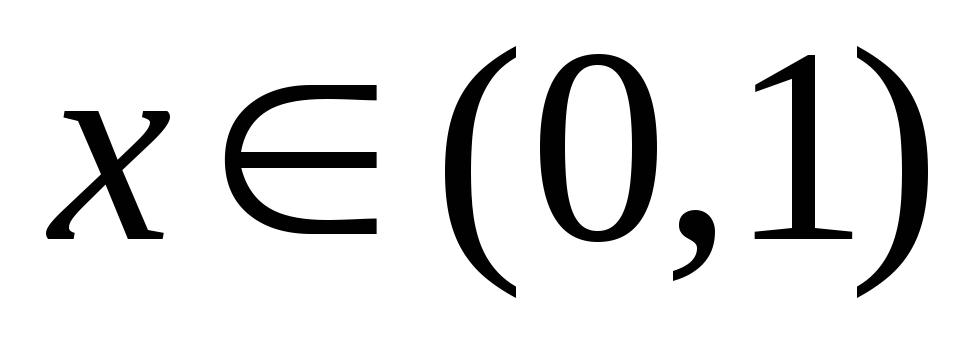 и
и
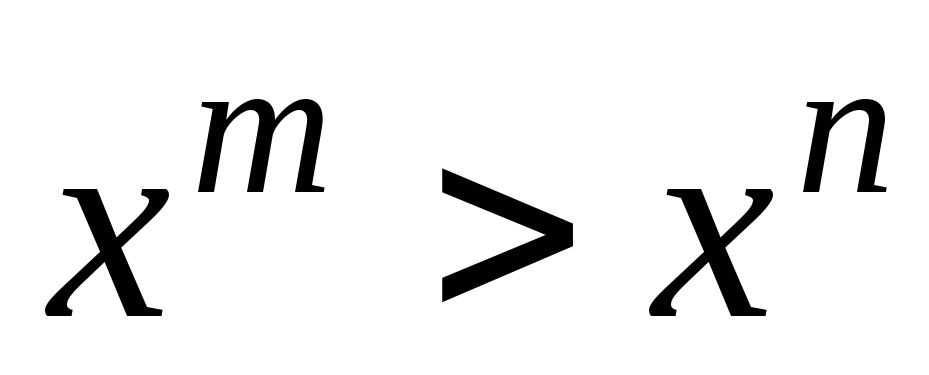 для любого
для любого
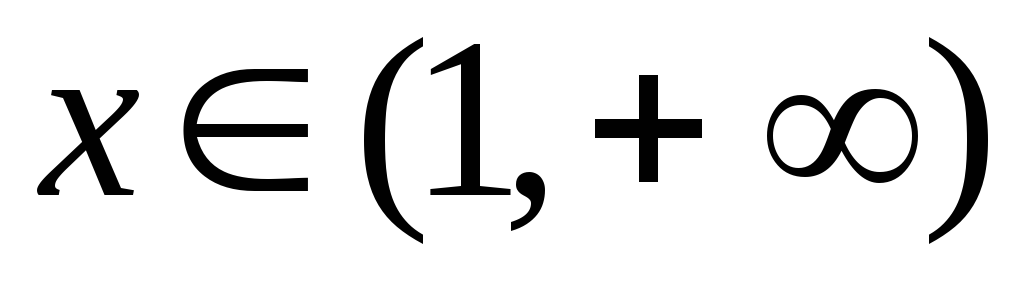 .
.
Доказательство.
Геометрически это означает, что на
![]() график степенной функции с большим
показателем лежит ниже графика степенной
функции с меньшим показателем. А в
интервале
график степенной функции с большим
показателем лежит ниже графика степенной
функции с меньшим показателем. А в
интервале
![]() – наоборот.
– наоборот.
Пусть
![]() .
Рассмотрим отношение
.
Рассмотрим отношение
![]() ,
при этом
,
при этом
![]() .
В силу строго возрастания степенной
функции с натуральным показателем из
неравенства
.
В силу строго возрастания степенной
функции с натуральным показателем из
неравенства
![]() следует неравенство
следует неравенство
![]() ,
то есть
,
то есть
![]() .
Поэтому
.
Поэтому
![]() .
Умножая обе части неравенства на
.
Умножая обе части неравенства на
![]() (по свойству 3), получаем
(по свойству 3), получаем
![]() для
для
![]() .
.
Пусть
![]() .
Из неравенства
.
Из неравенства
![]() получаем
получаем
![]() .
Следовательно,
.
Следовательно,
![]() .
Ч.Т.Д.
.
Ч.Т.Д.
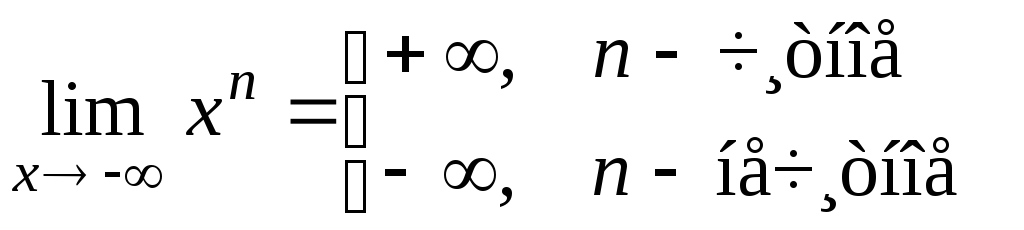
Доказательство.
Напомним определение:
![]() ,
если для любого
,
если для любого
![]() существует
существует
![]() ,
такое что для любых
,
такое что для любых
![]() выполняется неравенство
выполняется неравенство
![]() ,
в нашем случае
,
в нашем случае
![]() .
.
Сначала докажем,
что
![]() .
Для этого возьмём любое
.
Для этого возьмём любое
![]() и
покажем, что существует
и
покажем, что существует
![]() ,
такое что для любых
,
такое что для любых
![]() выполняется неравенство
выполняется неравенство
![]() .
Очевидно, что
.
Очевидно, что
![]() (тогда из неравенства
(тогда из неравенства
![]() следует неравенство
следует неравенство
![]() ).
).
Получили, что
![]() – бесконечно большая функция при
– бесконечно большая функция при
![]() .
Тогда
.
Тогда
![]() – положительная бесконечно большая
функция при
– положительная бесконечно большая
функция при
![]() по теореме о произведении бесконечно
больших функций, то есть
по теореме о произведении бесконечно
больших функций, то есть
![]() .
.
Случай, когда
![]() доказывается с помощью замены
доказывается с помощью замены
![]() .
.
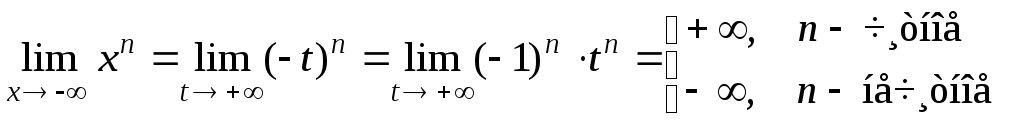
Ч.Т.Д.
-
Множеством значений функции
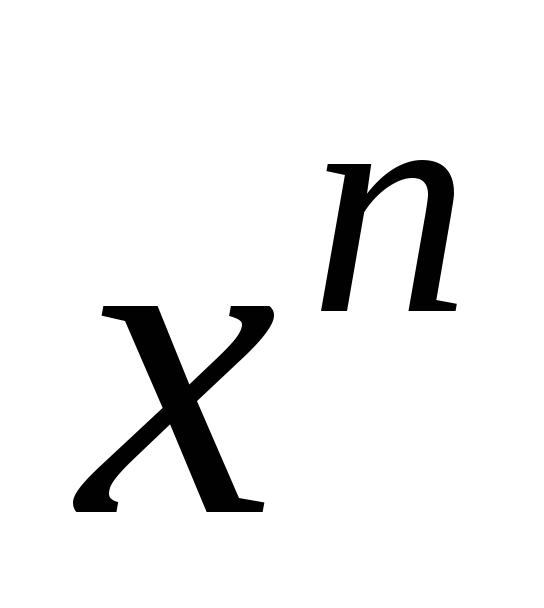 является промежуток
является промежуток
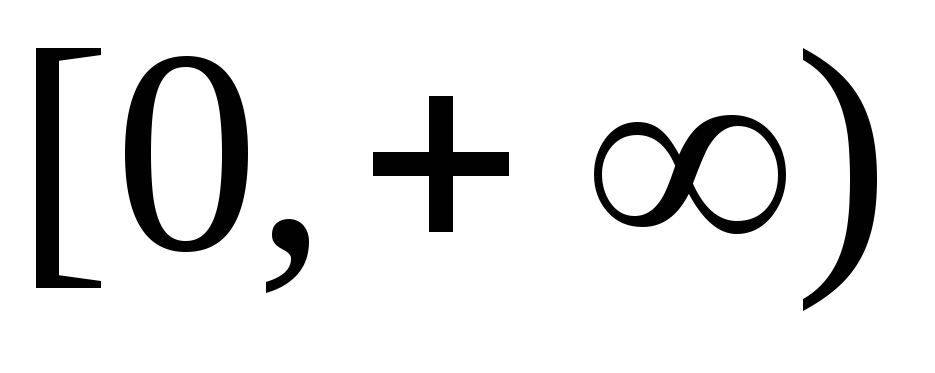 ,
если
,
если
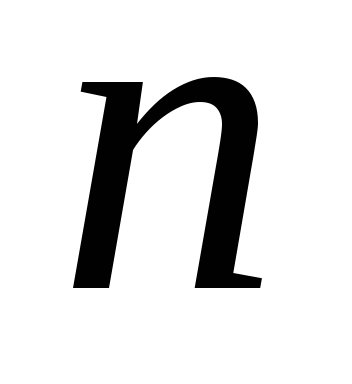 – чётное, и
– чётное, и
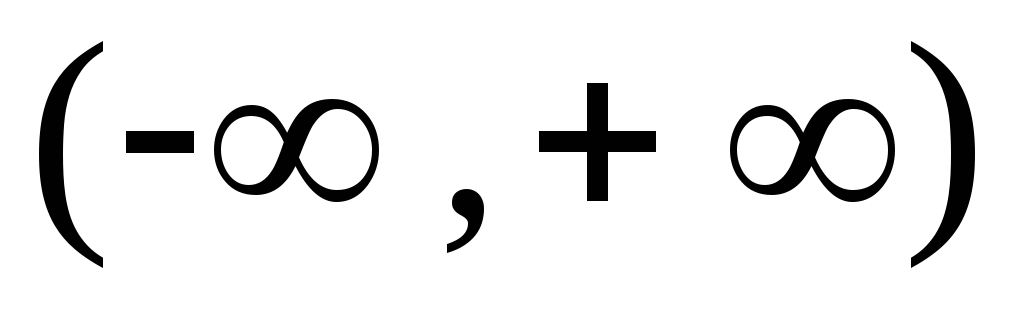 ,
если
,
если
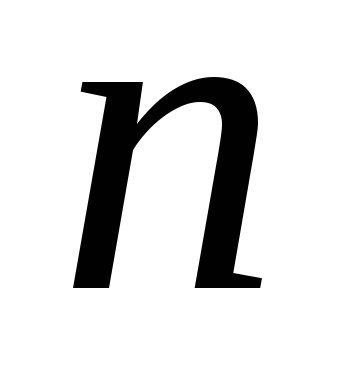 – нечётное.
– нечётное.
Доказательство.
Пусть
![]() – чётное. Уже известно, что для любого
– чётное. Уже известно, что для любого
![]()
![]() .
Следовательно, значение функции попадает
в промежуток
.
Следовательно, значение функции попадает
в промежуток
![]() .
Докажем, что эти значения сплошь заполняют
промежуток, то есть покажем, что для
любого
.
Докажем, что эти значения сплошь заполняют
промежуток, то есть покажем, что для
любого
![]() существует
существует
![]() ,
такое что
,
такое что
![]() .
.
Очевидно, что для
![]() такое
такое
![]() уже найдено, это
уже найдено, это
![]() ,
так как
,
так как
![]() .
.
Пусть
![]() .
Так как
.
Так как
![]() ,
то по определению бесконечного предела
функции для любого
,
то по определению бесконечного предела
функции для любого
![]() ,
а значит и для
,
а значит и для
![]() найдётся
найдётся![]() ,
такое что для любых
,
такое что для любых
![]() выполняется неравенство
выполняется неравенство
![]() .
Поэтому найдётся хотя бы одно
.
Поэтому найдётся хотя бы одно
![]() ,
такое что
,
такое что
![]() .
Обозначим
.
Обозначим
![]() .
Тогда
.
Тогда
![]() .
.
Рассмотрим функцию
![]() на отрезке
на отрезке
![]() .
Функция непрерывная на этом отрезке и
принимает на его концах значения:
.
Функция непрерывная на этом отрезке и
принимает на его концах значения:
![]() ,
,
![]() .
Тогда по теореме о промежуточном значении
функции, непрерывной на отрезке получаем,
что для числа
.
Тогда по теореме о промежуточном значении
функции, непрерывной на отрезке получаем,
что для числа
![]() ,
заключённого между
,
заключённого между
![]() и
и
![]() ,
найдётся
,
найдётся
![]() ,
лежащее внутри отрезка
,
лежащее внутри отрезка
![]() ,
такое что
,
такое что
![]() .
.
Пусть
![]() – нечётное. Возьмём любое
– нечётное. Возьмём любое
![]() и покажем, что существует
и покажем, что существует
![]() ,
такое что
,
такое что
![]() .
Если окажется, что
.
Если окажется, что
![]() ,
то существует
,
то существует
![]() ,
такое что
,
такое что
![]() (доказано выше). Пусть
(доказано выше). Пусть
![]() ,
тогда
,
тогда
![]() ,
то есть
,
то есть
![]() ,
а для такого промежутка уже доказано,
что существует
,
а для такого промежутка уже доказано,
что существует
![]() ,
такое что
,
такое что
![]() ,
откуда
,
откуда
![]() .
Так как при нечетном
.
Так как при нечетном
![]() функция
функция
![]() является нечётной, то
является нечётной, то
![]() .
Тогда можно сказать, что для
.
Тогда можно сказать, что для
![]() нашлось
нашлось
![]() ,
такое что
,
такое что
![]() .
Ч.Т.Д.
.
Ч.Т.Д.
