
- •Элементарные функции Степень и степенная функция с натуральным показателем
- •40. , Если
- •Степень и степенная функция с целым отрицательным показателем
- •20. , Если
- •40. , Если
- •2. Если – чётное, то функция – чётная. Если – нечётное, то функция – нечётная.
- •Показательная функция с рациональным показателем
- •Понятие степени с иррациональным показателем.
- •Показательная функция с действительным показателем
- •Логарифмическая функция
- •Тригонометрические функции: синус, косинус.
Степень и степенная функция с целым отрицательным показателем
Определение.
Степенью
числа
![]() с показателем
с показателем
![]() (
(![]() )
называется число
)
называется число
![]() ,
то есть
,
то есть
![]() .
.
Свойства степени.
10.
![]()
20. , Если
Доказательство.
Пусть
![]() ,
тогда
,
тогда
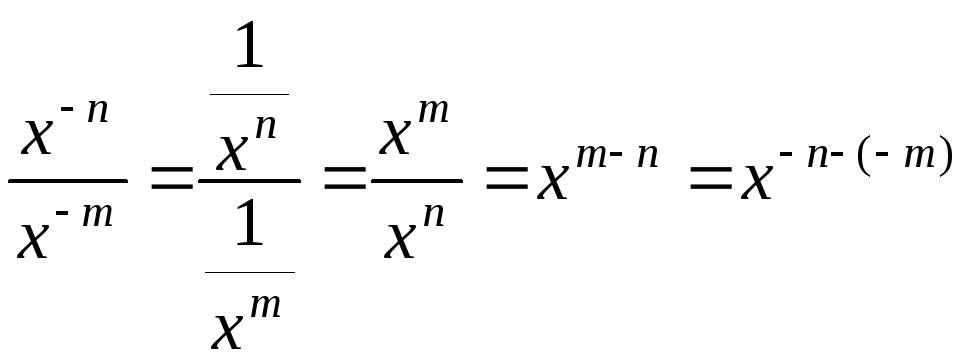 .
Если
.
Если
![]() ,
то
,
то
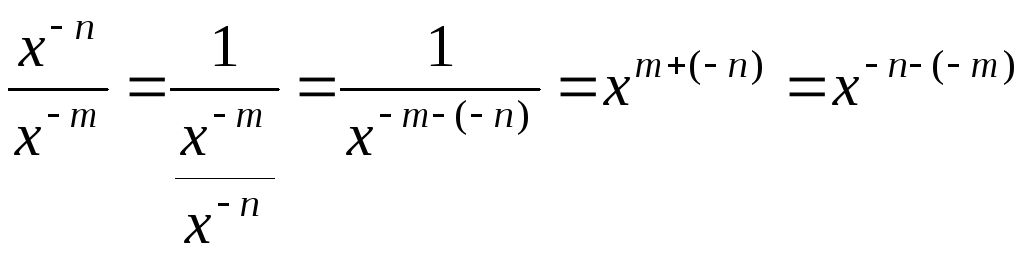 .
Ч.Т.Д,
.
Ч.Т.Д,
30.
![]()
40. , Если
50.
![]()
Определение.
Степенной
функцией с целым отрицательным показателем
называется функция вида
![]() ,
где
,
где
![]() ,
,
![]() – переменная.
– переменная.
Свойства функции.
1. Функция
определена для любого
![]() ,
кроме
,
кроме
![]() .
.
2. Если – чётное, то функция – чётная. Если – нечётное, то функция – нечётная.
Доказательство
следует из аналогичного свойства
знаменателя дроби
![]() .
.
3. Если
![]() ,
то
,
то
![]() .
Если
.
Если
![]() ,
то
,
то
![]() при нечётном
при нечётном
![]() и
и
![]() при чётном
при чётном
![]() .
.
Свойство следует
из свойства 3 для функции
![]() .
.
4. Функция
![]() непрерывна на множестве действительных
чисел, кроме
непрерывна на множестве действительных
чисел, кроме
![]() ,
при этом
,
при этом
![]() и
и
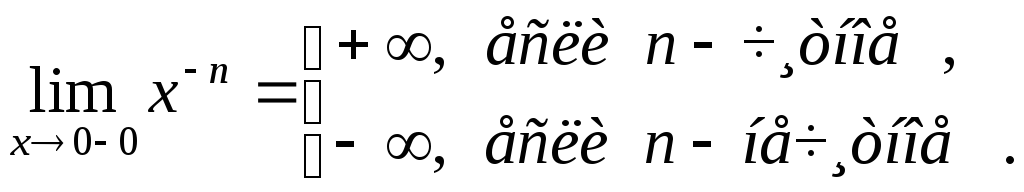
Доказательство.
Так как
![]() ,
то применим теорему о непрерывности
частного.
,
то применим теорему о непрерывности
частного.
![]() ,
где функция
,
где функция
![]() непрерывна на
непрерывна на
![]() как постоянная функция,
как постоянная функция,
![]() – непрерывна на
– непрерывна на
![]() (по свойству 4 степенной функции с
натуральным показателем), при этом
(по свойству 4 степенной функции с
натуральным показателем), при этом
![]() в точке
в точке
![]() .
Тогда функция
.
Тогда функция
![]() непрерывна на множестве всех действительных
чисел, кроме
непрерывна на множестве всех действительных
чисел, кроме
![]() .
.
![]() – точка разрыва.
Установим её тип:
– точка разрыва.
Установим её тип:
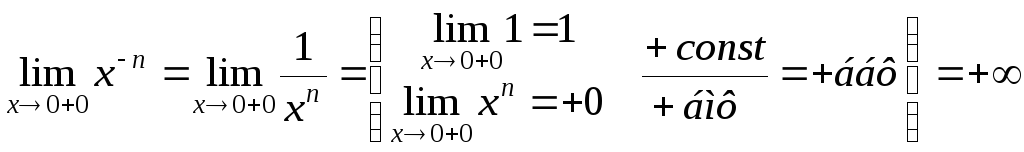 ,
,

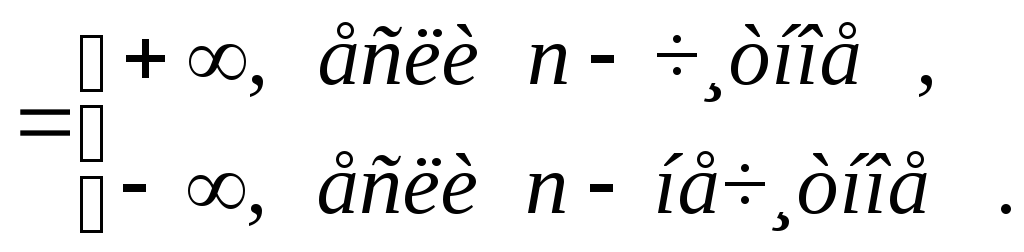
Ч.Т.Д.
5. Функция
![]() строго убывает на интервале
строго убывает на интервале
![]() ,
а на интервале
,
а на интервале
![]() строго возрастает при чётном
строго возрастает при чётном
![]() и строго убывает при нечётном
и строго убывает при нечётном
![]() .
.
Доказательство.
Возьмем любые
![]() ,
при этом
,
при этом
![]() .
Покажем, что
.
Покажем, что
![]() .
.
В силу возрастания
функции
![]() на
на
![]() из неравенства
из неравенства
![]() следует, что
следует, что
![]() .
Разделим обе части неравенства на
.
Разделим обе части неравенства на
![]() .
Получим
.
Получим
![]() .
Отсюда
.
Отсюда
![]() .
.
Возьмем любые
![]() ,
при этом
,
при этом
![]() .
Тогда
.
Тогда
![]() ,
то есть
,
то есть
![]() .
Тогда по первому случаю из неравенства
.
Тогда по первому случаю из неравенства
![]() следует, что
следует, что
![]() . (*)
. (*)
Если
![]() – чётное, то из (*) следует
– чётное, то из (*) следует
![]() ,
то есть функция возрастает на
,
то есть функция возрастает на
![]() .
Если
.
Если
![]() – нечётное, то из (*) следует
– нечётное, то из (*) следует
![]() или
или
![]() ,
то есть функция убывает на
,
то есть функция убывает на
![]() .
Ч.Т.Д.
.
Ч.Т.Д.
6.
График функции пройдет через точку
![]() .
.
7.
Если
![]() ,
то
,
то
![]() при
при
![]() и
и
![]() при
при
![]() .
.
Доказательство.
Пусть
![]() и
и
![]() .
По свойству 7 степенной функции с
натуральным показателем
.
По свойству 7 степенной функции с
натуральным показателем
![]() .
Разделив обе части неравенства на
.
Разделив обе части неравенства на
![]() ,
получим
,
получим
![]() .
Отсюда
.
Отсюда
![]() .
.
Аналогично
доказывается для
![]() .
Ч.Т.Д.
.
Ч.Т.Д.
8.
![]() .
.
Доказательство.
![]() .
.
9.
Если
![]() – чётное, то множеством значений функции
– чётное, то множеством значений функции
![]() является интервал
является интервал
![]() ,
если
,
если
![]() – нечётное, то
– нечётное, то
![]() .
.
Доказательство.
Пусть
![]() – чётное. Тогда для любого
– чётное. Тогда для любого
![]()
![]() ,
то есть значения функции попадают в
,
то есть значения функции попадают в
![]() .
Покажем, что значения этой функции
сплошь заполняют данный промежуток.
.
Покажем, что значения этой функции
сплошь заполняют данный промежуток.
Для этого возьмём
любое
![]() и покажем, что найдётся хотя бы одно
и покажем, что найдётся хотя бы одно
![]() ,
такое что
,
такое что
![]() .
По свойству о множестве значений
степенной функции с натуральным
показателем при чётном
.
По свойству о множестве значений
степенной функции с натуральным
показателем при чётном
![]() для числа
для числа
![]() существует
существует
![]() ,
такое что
,
такое что
![]() .
Отсюда
.
Отсюда
![]() ,
то есть
,
то есть
![]() .
.
Если
![]() – нечётное, то доказательство аналогично.
Ч.Т.Д.
– нечётное, то доказательство аналогично.
Ч.Т.Д.
Показательная функция с рациональным показателем
Определение.
Показательной
функцией с рациональным показателем
называется функция вида
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() – переменная.
– переменная.
Свойства.
-
Функция определена на множестве рациональных чисел.
-
Для любого рационального числа
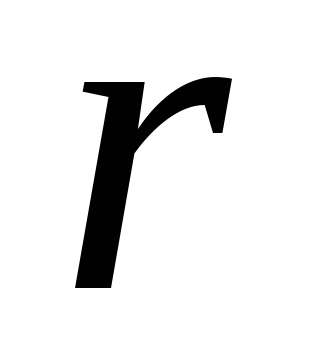 :
:
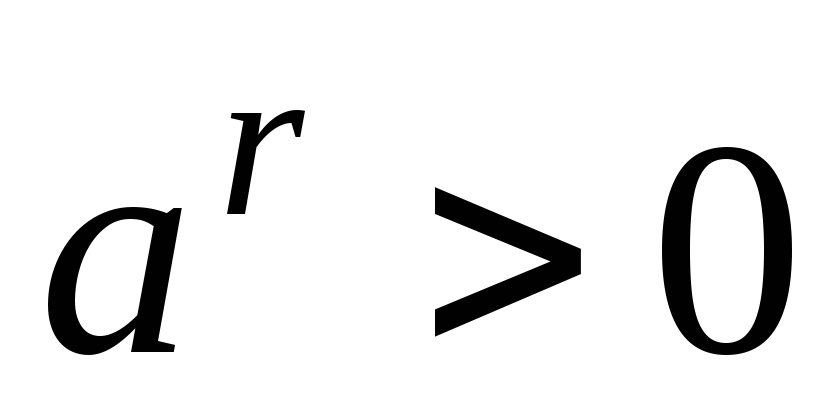 .
.
Доказательство.
Пусть
![]() .
По свойству возрастания степенной
функции
.
По свойству возрастания степенной
функции
![]() на множестве положительных чисел из
неравенства
на множестве положительных чисел из
неравенства
![]() получаем
получаем
![]() .
Отсюда
.
Отсюда
![]() .
Пусть
.
Пусть
![]() .
Тогда
.
Тогда
![]() ,
где
,
где
![]() .
Отсюда
.
Отсюда
![]() .
Пусть
.
Пусть
![]() .
Отсюда
.
Отсюда
![]() ,
то есть
,
то есть
![]() .
Ч.Т.Д.
.
Ч.Т.Д.
-
Если
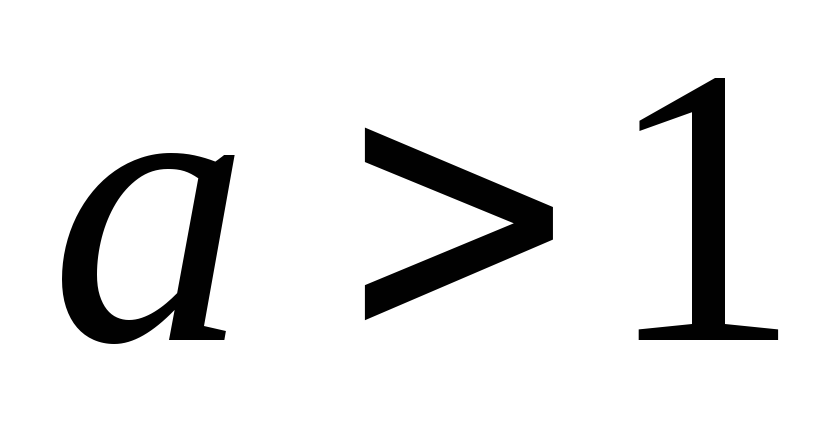 ,
то
,
то
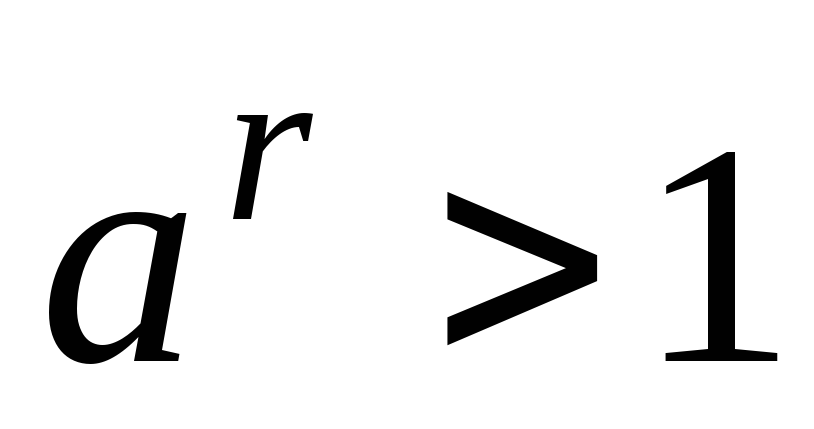 при
при
 и
и
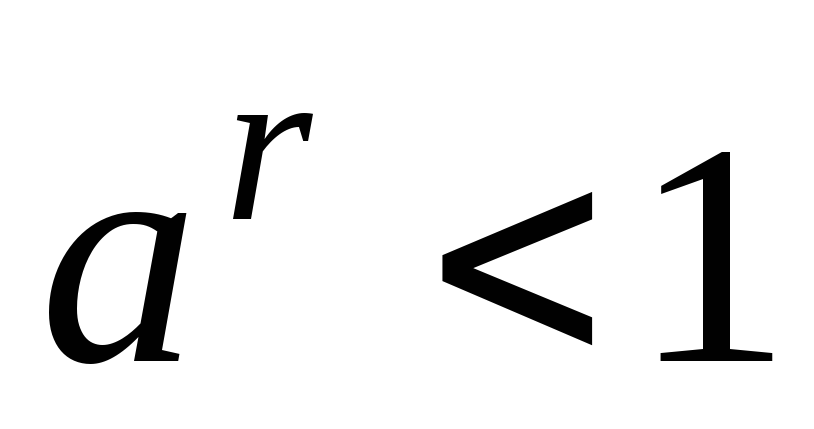 при
при
 .
Если
.
Если
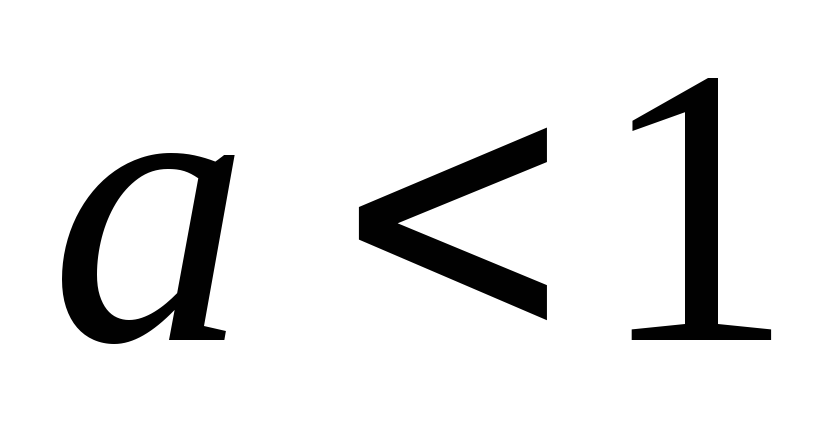 ,
то
,
то
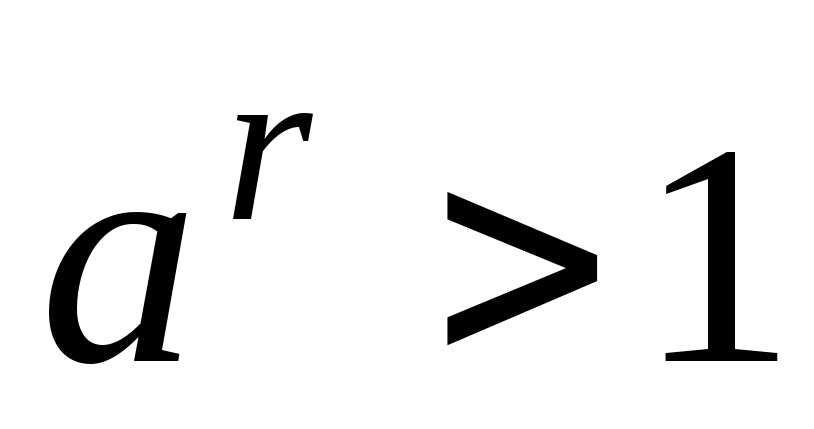 при
при
 и
и
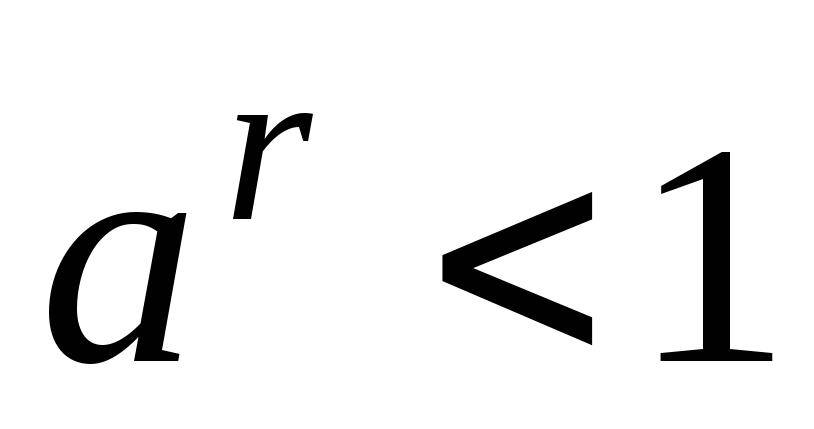 при
при
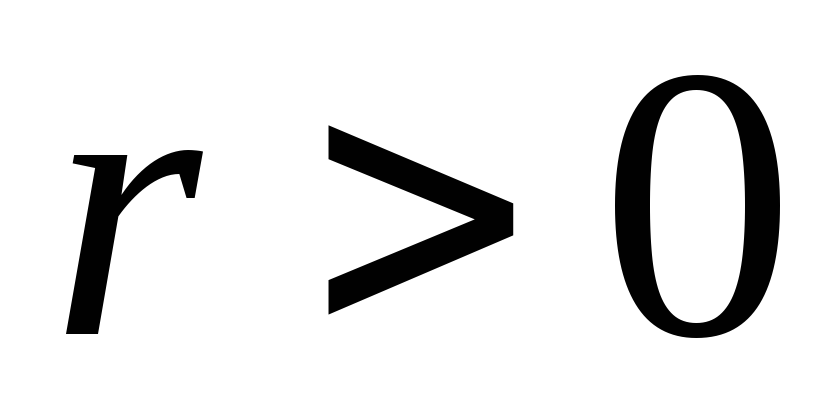 .
.
Доказательство.
Пусть
![]() .
По свойству возрастания степенной
функции
.
По свойству возрастания степенной
функции
![]() на промежутке
на промежутке
![]() при
при
![]() из неравенства
из неравенства
![]() получаем
получаем
![]() .
Отсюда
.
Отсюда
![]() .
Если
.
Если
![]() ,
то функция
,
то функция
![]() убывает на промежутке
убывает на промежутке
![]() .
Поэтому из неравенства
.
Поэтому из неравенства
![]() получаем
получаем
![]() ,
то есть
,
то есть
![]() .
.
Если
![]() ,
то доказательство аналогично. Ч.Т.Д.
,
то доказательство аналогично. Ч.Т.Д.
-
При
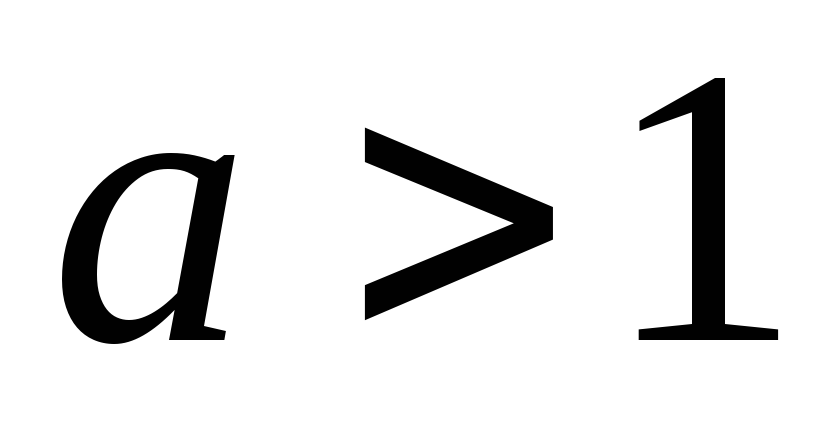 функция
функция
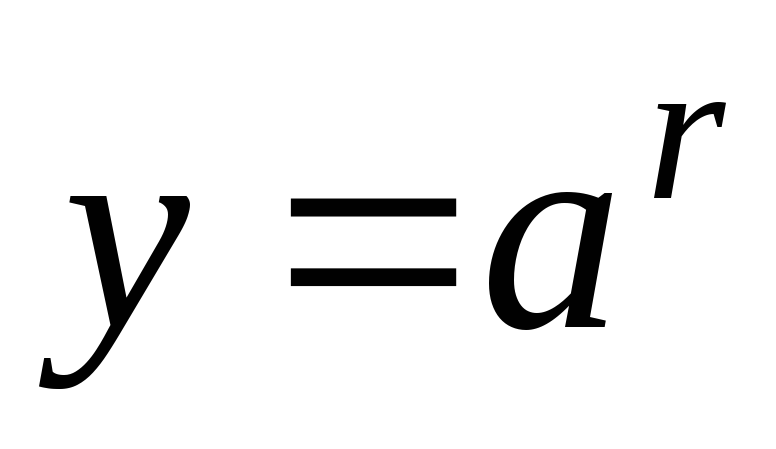 строго возрастает на множестве
рациональных чисел. При
строго возрастает на множестве
рациональных чисел. При
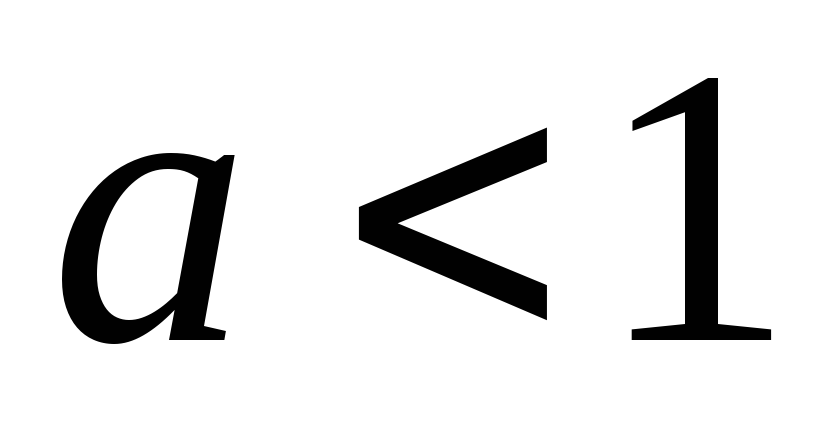 функция
функция
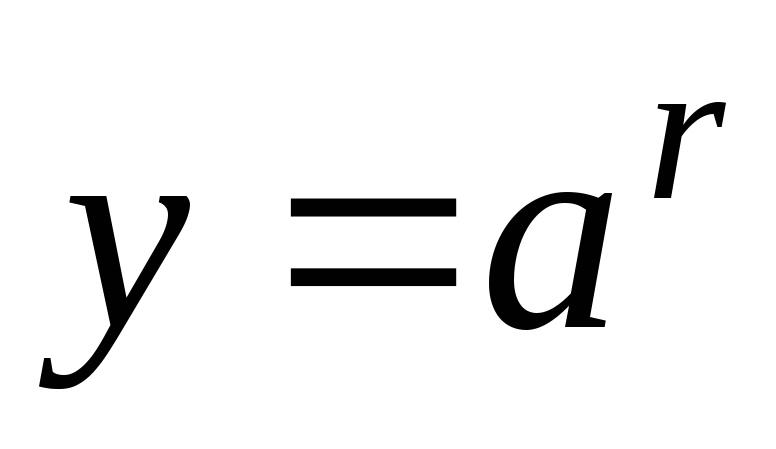 строго убывает на том же множестве.
строго убывает на том же множестве.
Доказательство.
-
Какова бы на была последовательность рациональных чисел
 ,
сходящаяся к нулю, то есть
,
сходящаяся к нулю, то есть
 ,
имеет место равенство
,
имеет место равенство
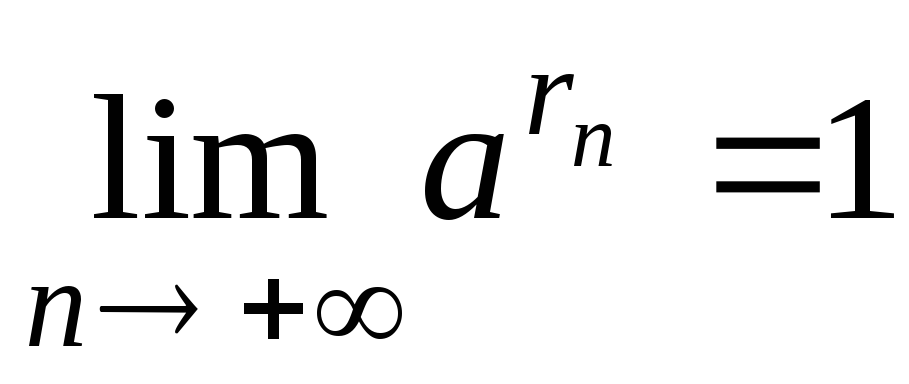 .
.
-
Для любой последовательности рациональных чисел
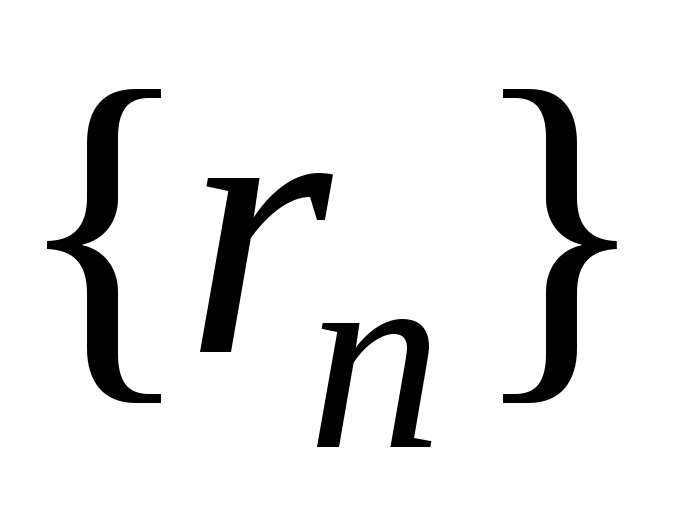 ,
стремящейся к
,
стремящейся к
 ,
имеет место равенство
,
имеет место равенство
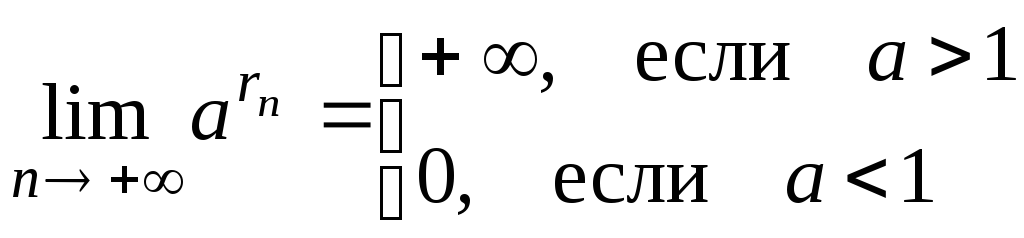
Замечание.
Ранее доказательство
![]() проводилось с помощью неравенства
Бернулли. Возникает вопрос: почему
нельзя провести данное доказательство
с помощью логарифмирования?
проводилось с помощью неравенства
Бернулли. Возникает вопрос: почему
нельзя провести данное доказательство
с помощью логарифмирования?
Проанализируем
этот способ. Цель: для любого
![]() найти номер
найти номер
![]() ,
такой что для любого натурального
,
такой что для любого натурального
![]() выполняется неравенство
выполняется неравенство
![]() . (*)
. (*)
Пусть
![]() .
Тогда неравенство (*) примет вид
.
Тогда неравенство (*) примет вид
![]() .
Отсюда
.
Отсюда
![]() .
Если прологарифмируем по основанию
.
Если прологарифмируем по основанию
![]() последнее неравенство, то получим
последнее неравенство, то получим
![]() .
Тогда
.
Тогда
![]() .
Обозначим
.
Обозначим
![]() .
.
Вопрос: почему это незаконно при построении строгой теории элементарных функций.
