34.Квантование сигналов при наличии помех

В различных условиях на квантуемый сигнал всегда воздействует помеха. Поэтому целесообразно минимальный шаг квантования выбирать с учётом вероятностных характеристик этой помехи.

Предположим, что помеха аддитивна. Тогда мгновенное значение сигнала , которое ранее попадала в й шаг квантования и которое сопоставлялось с уровнем квантования , в результате действия помехи примет значение и может быть поставлено в соответствие другому уровню квантования . такой исход приведёт к искажению информации и вероятность его не должна превышать допустимого значения.

Обозначим через условную вероятность сопоставления значения уровню квантования вместо уровня при условии, что принадлежит му шагу квантования. При наличии помехи , а .

Полная вероятность того, что величина останется в пределах го шага

.

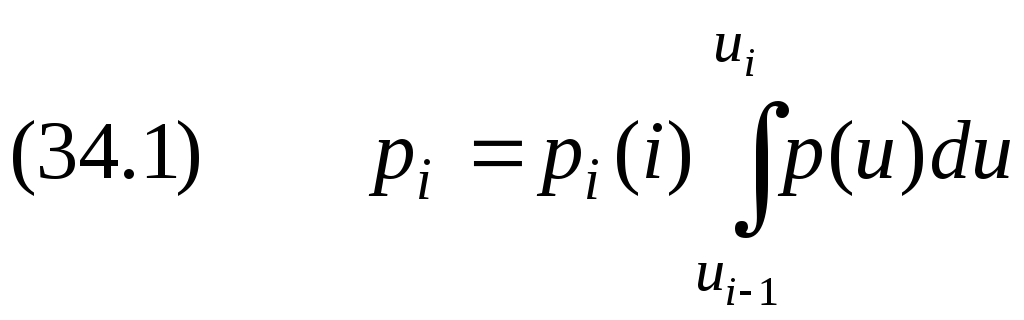Вероятность можно найти также, используя плотность вероятности системы двух случайных величин и :

,

где область интегрирования.

Так как нами учитываются мгновенные значения сигнала, которые принадлежат му шагу квантования, границами интегрирования по являются значения и . Верхняя и нижняя границы по определяются из условия и помехи не должны выйти за пределы го шага квантования:

,

откуда

.

Таким образом, область интегрирования представляет собой параллелограмм (рис. ).

Рис.

Считая помеху некоррелированной с сигналом, запишем

,

где плотность распределения помехи.

Ограничимся далее случаем равномерного квантования сигнала, мгновенные значения которого в диапазоне от до распределены равномерно, т.е.

.

Методику определения рассмотрим в предположении воздействия помехи, распределенной по закону равномерной плотности, а затем перейдём к практически важному случаю воздействия помехи с нормальным законом распределения.

Итак,

где амплитуда помехи, симметричной относительно мгновенного значения сигнала.

При указанных условиях результаты расчёта инвариантны относительно шага квантования и зависят от соотношения и .

Определим при . Область интегрирования (рис. ) разбиваем на отдельные участки и проставляем пределы интегрирования с учётом того, что знаменатель выражения (34.4) равен

.

Рис.

Тогда

Построив области интегрирования, тем же путём можно найти при и :

при ;

при .

На рис. представлен график , из которого, в частности, следует, что нецелесообразно выбирать меньше , так как при резко возрастает вероятность неправильного квантования сигнала.

Аналогично рассчитывают зависимость (рис. )

для воздействия на сигнал помехи, распределенной по нормальному закону

где среднеквадратическое отклонение помехи .

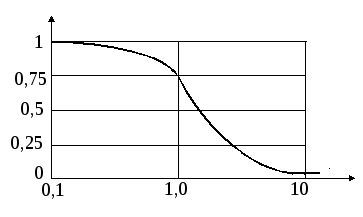
Рис.

Рис.

Сравнение двух последних графиков показывает, что по вероятности правильного квантования воздействие помехи с нормальным законом распределения эквивалентно воздействию равномерно распределенной помехи при соотношении .